0358
A group-wise cardiac motion estimation network leveraging temporal correlation1AI in Medicine, Technical University of Munich, Munich, Germany, 2Department of Computing, Imperial College London, London, United Kingdom, 3Medical Image And Data Analysis (MIDAS.lab), University Hospital of Tübingen, Tübingen, Germany
Synopsis
Cardiac motion estimation is the gold-standard for assessing cardiac function and complementing cardiac image reconstruction. However, previous approaches in this area either suffered from long registration times or low accuracy because the inherent temporal correlation of the cardiac motion is not leveraged. In this work, we propose a method called GRAFT, which takes multiple cardiac frames as inputs to leverage the temporal correlation. Furthermore, temporal coherence is ensured by introducing the temporal smoothness loss during the training. Our experiments indicate that GRAFT can provide competitive deformation estimation results to state-of-the-art methods and outperform them in subsequent motion-compensated MRI reconstruction.
Introduction
Cardiac magnetic resonance imaging (CMR) plays an essential role to analyze cardiac morphology and function. Many approaches and tools were developed upon CMR and cardiac motion estimation (CME) is one of the most important and versatile methods among them. In the context of CMR reconstruction, CME can be embedded as a build-in registration function by leveraging the idea of general matrix decomposition1-3. Registration methods like B-splines4,5 or diffusion-based6,7 can serve here as motion estimates for the embedded deformation matrix but they all suffer from long run times. More recently, CME has been reformulated as a learning-based task8-11 whose inference-time is reduced drastically. However, these approaches do not leverage the inherent temporal correlation of the cardiac motion to facilitate the estimation. Furthermore, these methods maximize the CME accuracy only and thus might not fully exploit their potential for downstream tasks like MRI reconstruction.In this work, we introduce a group-wise CME network called GRAFT. GRAFT uses a frame-block mechanism to leverage the temporal correlation of the cardiac images, improving the estimation accuracy. Furthermore, we introduce a temporal smoothness loss term for cyclic-consistent motion, which can be beneficial for downstream cardiac reconstruction tasks. Finally, we train and evaluate our method on in-house acquired 2D CINE data in a self-supervised way. The experiments reveal that GRAFT provides competitive motion estimation accuracy to state-of-the-art methods and outperforms them in motion-compensated reconstruction tasks.
Methods
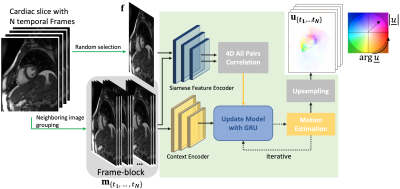
We apply MRAFT12 as our backbone and recast it as a group-wise estimation model, dubbed as GRAFT and illustrated in Fig.1. Instead of just feeding one fixed and one moving image of a cardiac slice into the network, we randomly select one fixed image from the slice, and all $$$N$$$ temporal frames are used as the moving images. We also use the neighboring two frames of the moving image as add-on inputs, which serve as complementary context information for the estimation especially when through-plane-motion is present. This mechanism is denoted as frame-block. Therefore, motion prediction $$$\mathbf{u}_{\{t_1,\cdots,t_N\}}$$$ (with $$$\mathbf{u}=[\mathbf{u}^{(x)},\mathbf{u}^{(y)}]^T$$$) of GRAFT $$$g(\cdot)$$$ can be formulated as$$\mathbf{u}_{\{t_1,\cdots,t_N\}}=g\big(\mathbf{f},\mathbf{m}_{\{t_1,\cdots,t_N\}}\big)$$
where $$$\mathbf{f}$$$ is the randomly selected fixed frame and $$$\mathbf{m}_{\{t_1,\cdots,t_N\}}$$$ contains all moving frames.
Since ground-truth of cardiac deformation is unavailable, GRAFT is trained in a self-supervised manner. Following12, we compose the loss function by a photometric loss with the enhancement mask $$$\Phi$$$ to emphasize the central cardiac region and a spatial smoothness loss to avoid unrealistic flows,
$$\mathcal{L}=\mathcal{L}_{\mathrm{P}}+\beta\mathcal{L}_{\mathrm{S}}=\sum_{t=1}^{N}\sum_{\mathbf{p}\in\Omega}\rho\big(\Phi(\mathbf{p})\cdot(\mathbf{c}_t(\mathbf{p})-\mathbf{f}(\mathbf{p}))\big)+\beta\sum_{t=1}^{N}\sum_{d\in{x,y}}\sum_{\mathbf{p}}\left(|\nabla_d\mathbf{u}_{t}(\mathbf{p})|\right).$$
$$$\mathbf{p}$$$ refers to the 2D image pixels coordinate, $$$\Omega$$$ denotes the image domain, $$$\mathbf{c}_{t}=\mathbf{m}_t(\mathbf{p}+\mathbf{u}_t(\mathbf{p}))$$$ are the motion-corrected images which is warped from $$$\mathbf{m}_t$$$ with the motion fields $$$\mathbf{u}_t$$$ estimated from the network $$$g$$$. $$$\rho$$$ denotes the Charbonnier function13 with $$$\rho(x)=(x^2+10^{-12})^{0.45}$$$.
However, if we also consider the downstream reconstruction task1,16, the above loss terms may not be sufficient as we need to reconstruct the fixed target image from the sum of all motion-corrected images. Therefore, we apply an additional temporal smoothness loss term along the $$$t$$$-axis to emphasize temporal coherence for minimization of the motion estimation gap and avoidance of reconstruction artifacts
$$\mathcal{L}_{\mathrm{T}}=\sum_{t=1}^{N}\sum_{\mathbf{p}}\left(|\nabla_t\mathbf{u}_t(\mathbf{p})|\right)$$
In summary, our total loss function is formulated with hyper-parameters $$$\beta$$$ and $$$\gamma$$$ as
$$\mathcal{L}_{total}=\mathcal{L}_{\mathrm{P}}+\beta\mathcal{L}_{\mathrm{S}}+\gamma\mathcal{L}_{\mathrm{T}}.$$
Experiments
We use in-house acquired short-axis 2D CINE CMR data (17 healthy subjects, 25 patients) for our experiments. Data were acquired with 2D bSSFP (TE/TR=1.06/2.12ms, resolution=1.9$$${\times}$$$1.9mm$$$^2$$$, slice thickness=8mm, 25 temporal phases, 8 breath-holds of 15s duration). We collect 334/20 unique patient slices for training/testing. We train GRAFT with batch size 1 and AdamW14 (learning rate of 1e-4 and weight decay of 1e-5). The hyper-parameters $$$\beta=100$$$ and $$$\gamma=10$$$ were estimated empirically.Regarding the subsequent motion-compensated reconstruction experiments using1,16, we retrospectively undersample the test subjects by $$$R=8$$$ using a VISTA17 sampling.
Results and Discussion
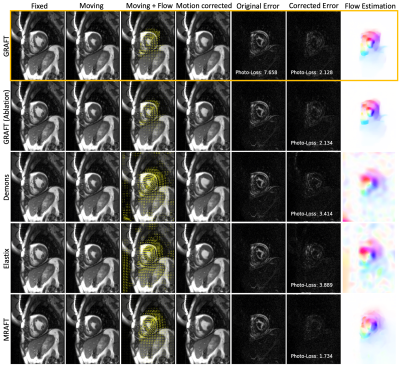
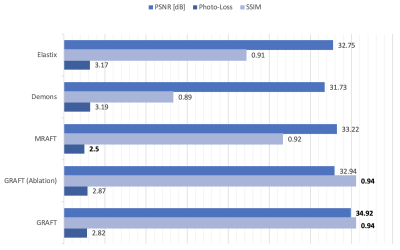
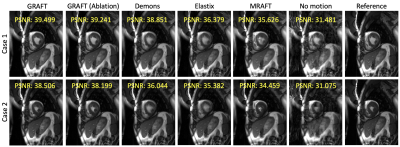
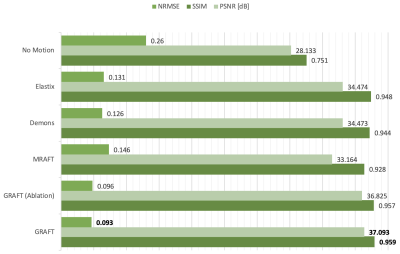
First, we evaluate the motion estimation performance of GRAFT with Demons7, Elastix5, MRAFT12 and GRAFT-Ablation (without frame-block, i.e. using a single moving frame instead of neighboring frames). The qualitative and quantitative results are illustrated in Fig.2 and Fig.3. Although GRAFT is restricted by a temporal constraint during training, it still yields superior results compared to Elastix and Demons and competitive results to MRAFT. Furthermore, the quantitative evaluation reveals that the proposed frame-block can improve the motion estimation accuracy further.Moreover, we perform motion-compensated image reconstruction1,16 involving all 25 temporal frames and use the motion estimation from the above methods as an explicit embedded deformation matrix. Additionally, a reconstruction without motion compensation is executed. The qualitative and quantitative results are shown in Fig.4 and Fig.5. The inferior results of the experiment without a motion model indicate that the registration matrix plays an indispensable role in CMR reconstruction. Furthermore, although MRAFT expresses high motion estimation accuracy, it fails to generate artifact-free reconstructions because no temporal coherence is instilled during training. In contrast, by leveraging the temporal smoothness term and gathering more temporal information using frame-block, GRAFT demonstrates more precise, deblurred, and artifact-free reconstructions.
Conclusion
We propose a CME network called GRAFT, which groups all cardiac temporal frames as network inputs and uses a frame-block to gather more motion information from neighbouring frames. Furthermore, a temporal smoothness loss is introduced in training to ensure temporal cyclic motion coherence. The experiments show that GRAFT provides competitive CME results to state-of-the-art methods and illustrates superior motion-compensated reconstruction performance.Acknowledgements
Thomas Küstner and Kerstin Hammernik contributed equally. This work was supported in part by the European Research Council (Grant Agreement no. 884622).References
[1] Batchelor PG., Atkinson D., Irarrazaval P., Hill DLG., Hajnal J., Larkman D. Matrix description of general motion correction applied to multishot images. Magn Reson Med, 54(5):1273–1280, 2005.
[2] Odille F., Vuissoz PA., Marie, PY., et al., Generalized reconstruction by inversion of coupled systems (GRICS) applied to free‐breathing MRI. Magn Reson Med, 60(1):146-157, 2008.
[3] Bustin A., et al. 3D whole-heart isotropic sub-millimeter resolution coronary magnetic resonance angiography with non-rigid motion-compensated PROST. J Cardiovasc Magn Reson, 22, 24, 2020.
[4] Rueckert D., Sonoda LI., Hayes C., et al. Nonrigid registration using free-form deformations: application to breast MR images. IEEE Trans Med Imaging, 18(8):712-721, 1999.
[5] Klein S., Staring M., Murphy K., Viergever MA., and Pluim JP. Elastix: A toolbox for intensity-based medical image registration. IEEE Trans Med Imaging, 29(1):196–205, 2010.
[6] Thirion J.P. Image matching as a diffusion process: an analogy with Maxwell's demons. Med Image Anal, 2(3):243-260, 1998.
[7] Vercauteren T., Pennec X., Perchant A., Ayache N. Diffeomorphic demons: efficient non-parametric image registration. Neuroimage, 45(1):61–72, 2009.
[8] Qi H., Fuin N., Gruz G., Pan J., Kuestner T, Bustin A., et al. Non-Rigid Respiratory Motion Estimation of Whole-Heart Coronary MR Images Using Unsupervised Deep Learning. IEEE Trans Med Imaging, 41(1):444-454, 2021.
[9] Morales M., Izquierdo-Garcia D., Aganj I., Kalpathy-Cramer J., Rosen B., and Catana C. Implementation and validation of a three-dimensional cardiac motion estimation network. Radiology: Artificial Intelligence, 1(4):e180080, 2019.
[10] Zheng, Q., Delingette, H., Ayache, N. Explainable cardiac pathology classification on cine MRI with motion characterization by semi-supervised learning of apparent flow. Med Image Anal, 56:80–95, 2019.
[11] Yu H., Chen X., Shi H., Chen T., Huang TS., Sun S. Motion Pyramid Networks for Accurate and Efficient Cardiac Motion Estimation. Medical Image Computing and Computer-Assisted Intervention (MICCAI), pp. 436-446, 2020.
[12] Pan J., Rueckert, D., Kuestner T., and Hammernik K. Efficient Image Registration Network for Non-Rigid Cardiac Motion Estimation. MICCAI workshop of Machine Learning for Medical Image Reconstruction. pp 14-24, 2021.
[13] Sun, D., Roth, S., Black, MJ. A quantitative analysis of current practices in optical flow estimation and the principles behind them. Int J Comput Vis, 106(2):115–137, 2014.
[14] Loshchilov, I., Hutter, F.: Decoupled weight decay regularization. arXiv preprint arXiv:1711.05101, 2017.
[15] Zhou W., Bovik AC., Sheikh HR., et al. Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process, 13(4):600-612, 2004.
[16] Pruessmann K., Weiger M., Börnert P., and Boesiger P. Advances in sensitivity encoding with arbitrary k‐space trajectories. Magnetic Resonance in Medicine, pp 638-651, 2001.
[17] Ahmad R., Xue H., Giri S., Ding Y., Craft J., and Simonetti OP. Variable density incoherent spatiotemporal acquisition (VISTA) for highly accelerated cardiac MRI. Magnetic Resonance in Medicine, pp 1266-1278, 2015.
Figures