0354
Spread-Spectrum Modulated Pilot Tone (SSMPT) for Motion Sensing
Daniel Raz Abraham1, Suma Anand1, and Michael Lustig1
1Electrical Engineering and Computer Sciences, University of California, Berkeley, Berkeley, CA, United States
1Electrical Engineering and Computer Sciences, University of California, Berkeley, Berkeley, CA, United States
Synopsis
Pilot Tone (PT) navigators are tones within the MR receiver bandwidth that are used to estimate subject motion. However, the PT must be placed outside the imaging band. This is not always feasible for all types of imaging (e.g. spine imaging) and systems, since the PT may overlap with the image. In this work, we propose Spread-Spectrum Modulated Pilot Tone (SSMPT), which spreads the energy of the pilot tone over the entire imaging band. SSMPT produces comparable motion estimates to PT and respiratory bellows, as demonstrated in a free-breathing scan with a healthy volunteer.
Introduction
In MRI, motion sensing plays a crucial part in obtaining clean images that are robust to physiological motion. Conventional motion sensing requires sequence dependent solutions (e.g., navigators) or sensors on the subject (e.g., bellows). The Pilot Tone (PT) navigator has been established as a promising alternative1-4. PTs are pure tones within the MR bandwidth that are modulated by patient motion and received by the receiver coils. However, the PT must be placed outside the imaging band, which requires knowledge of the MR bandwidth and center frequency. For that reason, PT is not always feasible or convenient. In this work, we overcome this limitation by spreading the energy of the PT over a larger bandwidth. Our proposed method, the Spread Spectrum Modulated Pilot Tone (SSMPT), adds a small amount of noise to the entire imaging band which can then be estimated and removed from the image while remaining robust to changes in MR parameters.Methods
MotivationThis methodology is motivated by the Direct Sequence Spread Spectrum (DSSS) where a pure tone is spread over many frequencies by multiplying the tone with a pseudo-random sequence (PRS) of +1 and -1. The PRS is chosen because its autocorrelation looks like a scaled discrete-time delta function, which is useful for demodulation, and because the spectrum of the PRS is evenly spread out over a large bandwidth. This yields a noise-like artifact rather than a zipper artifact that appears in PT (Figure 1). A spread spectrum allows the SSMPT to remain robust to MR parameters such as bandwidth and center frequency.
Model
A PRS $$$R[n]$$$ of length $$$M$$$ is transmitted repeatedly during the acquisition. Each received k-space readout can be written as $$y[n] = k[n] + AR_N[n-d]$$where $$$y[n]$$$ is the received readout, $$$k[n]$$$ is the unmodulated k-space line of length $$$N$$$, $$$A$$$ is the amplitude of the motion signal that we wish to recover, and $$$R_N[n-d]$$$ is the true PRS shifted by $$$d$$$ samples and truncated to be of length $$$N << M$$$. $$$k[n]$$$ and $$$d$$$ are unknown. We recover the desired quantity $$$A$$$ by cross-correlating each received line $$$y[n]$$$ with the PRS and taking the maximum value,$$ A \approx \max_n \frac{1}{N} R[n] \star y[n] $$ where $$$\star$$$ denotes cross-correlation. Because the sequence $$$R[n]$$$ is a PRS, and thus has desirable autocorrelation properties, we assume that $$$ R[n] \star R[n -d ] \approx M\delta[n - d]$$$ and $$$R[n] \star k[n] \approx 0$$$. However, in practice, the variation in $$$k[n]$$$ is large at the center of k-space, which violates this assumption. In order to combat this, we remove the peak by interpolating the problematic motion estimate points with a degree 10 polynomial. Finally, the motion estimate is lowpass filtered and is used to subtract the SSMPT noise to obtain a clean, corrected image. Figure 2 describes this pipeline in detail.
Simulation
The SSMPT technique was verified in simulation using a 2-D Cartesian k-space acquisition. For each k-space line, the SSM-PT was added with a random phase to emulate the scanner environment. To simulate respiratory motion, the SSMPT was amplitude modulated with a frequency of 0.3Hz. Figures 3b) and 3e) show that a weaker SSMPT causes a very large error in the motion estimate at the center of k-space, and that a stronger SSMPT gives a better motion estimate. Figures 3c) and 3f) show that the SSMPT removal process performs well but yields small streak-like artifacts due to discrepancies between the motion estimate and the true motion.
Results
AcquisitionTo test the SSMPT technique in-vivo, images were acquired on a GE 3T MR750W system with a healthy volunteer. A software-defined radio (USRP-B200, National Instruments, TX, USA) was used to transmit the SSMPT. A single-slice, free-breathing abdominal SSFP scan (FA=35, TR=4.4ms, resolution=1.9mm) was acquired using SSMPT, conventional PT, and the bellows for respiratory sensing. The antenna was placed on top of the 32-channel combined anterior and posterior coil array.
Motion Estimation
The SSMPT is compared against the standard PT. Both are transmitted at the same transmit power. Images were reconstructed using a sum of squares on all but 4 coils due to noise. From Figures 4b) and 4e), we see that the SSMPT is comparable to the PT in measuring respiratory signals. After removing the SSMPT from the image, Figure 4f) shows that just a small amount of the noise persists.
In Figure 5, we derive motion estimates from the SSMPT under different transmit strengths. All the motion estimates perform well in comparison to the bellows signal. Figures 5d) and f) show the images after noise removal. Under a lower transmit gain, the recovered image quality is improved.
Conclusion
SSMPT spreads a pure tone over the entire imaging band. This allows SSMPT to remain more robust to changes in MR sequence parameters. The SSMPT noise artifact can be estimated and removed, preserving image quality. Simulated and in-vivo results suggest that SSMPT is comparable to the standard PT and Bellows for motion estimation while being more flexible for practical use.Acknowledgements
We thank Alan Dong for his insights and useful discussions on Spread Spectrum Modulation.References
- Falcão, M. B., Di Sopra, L., Ma, L., Bacher, M., Yerly, J., Speier, P., ... & Roy, C. W. (2021). Pilot tone navigation for respiratory and cardiac motion‐resolved free‐running 5D flow MRI. Magnetic resonance in medicine.
- Vahle, T., Bacher, M., Rigie, D., Fenchel, M., Speier, P., Bollenbeck, J., ... & Boada, F. E. (2020). Respiratory Motion Detection and Correction for MR Using the Pilot Tone: Applications for MR and Simultaneous PET/MR Exams. Investigative radiology, 55(3), 153.
- Ludwig J, Speier P, Seifert F, Schaeffter T, Kolbitsch C. Pilot tone-based motion correction for prospective respiratory compensated cardiac cine MRI. Magn Reson Med. 2021.
- Solomon E, Rigie DS, Vahle T, Paska J, Bollenbeck J, Sodickson DK, et al. Free-breathing radial imaging using a pilot-tone radiofrequency transmitter for detection of respiratory motion. Magn Reson Med. 2021.
Figures
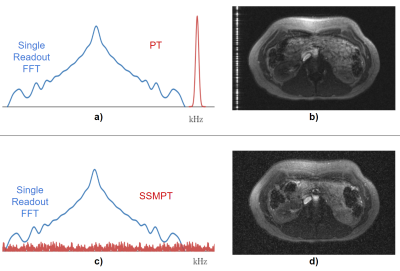
Figure 1: a) Fourier transform (single readout) for the conventional Pilot Tone (PT) acquisition with b) the corresponding artifact, which appears as a line in the image. c) Fourier transform (single readout) for the SSMPT acquisition with d) the corresponding artifact, which is noise-like and spread over the entire image..
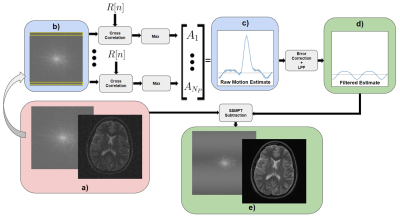
Figure 2: The SSMPT acquisition setup: a)The input is a k-space frame, from which we b) extract one readout at a time to derive the motion estimate using cross correlation. c) The raw motion estimate is then d) filtered and used to subtract the SSMPT from the original data to get e) a less-noisy image. The images in this pipeline are from simulated data. $$$N_P$$$ is the number of phase encodes.
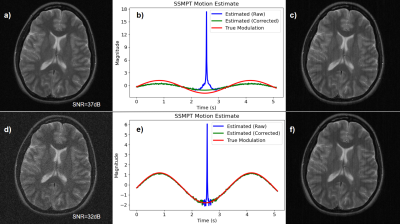
Figure 3: a) A weak SSMPT with image SNR of 37dB (we treat the SSMPT as noise) is used to determine b) the motion estimate which is then peak-corrected. The corrected estimate is used to c) subtract the SSMPT from the original data. This process is repeated for a stronger SSMPT with SNR of 32dB in figures d), e), f).
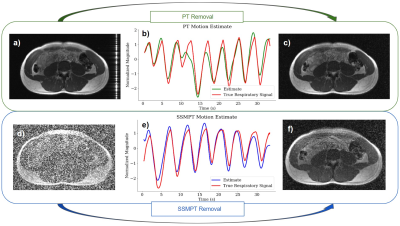
Figure 4: PT is compared against SSMPT at the same transmission power. a) The standard PT is applied to an abdominal scan, then b) a motion estimate is derived. c) We filter out the pilot tone after motion estimation. d) SSMPT is applied to an abdominal scan, then e) the motion estimate is derived using the process described in Figure 2. We use the estimate to f) filter out the SSMPT noise from the image. (The true respiratory signal is from the bellows).
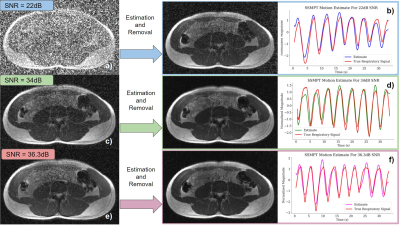
Figure 5: The SSMPT removal is shown for different transmit gains. Each one results in a different image SNR. The SSMPT is activated during a scan yielding a) an SNR of 22dB. b) (right) The motion estimate in blue is compared against the true respiratory signal in red. (left) SSMPT is removed from the image. Process is repeated for c) - d) with an SNR of 34dB and e) - f) with an SNR of 36.3dB. (The true respiratory signal is from the bellows).
DOI: https://doi.org/10.58530/2022/0354