0353
Prospective Head Motion Correction Using Orbital K-Space Navigators and a Linear Perturbation Model1Institute for Biomedical Engineering, ETH Zurich and University of Zurich, Zurich, Switzerland
Synopsis
It has
recently been proposed to estimate head motion from orbital k-space navigators
based on a linear signal model of the complex-valued navigator signal. In this
work, we describe the combination of this algorithm with prospective motion
correction, forming a control circuit that tracks the head so that the linear
model remains valid also for large motion ranges. This ability is demonstrated by
implementation and in-vivo imaging at 7T.
Introduction
Head motion is a frequent problem in brain MRI that causes image artifacts and often necessitates rescans in the clinical setting. Motion correction, prospectively or retrospectively, is typically based on tracking the head while scanning. Among various approaches for motion tracking1,2, k-space navigators have the advantage that they work without any additional hardware, relying on MR signal from the head itself.For fast estimation of head motion from short navigators, it has been proposed to analyze them in terms of linear perturbation of the complex-valued navigator signal3. Based on simple least-squares fitting, this approach has low computational cost and requires minimal reference data. However, its range of validity is limited by the underlying linear approximation. In this work, we address this limitation by prospective motion correction (PMC) based on the linear estimates, forming a control circuit in which the linear model remains valid by keeping its reference point stable in the head frame of reference. We demonstrate this ability by implementation and in-vivo imaging at 7T.
Methods
The proposed technique was implemented on a whole body 7T MRI system (Philips Achieva). A single-shot orbital navigator4 with a k-space radius of 400 rad/m was inserted into a 3D gradient-echo sequence as shown in Figures 1 and 2. During every TR, the navigator signal is acquired and forwarded to a host computer via TCP connection.For each TR, once the navigator signal arrives, the increment in head motion since the last geometry update is calculated by linear least-squares fitting, as described in Ref. (3), implemented in C++ for fast computation. Specifically, the rigid-body motion parameters (3 rotations, 3 translations) are fitted to the change in complex-valued navigator signal relative to an initial reference navigator. The results are then fed back to the console for PMC, i.e., corresponding incremental rotation of navigator and imaging gradients as well as modulation and demodulation of RF pulses and received signals, respectively, according to net translation.
For in-vivo demonstration, the 3D sequence was carried out with TE=15.79ms, TR=41.8ms, flip angle=18°, resolution=1x1x2 mm³, FOV=190x150x100 mm³, scan duration = 5:06 minutes, using a 32-channel head receive array. With these parameters, the latency of PMC was up to 250 ms. A healthy volunteer was instructed either to stay still or to perform a single and steady, small or large head motion after half the scan duration. The volunteer was asked to reproduce these motions as accurately as possible. The scans with intentional motion were performed with and without PMC.
Results
Figure 3 shows the tracking and imaging results obtained with no intentional motion and with moderate intentional motion, amounting to up to 2.8 mm of translation and 2.4 degrees of rotation. Without intentional motion, the tracking results show typical slow drift along with oscillation due to breathing. These excursions are small at the scale defined by the navigator radius of 400 rad/m so that the linear model remained valid even without PMC. Intentional motion resulted in palpable artefact, which was successfully removed by PMC, achieving very similar quality as when the volunteer held still. Remaining artefact in the lowest slice is due to through-plane dephasing as also seen without intentional motion.Figure 4 shows the results obtained with strong intentional motion. At large excursions up to 5.8 degrees and 5 mm, PMC still achieved substantial correction relative to the uncorrected case. Remaining artefact is most pronounced around the circumference of the brain while some fine details such as the central fissure and radial veins are still recovered. The time courses of the motion are plausible for the requested manoeuver. Conversely, without PMC, the image results are strongly impaired and the motion parameters are implausible, reaching much smaller excursions and suggesting, e.g, abrupt forth-and-back y rotation clearly inconsistent with the volunteer instructions.
Discussion
These results indicate that the proposed approach was effective at detecting and correcting for moderate head motion of up to 3 degrees and millimeters. With strong head motion, it still improved image quality substantially, indicating that motion tracking per se still worked quite accurately. This is consistent with plausible time courses of the recorded motion parameters and suggests that feedback control of the reference point indeed rendered the linear expansion valid across a large motion range. It doing so, the linear model estimates only the motion increment since the latest geometry update. In contrast, without PMC and thus without control of the reference point, the linear fit estimates net motion and the tracking failed due to excessive violation of the linear picture.Although PMC permitted the detection of large motion, it did not fully recover image quality in the strong-motion case. Artefacts remained particularly around the circumference of the head, which could relate to secondary motion effects that cannot be corrected by mere geometry update. Possible mechanisms include change in coil sensitivities in the head frame of reference and motion-induced B0 perturbation.
Conclusion
This study suggests that navigators as brief as 2-3 ms, in conjunction with PMC and a linear perturbation model, permit effective motion tracking for 3D imaging with simple, fast run-time computation and minimal demand for reference information.Acknowledgements
No acknowledgement found.References
- Godenschweger, F. et al. Motion correction in MRI of the brain. Phys. Med. Biol. 61, R32 (2016).
- Maclaren, J., Herbst, M., Speck, O. & Zaitsev, M. Prospective motion correction in brain imaging: A review. Magnetic Resonance in Medicine 69, 621–636 (2013).
- Ulrich, T. & Pruessmann, K. P. Detection of Head Motion using Navigators and a Linear Perturbation Model. ISMRM & SMRT Virtual Conference & Exhibition (2021).
- Ulrich, T., Patzig, F., Wilm, B. J. & Pruessmann, K. P. Towards Optimal Design of Orbital K-Space Navigators for 3D Rigid-Body Motion Estimation. ISMRM & SMRT Virtual Conference & Exhibition (2020).
Figures

Sequence diagram of the imaging sequence including the navigator gradients. The navigator was inserted into a 3D gradient echo sequence after the slab-selective RF excitation and before the phase encoding and imaging gradients.
Since there is significant dead time between the excitation and the imaging readout, the navigators can be inserted without increasing scan time.
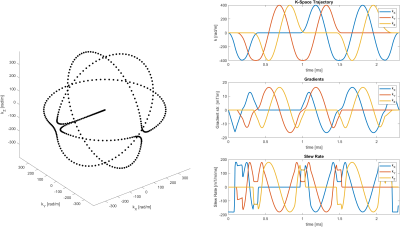
Orbital navigator k-space trajectory. Left: Parametric plot of the trajectory shape. Right: Plots of the trajectory, gradients, and slew rate over time. The trajectory is made up of three orthogonal circles, with smooth transitions in between them. At a radius of 400 rad/m, the navigator signal can be acquired in 2.3 milliseconds.
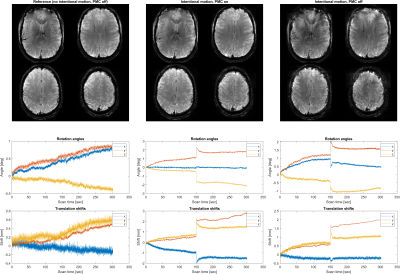
Images and motion parameters for the imaging experiment, where the volunteer was instructed to perform a moderate rotation and translation after half the scan duration. The estimated rotation angles and translational shifts are in the range of up to 2.8 mm and 2.4 degrees.
Left column: Reference image without intentional motion and without motion correction;
Middle column: Image with intentional motion and with PMC;
Right column: Image with intentional motion and without PMC
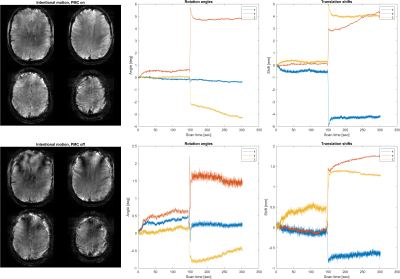
Images and motion parameters for the imaging experiment, where the volunteer was instructed to perform a large rotation and translation after half the scan duration. The estimated rotation angles and translational shifts are in the range of up to 5 mm and 5.8 degrees.
Upper row: PMC on, bottom row: PMC off