Introduction

Many motion correction algorithms have been proposed to allow for the clinical interpretation and quantitative analysis of motion-corrupted magnetic resonance images (MRI)¹. Among these algorithms, the trimmed autocalibrating k-space estimation based on structured matrix completion (TAKE) algorithm² was proposed to retrospectively correct raw k-space data collected with 2D MR sequences without requiring an additional navigator in the pulse sequence. Two major limitations prevent the use of TAKE in clinical practice: 1) the detection of motion-corrupted k-space lines depends on the local k-space energy, thus leading to both the non-detection of low energy motion-corrupted lines and false detection of non-corrupted lines characterized by a high energy; and 2) the computation time is prohibitive to allow for the algorithm to be used in a standard clinical workflow. In this context, the current study aims at providing a robust version of TAKE (Robust TAKE) characterized by both a lower dependency to the local k-space energy and a shorter computation time.

Methods

TAKE consists in detecting motion-corrupted k-space lines from residuals computed between the raw k-space data and its structured low rank matrix approximation². In TAKE, the motion detection was reduced to a 1D problem by summing the residuals in the frequency encoding (FE) and coil dimensions. Raw k-space phase encoding (PE) lines with the maximum residual value were iteratively detected as motion-corrupted and replaced by their approximation until all 1D residual robust z-scores were lower than a given threshold.
The improvements proposed in Robust TAKE compared to TAKE are the following: the raw k-space was subject to coil compression to decrease the computation time; the 2D kernel used for structured low rank matrix approximations was replaced by a 1D kernel in the PE dimension; the residuals were computed with the Berhu norm³ instead of the L1 norm; robust z-scores (denoted as energy dependent z-scores) were computed on the residuals as a function of the k-space center distance in order to reduce the local k-space energy dependency; the k-space was linearly subsampled in the FE dimension by a factor equals to twofold the PE subsampling rate in order to both reduce the local energy dependency and computation time; the 1D residuals were obtained by summing the energy dependent z-scores in the coil dimension and then computing their median in the FE dimension; and the motion corrupted k-space lines were replaced by their SPIRIT approximation⁴ instead of their structured low rank matrix approximation.
In-vivo MR experiments were conducted under written informed consent on a 3T system (MAGNETOM Vida, Siemens Healthcare, Erlangen, Germany) using a 20-channel head and neck coil. Raw k-space data was collected on two healthy volunteers that underwent T2-weighted turbo spin echo imaging (40 slices; resolution: 0.5 x 0.5 x 3 mm³; GRAPPA 2; TA: 2:52 mins) in two different head positions. Motion-corrupted Monte-Carlo experiments were generated by randomly replacing 5% of PE lines from one T2-weighted k-space data by their counterparts in the second T2-weighted k-space data (10 experiments per slice). Experiments from three randomly selected slices of the same subject were used as a training database to optimize kernel sizes and 1D residual z-score thresholds. The remaining experiments were used as a validation database on which the motion detection sensitivity and specificity were computed. The gradient entropy, a metric that was strongly related to observer ratings of MRI motion corruption in a previous study⁵, was computed on the TAKE and Robust TAKE reconstructed MR images and compared with the ground truth to assess the algorithms motion correction performances.

Results

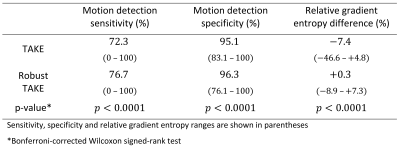
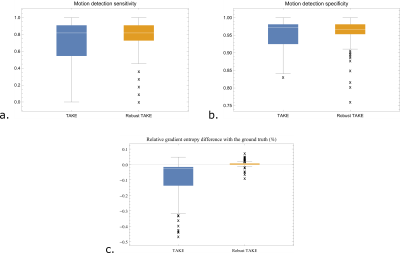
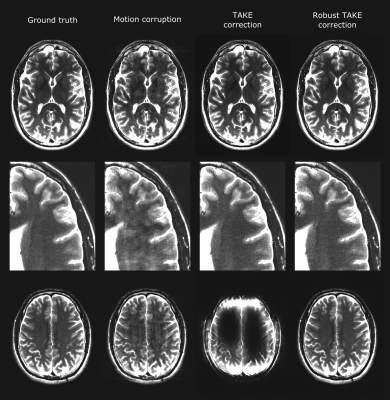
The energy dependent z-scores used by Robust TAKE for motion detection showed a lower dependence to the local k-space energy than the residuals used by TAKE (Figure 1). The local k-space energy dependency remained lower in Robust TAKE when the motion detection was reduced to a 1D problem (Figure 2). The Robust TAKE lower k-space energy dependency allowed to significantly improve its motion detection sensitivity (76.7% vs 72.3%, p<0.0001) and specificity (96.3% vs 95.1%, p<0.0001) compared to TAKE (Table1, Figure 3). Similarly, the motion correction performances provided by Robust TAKE were significantly better (p<0.0001) than the ones provided by TAKE (Table 1, Figure 3).
In most cases, TAKE and Robust TAKE greatly reduced the presence of motion artefacts in reconstructed images (Figure 4, top rows). However, the TAKE reconstruction sometimes failed due to the false rejection of too many lines characterized by a high energy (Figure 4, bottom row). The TAKE and Robust TAKE performances can also greatly decrease for cases where the motion detection threshold is incoherent with the data, which either leads to a very low sensitivity or lowers the specificity.
The average Robust TAKE computation time (21 secs) was 97% lower than the average TAKE computation time (673 secs).

Discussion

Robust TAKE allowed to significantly improve both motion detection and correction performances compared to TAKE, while greatly reducing the algorithm computation time to reach performances more suitable for a clinical routine use. However, the Robust TAKE performances greatly decrease when the motion detection threshold is incoherent with the data. Future studies will aim at further improving the Robust TAKE performances by using adaptive motion detection methods with data-driven threshold definitions.

Acknowledgements

This project is supported by Siemens Healthcare SAS, France and Aix-Marseille University around the industrial Chaire 7TEAMS