0316
Advanced Gradient-Free Selective Excitation Using the Bloch-Siegert Shift
Jonathan B Martin1, Sai Abitha Srinivas1, Christopher Vaughn1, Heng Sun1, Mark Griswold2,3, and William Grissom1,4
1Biomedical Engineering, Vanderbilt University, Nashville, TN, United States, 2Department of Radiology, Case Western Reserve University, Cleveland, OH, United States, 3Biomedical Engineering, Case Western Reserve University, Cleveland, OH, United States, 4Electrical Engineering, Vanderbilt University, Nashville, TN, United States
1Biomedical Engineering, Vanderbilt University, Nashville, TN, United States, 2Department of Radiology, Case Western Reserve University, Cleveland, OH, United States, 3Biomedical Engineering, Case Western Reserve University, Cleveland, OH, United States, 4Electrical Engineering, Vanderbilt University, Nashville, TN, United States
Synopsis
A class of selective RF pulses which use the Bloch-Siegert shift to localize selective excitation without B0 gradients has recently been proposed. Here we report an improved design method for both the frequency-gradient inducing component pulse and the frequency-selective component pulse, which reduces ripple in the magnetization profile and produces flatter passbands across the excited B1+ range. The pulses’ production of multiphoton resonances across B1+ and their suitability for fast gradient-free CPMG imaging are investigated. They are deployed for the first time on a low-field scanner to produce slice-selective selection.
Introduction
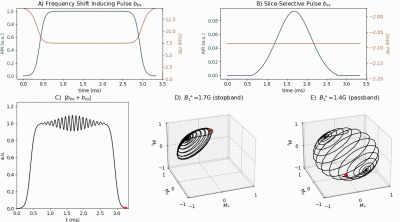
A method for B0-gradient-free selective excitation pulses using the Bloch-Siegert shift was recently proposed1 which sums an off-resonant RF pulse bbs that produces a frequency gradient in B1+ via the Bloch-Siegert shift and a frequency-selective pulse bss that produces excitation across a desired B1+ range (Fig.1). However, the original Bloch-Siegert selective excitation (BSSE) pulses had excessive ripple from out-of-band excitation, and struggled to produce a flat profile across varying B1+. We propose an improved bbs pulse using a Fermi AM envelope with adiabatic frequency sweeps to mitigate extraneous excitation, and a modified SLR filter design method that compensates for varying B1+. Subsidiary multiphoton resonances produced by BSSE pulses are characterized and their distribution in B1+ predicted. With these improvements, simulations show that BSSE pulses can control signal phase for B0-gradient-free CPMG imaging. The pulses were finally deployed on a 47.5mT scanner with inhomogeneous B1+, the first use of these pulses for spatially selective excitation.Pulse Design Improvements
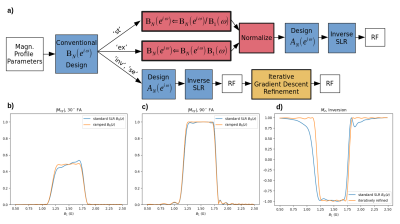
A previous limitation of BSSE pulses was how close the off-resonant bbs be brought to the Larmor frequency without producing out-of-band excitation. Smaller offsets allow for shorter duration pulses. Offsets can be reduced without producing unwanted excitation by means of adiabatic sweeps to and from the offset2. In this improved pulse design, a Fermi A(t) envelope is used, with symmetric time-varying frequency offset given by:$$\omega_{rf}(t)=\frac{\gamma A(t)}{\sqrt{(1-\frac{\gamma A(t)}{K}t)^{-2}-1}},\hspace{0.25cm}t=0:T/2$$which is modified here to accommodate time-varying A(t) 2. For all pulses considered, K=0.2. The effect of these adiabatic frequency sweeps is shown in Fig.1. The initial adiabatic component of the pulse produces a constant rotation across B1+ in the ⍵off rotating frame to a tilted B1,effective axis. Following a B1+-dependent nutation, the second adiabatic frequency sweep brings both the in-band and out-of-band magnetization back to alignment with B0.An improved method from producing flat excitation across B1+ is outlined in Fig.2a. In the case of a small-tip or 90° excitation, a flat passband is produced by scaling the BN(exp(i⍵) profile of the SLR frequency-selective pulse by the corresponding B1+(⍵) predicted by the Bloch-Siegert shift, $$$B_1^+(\omega)\approx\sqrt{2\omega_{off}\omega}/\gamma$$$. In the case of 180° pulses this scaling is not applicable. However, autodifferentiated iterative gradient descent optimization of the RF pulse with respect to its' magnetization profile can refine the pulse to produce the desired profile (Fig.2d).
Multiphoton Resonances
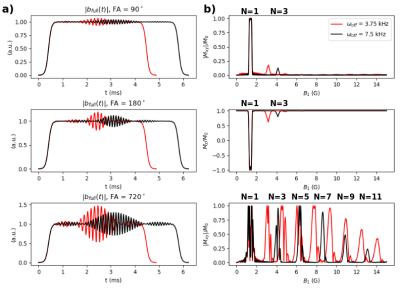
Mixing of the simultaneously applied bbs and bss produces multiphoton resonances3. These are distributed across frequency and thus across B1+ as shown in Fig.3. From the Bloch-Siegert shift relationship without large-offset approximation4 and the multiphoton resonance conditions5, the Nth resonance in B1+ occurs at:$$B_{1, mp}^+(N,\omega_{av},\omega_{off})\approx\frac{\omega_{off}}{\gamma}\sqrt{\Big(1+\frac{N|\omega_{off}-\omega_{av}|-\omega_{av}}{\omega_{off}}\Big)^2-1},\hspace{0.25cm}N=1,3,5,...$$where $$$\omega_{av}=(\omega_{ex}+\omega_{off})/2$$$ and here ⍵off>0, ⍵ex<0. Increasing ⍵off shifts multiphoton resonances upward in B1+, allowing them to be moved from the ROI at the cost of increased pulse duration.Methods
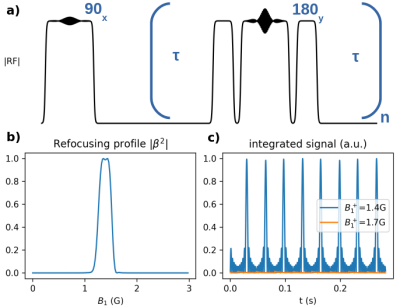
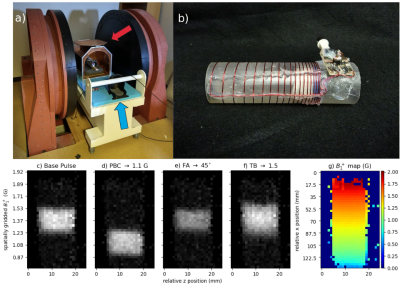
A B0 -gradient-free multi-echo spin-echo sequence was simulated using BSSE pulses to demonstrate their suitability for sequences requiring phase control. Excitation and refocusing pulses with passband center (PBC)=1.4G, passband width (PBW)=0.3G, time-bandwidth product (TB)=4, ⍵off=7.5kHz, T=6.22ms were designed. They were simulated across off-resonance in an 8-echo pulse sequence with τ=35 ms, T1=T2=∞. For rephasing gradients, a BSSE pulse with bss=0 and Kbs=-0.5Kbs,inversion was used, which produced a frequency shift without excitation. The 90° excitation pulse from the CPMG simulation was then deployed in a 3D-GRE sequence (TR/TE=27/425ms, dx/dy/dz=2.0/3.5/3.5mm, 5 averages) on a 47.5mT permanent-magnet scanner using a variable-pitch T/R solenoid coil with spatially inhomogeneous B1+. A 50 mL 1mM CuSO4 tube phantom was imaged. The acquisition was repeated three times with one parameter of the excitation pulse changed in each acquisition: PBC decreased to 1.1G, FA decreased to 45°, and TB decreased to 1.5. To generate a B1+ map by the Bloch-Siegert method6, the same base 3D-GRE sequence was used with the addition of crushers and a hard pulse excitation, and with the BSSE pulse's bss = 0.Results
Fig.2 shows the result of analytic BN(exp(i⍵)) correction (b-c) and iterative refinement of an inversion pulse (d). Profile slope was removed in Fig.2b and profile ripple is flattened in Fig.2c. Iterative optimization improved the inversion’s transition regions to within design specifications in Fig.2d. Fig.4 shows the results of the CPMG sequence simulation. The inversion pulse had highly selective refocusing efficiency in B1+ resulting in a train of echos with variation in echo magnitude <1.5% produced from the passband but little stopband signal. Fig.5 shows the results of the scanner experiments. Shifting the designed PBC from 1.4G to 1.1G shifted the profile by approximately 0.3G, reducing FA to 45° reduced mean slice signal by 63%, and decreasing TB to 1.5 broadened the transition regions corresponding to the modified pulse's reduced selectivity.Discussion and Conclusion
An improved design of BSSE pulses was described with adiabatic sweeps and B1+ ramp compensation across the passband. Multiphoton excitations produced by the pulses were characterized, and the pulses were validated in a CPMG Bloch simulation and an imaging experiment at 47.5mT. Out-of-band excitation and sloped excitation across the passband were resolved by analytic (for FA up to 90°) or iterative means (for 180° pulses). Multiphoton resonances can be predicted and shifted out of the ROI. Results showed that pulses can be used for several applications including slice-selection in RF-encoded MRI and RF-encoded RARE imaging.Acknowledgements
This work was supported by NIH grants R01 EB 030414 and R01 EB 016695. The authors thank Benjamin Hardy for helpful conversations.References
1. Martin J, Vaughn C, Griswold M, Grissom W. Bloch-Siegert |B1+|-Selective Excitation Pulses, Proc. Intl. Soc. Mag. Reson. Med. (2021). p 1911.
2. Khaligi M, Rutt B, Kerr A. Adiabatic RF Pulse Design for Bloch-Siegert B1+ Mapping. Magn. Reson. in Med. 2013; 70(3):829–835.
3. Zur Y, Levitt M H, Vega S. Multiphoton NMR spectroscopy on a spin system with I=1/2. J. Chem. Phys. 1983; 78(9):5293-5310.
4. Ramsey N. Resonance Transitions Induced by Perturbations at Two or More Different Frequencies. Phys. Rev. 1955; 100(4):1191-1194.
5. Krauss E, Vega S. Four-field excitation of multiphoton NMR resonances in spin I=1/2. Phys. Rev. A. 1986; 34(1):333-350.
6. Sacolick L, Wiesinger F, Hancu I, Vogel M. B1 mapping by Bloch-Siegert shift. Magn. Reson. in Med. 2010; 63(5):1315-1322.
Figures
Figure 1) (Animated-click to play) a) Fermi pulse with adiabatic frequency sweeps used for bbs b) frequency-selective pulse bss. This pulse has constant FM to excite a fixed range of B1+ c) Magnitude envelope of a BSSE inversion pulse. d) Motion of the normalized magnetization vector in the frame rotating at ⍵off, for an isochromat in the stopband of the inversion pulse. By the end of the pulse, magnetization is essentially unperturbed. Red trace is 100 µs. e) Magnetization motion for an isochromat in the passband of the pulse. By the end of the pulse, magnetization is fully inverted.
Figure 2) a) Modified SLR design algorithm to compensate for a sloped excitation profile across B1+. In the case of small-tip ('st') or 90° ('ex') excitation, a pointwise scaling of the BN(exp(i⍵)) profile is sufficient. In the case of an inversion/refocusing pulse, iterative refinement is required. b) Uncorrected and corrected 30° excitation, c) Uncorrected and corrected 90° excitation, d) Uncorrected and corrected inversion profile after 50 iterations of autodifferentiated gradient descent optimization of the pulse with respect to its magnetization profile.
Figure 3) a) 90°, 180°, and 720° excitation pulses, with frequency offsets of 3.75 kHz (red) and 7.5 kHz (black). Increasing the offset increases pulse duration. b) However, increasing the offset also pushes multiphoton (N≥3) resonances up in B1+. Multiphoton resonances beyond N=3 are indistinguishable from profile ripple unless the excitation flip angle is increased dramatically. For the 7.5 kHz (black) pulse, N=1 through N=11 resonances are predicted to occur at B1+mp= [1.40, 4.14, 6.52, 8.83, 11.11, 13.38] G. All resonances are at the predicted locations in B1+.
Figure 4) a) CPMG pulse sequence RF. A 90° excitation is followed by a train of 180° refocusing pulses, with RF rephasing gradients which rewind phase using the Bloch-Siegert shift. b) |β2| Refocusing profile for the refocusing pulse (PBC=1.4G, PBW=0.3G). The refocusing was highly selective. c) Signal timecourse integrated across off-resonance for an isochromat in the passband and in the stopband.
Figure 5) a) 47.5mT permanent magnet scanner used for experiment. A Faraday cage (red arrow) and a noise pickup coil (blue arrow) are used to mitigate EMI. b) Inhomogeneous variable-pitch T/R solenoid coil used for imaging. Tube phantom is inside of the coil. c) Excitation produced by a 90°, PBC=1.4G, TB=4 base pulse, d) PBC decreased to 1.1G; slice shifts downward in B1+ by approximately 0.3G e) FA decreased to 45°; mean slice signal decreases to 63% that produced by base pulse f) TB decreased to 1.5; the profile's transitions become broader. g) B1+ map acquired by the Bloch-Siegert method.
DOI: https://doi.org/10.58530/2022/0316