0300

Through-plane diffusion MRI super-resolution with autoencoders: validation on outlier replacement scheme for pre-term baby brains
Hamza Kebiri1,2, Erick J. Canales-Rodríguez3, Priscille de Dumast1,2, Athena Taymourtash4, Hélène Lajous1,2, Yasser Alemán-Gómez2, Georg Langs4, and Meritxell Bach Cuadra1,2,3
1CIBM Center for Biomedical Imaging, Lausanne, Switzerland, 2Department of Radiology, Lausanne University Hospital and University of Lausanne, Lausanne, Switzerland, 3Signal Processing Laboratory 5 (LTS5), Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland, 4Computational Imaging Research Lab, Department of Biomedical Imaging and Image-guided Therapy, Medical University of Vienna, Vienna, Austria

Synopsis

Although super-resolution diffusion MRI for isotropic volumes has been explored, to date no unsupervised SR techniques have been investigated for anisotropic dMRI. We propose an autoencoder based framework to enhance the through-plane spatial resolution and to replace slice outliers by leveraging existing high-quality datasets. Quantitative evaluation on 31 pre-term subjects show that the proposed framework significantly outperforms conventionally used interpolation methods at the raw data and estimated diffusion tensor maps. This can hence contribute to the depiction of more accurate white matter properties of the developing brain.

Introduction

Diffusion Magnetic Resonance Imaging (dMRI) has been the cornerstone for in vivo non-invasive white matter investigation with a high potential for studying the developing brain1, particularly for early stages of development (e.g. neonates and pre-term babies). Unpredictable movements and the low signal-to-noise ratio, which is inherently limited by the small brain size, result in reduced spatial resolution and often slice corruption2 that further affect subsequent processing steps. To overcome the low spatial resolution, interpolation is often used, and has proven useful for diffusion tensor maps and tractography enhancement3. Recently, super-resolution methods using supervised learning4,5,6,7 have been proposed. These approaches need high-resolution training datasets, which are often limited for the developing brain, and focus on further enhancing 3D image resolution but were not evaluated in anisotropic settings. In fact, through-plane dMRI enhancement is needed when highly corrupted slices are discarded8,9 (outlier rejection) or in some applications such as fetal imaging, where 2D thick slice acquisitions are necessary to deal with unexpected motion. In this work, we focus on the former, where, to our knowledge only interpolation approaches have been proposed10. Inspired by previous works on cardiac T2-weighted MRI11, we present an autoencoder framework to increase the through-plane resolution of dMRI. Autoencoders (AEs) are neural networks that learn in an unsupervised way to encode sufficient data representations and can behave as generative models if this representation is structured enough. We demonstrate their practical value for through-plane super-resolution in the context of replacing corrupted slices in pre-term brain dMRI.

Methodology

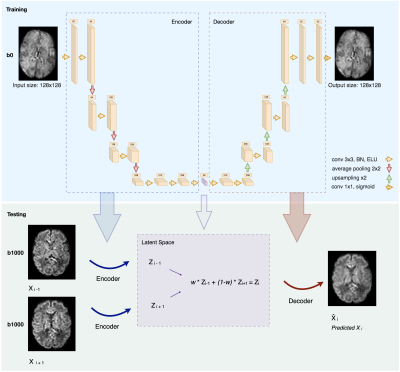
Dataset. Our data come from the developing Human Connectome Project (dHCP). Acquisitions were performed using a Philips Achieva scanner (32-channel neonatal head-coil) with a monopolar spin-echo echo-planar imaging Stejksal-Tanner sequence (Delta= 42.5 ms,  delta=14 ms, TR=3800 ms, TE=90 ms). The final resolution is 1.17 x 1.17 x 1.5 mm3. A multishell (b in {0,400,1000,2600} s/mm2) sequence with 300 volumes was used. We extracted 31 subjects from the pre-term cohort (≤37 gestational weeks) in the range [29.3; 37.0]. Brain masks and region labels were available in the corresponding anatomical dataset.
Network & training. Inspired by Sander et al.11, our network architecture is described in Figure 1. We have used 8-fold nested cross-validation where we trained and validated on 27 subjects and tested on 4. The network was trained on 25,920 2D axial slices from the non-diffusion weighted images (b0) for 200 epochs using Adam optimizer12. The number of feature maps of the latent space, the batch size and the learning rate were optimized using Keras-Tuner13 to 32, 32 and 5e-5, respectively.
Testing. We tested our trained network on both b0 images and the 88 volumes of b=1000s/mm2 (b1000). We removed N slices (simulating the outliers) in an alternating order from a given 3D volume, and we predicted them using the autoencoder. We did so by feeding their two neighbouring slices to the network and performed a weighted average in the latent space to generate the latent representation of the predicted N slices. The resulting latent representation was then decoded to predict the N slices in the voxel space (Figure 1, Testing).
Evaluation. The same N slices were also predicted using three baseline interpolation methods: trilinear, tricubic and 5th order B-Spline in four configurations: N=1,2 (slice gap of 1.5, 3mm); b0 or b1000 averaged per subject over the 88 volumes. We then compared each method to the N ablated ground truth (GT) slices. In addition to comparing the raw signal, we also assessed differences for various diffusion tensor derived metrics14, including the fractional anisotropy (FA), mean diffusivity (MD), axial diffusivity (AD) and radial diffusivity (RD) in four brain regions (i.e., cortical grey matter, white matter, corpus callosum and brainstem as provided by the dHCP). All comparisons were based on the mean squared error (MSE).

Results

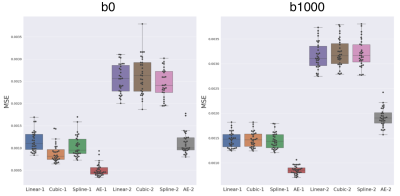
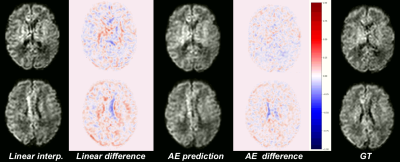
Our network trained solely on b0 images was able to generalize to b1000 contrast. Figure 2 shows the MSE between the GT and the four evaluated methods (linear, cubic, spline, and AE, see Methodology) for b0, b1000 and using N=1,2. We observe:
(1) The autoencoder outperforms the baselines methods in all configurations. An illustration of the error difference is shown in Figure 3.
(2) The gap between AE and other methods is larger for N=2 both for b0 and b1000.
(3) The error for b1000 is slightly higher than for b0, probably because of the higher contrast in the former.
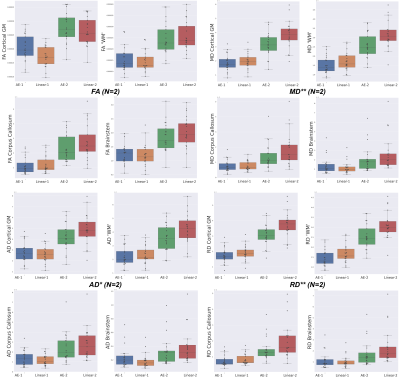
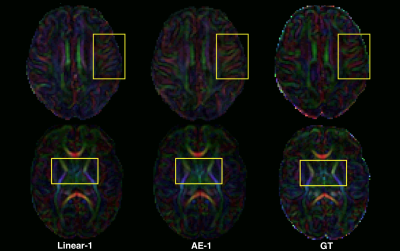
Regarding the scalar maps, we show AEs results (Figure 4) in comparison with the best performing baseline only (linear). We observed that AE for N=2 (and not N=1) outperforms the linear interpolation for all structures and maps (except FA in cortical grey matter). However, coloured FA maps for this configuration qualitatively show the increased consistency of the autoencoder with the GT in areas such as the internal capsules (Figure 5, bottom) or around the superficial white matter (Figure 5, top).

Conclusion

Autoencoders are valuable for overcoming motion-related artefacts in pre-term brain MRI and can improve white matter regions' conspicuity. By extracting prior knowledge from big datasets, deep learning has a clear advantage over interpolation methods. Notably, this work could be adapted via transfer learning to anisotropic fetal brain images to increase the through-plane resolution.

Acknowledgements

This work was supported by the Swiss National Science Foundation (project 205321-182602, grant No 185897: NCCR-SYNAPSY- "The synaptic bases of mental diseases" and the Ambizione grant PZ00P2_185814), the Centre d’Imagerie BioMédicale (CIBM) of the University of Lausanne (UNIL), the Swiss Federal Institute of Technology Lausanne (EPFL), the University of Geneva (UniGe), the Centre Hospitalier Universitaire Vaudois (CHUV), the Hôpitaux Universitaires de Genève (HUG), and the Leenaards and Jeantet Foundations.

References

1. Rodrigues, K. and Grant, P.E., 2011. Diffusion-weighted imaging in neonates. Neuroimaging Clinics, 21(1), pp.127-151.

2. Dubois, J., Alison, M., Counsell, S.J., Hertz‐Pannier, L., Hüppi, P.S. and Benders, M.J., 2021. MRI of the neonatal brain: a review of methodological challenges and neuroscientific advances. Journal of Magnetic Resonance Imaging, 53(5), pp.1318-1343.

3. Dyrby, T.B., Lundell, H., Burke, M.W., Reislev, N.L., Paulson, O.B., Ptito, M. and Siebner, H.R., 2014. Interpolation of diffusion weighted imaging datasets. Neuroimage, 103, pp.202-213.

4. Alexander, D.C., Zikic, D., Zhang, J., Zhang, H. and Criminisi, A., 2014, September. Image quality transfer via random forest regression: applications in diffusion MRI. In International Conference on Medical Image Computing and Computer-Assisted Intervention (pp. 225-232). Springer, Cham.

5. Chatterjee, S., Sciarra, A., Dünnwald, M., Mushunuri, R.V., Podishetti, R., Rao, R.N., Gopinath, G.D., Oeltze-Jafra, S., Speck, O. and Nürnberger, A., 2021. ShuffleUNet: Super resolution of diffusion-weighted MRIs using deep learning. arXiv preprint arXiv:2102.12898.

6. Elsaid, N.M. and Wu, Y.C., 2019, July. Super-resolution diffusion tensor imaging using SRCNN: A feasibility study. In 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) (pp. 2830-2834). IEEE.

7. Blumberg, S.B., Tanno, R., Kokkinos, I. and Alexander, D.C., 2018, September. Deeper image quality transfer: Training low-memory neural networks for 3d images. In International Conference on Medical Image Computing and Computer-Assisted Intervention (pp. 118-125). Springer, Cham.

8. Niethammer, M., Bouix, S., Aja-Fernández, S., Westin, C.F. and Shenton, M.E., 2007, October. Outlier rejection for diffusion weighted imaging. In International Conference on Medical Image Computing and Computer-Assisted Intervention (pp. 161-168). Springer, Berlin, Heidelberg.

9. Chang, L.C., Jones, D.K. and Pierpaoli, C., 2005. RESTORE: robust estimation of tensors by outlier rejection. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 53(5), pp.1088-1095.

10. Andersson, J.L., Graham, M.S., Zsoldos, E. and Sotiropoulos, S.N., 2016. Incorporating outlier detection and replacement into a non-parametric framework for movement and distortion correction of diffusion MR images. Neuroimage, 141, pp.556-572.

11. Sander, J., de Vos, B.D. and Išgum, I., 2021, February. Unsupervised super-resolution: creating high-resolution medical images from low-resolution anisotropic examples. In Medical Imaging 2021: Image Processing (Vol. 11596, p. 115960E). International Society for Optics and Photonics.

12. Garyfallidis, E., Brett, M., Amirbekian, B., Rokem, A., Van Der Walt, S., Descoteaux, M. and Nimmo-Smith, I., 2014. Dipy, a library for the analysis of diffusion MRI data. Frontiers in neuroinformatics, 8, p.8.

Figures

Figure 1. Network architecture (top): Each box is a multi-channel feature maps. The number of channels is denoted on top of each box. The violet box represents the latent space of the autoencoder. BN: Batch Normalization. ELU: Exponential Linear Unit. An illustration of how we generated middle slice(s) is shown in the testing, for the case of w=0.5 and b1000.

Figure 2. Mean squared error (MSE) between three baseline methods (linear, cubic and B-spline 5th order) and AE enhancement both for b0 (left) and b1000 (right). Two configurations were tried: N=1, i.e. either removing one slice and interpolate/synthesize it (Linear-1, Cubic-1, Spline-1, AE-1) or N=2, i.e. two slices (Linear-2, Cubic-2, Spline-2, AE-2). AE has a significantly lower MSE when compared to each respective best baseline method (paired Wilcoxon signed-rank test p <1.24e-09).

Figure 3. Illustration of the error difference in b1000 between the ground truth (GT) and the best baseline method (linear), and autoencoder (AE) enhancement.

Figure 4. Mean squared error (MSE) with respect to the GT of the best baseline method (Linear) and the autoencoder enhancement (AE) of the different structures (cortical grey matter (GM), white matter (WM), corpus callosum and brainstem) in each diffusion tensor map (FA, MD, AD and RD) for one slice removal (N=1) and two slices removal (N=2). Comparing the diffusion tensor maps of the merged brain region labels, we found that the autoencoder for N=2 outperforms other conventional methods for MD, RD and AD (paired Wilcoxon signed-rank test: ** p<0.0073 - * p<0.051).

Figure 5. Qualitative comparison of coloured FA in the one slice removed configuration (N=1) for the best baseline interpolation method, i.e. Linear-1 (left), autoencoder enhancement AE-1 (middle) and GT (right). The high frequency details (top) can be better captured by AE-1 as well as the internal capsules (bottom) that superimpose with the GT in contrast to a small deviation for Linear-1.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)
0300
DOI: https://doi.org/10.58530/2022/0300