0253

Ex vivo gray matter is complex: exchange & disorder exponents

Ileana O Jelescu^1,2 and Quentin Uhl¹
¹Radiology, Lausanne University Hospital (CHUV), Lausanne, Switzerland, ²CIBM Center for Biomedical Imaging, Ecole Polytechnique Federale de Lausanne, Lausanne, Switzerland

Synopsis

Fixation alters tissue properties significantly and in vivo vs ex vivo models should be adapted accordingly. Unlike in vivo studies of rodent gray matter (GM) where diffusion time-dependence D(t) was absent for t > 10 ms, allowing an interpretation of time-dependent kurtosis K(t) as resulting from inter-compartment exchange, here we show that ex vivo rodent GM displays marked D(t), with non-Gaussianity arising most probably from extracellular water. K(t) could thus result from combined effect of disorder and exchange. High-b data where extracellular water is preferentially suppressed may still enable the unconfounded estimation of exchange.

Introduction

Biophysical modeling of diffusion in gray matter (GM) is very promising, thanks to recent efforts to account for soma¹ and for potential structural disorder and inter-compartment exchange^2–4. In vivo rodent studies corroborate to report no diffusion time-dependence in GM within the 10–50 ms range^4–6, whereby time-dependent kurtosis can be largely attributed to exchange. A framework for estimating characteristic exchange time in addition to other model parameters has been recently proposed as NEXI (Neurite EXchange Imaging)⁴ or SMEX (Standard Model with EXchange)³. Here, we examine the properties of the diffusion signal in rat GM ex vivo, to determine whether the assumption of an exchange-dominated regime also holds, and how NEXI model parameter estimates compare to in vivo values. Furthermore, we highlight the potential of time-dependent features to characterize neurodegeneration.

Methods

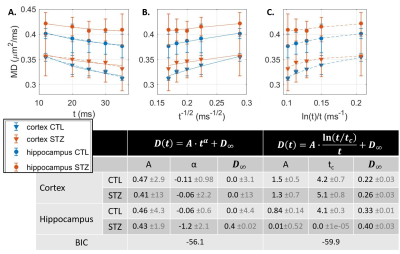
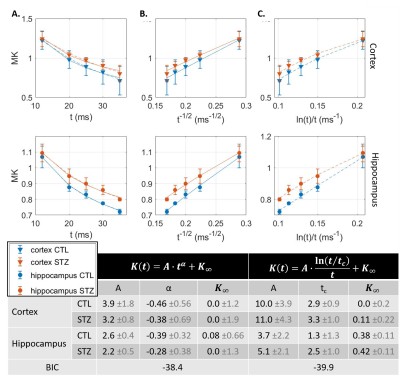
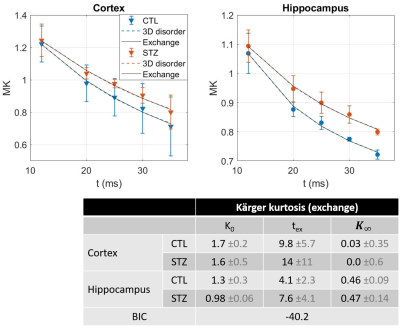
Experimental. All experiments were approved by the local Service for Veterinary Affairs. Five rat brains were extracted after transcardiac perfusion, further fixed in 4% PFA (48h) and rehydrated in PBS. Rats were either control (N=2) or Alzheimer’s (N=3), induced by intracerebroventricular injection of streptozotocin^7,8 (STZ). Samples were immersed in Fomblin and scanned at room temperature on a 14T system equipped with 1 T/m gradients, using a home-built volume saddle transceiver. Diffusion MRI data were acquired using a PGSE-EPI sequence, at b-values ranging 0–12 ms/μm² and diffusion times t ranging 12–35 ms (Fig. 1 provides acquisition parameters).
Processing. Images were denoised and corrected for Rician bias⁹ and spatial drift. Two ROIs corresponding to somatosensory cortex and dorsal hippocampus were drawn and signal was averaged across ROI voxels and samples for each group (CTL vs STZ). Mean diffusion $$$D(t)$$$ and kurtosis $$$K(t)$$$ were computed¹⁰ using b_max=5 ms/μm². $$$D(t)$$$ and $$$K(t)$$$ trends were analyzed against models of 1D or 3D structural disorder¹¹ as well as of two-compartment exchange^12,13:
$$$D(t)=A\cdot t^{\alpha}+D_{\infty};K(t)=B\cdot t^{\alpha}+K_{\infty}$$$, with α=-0.5 expected for 1D structural disorder (e.g. along neurites),
$$$D(t)=A\cdot \frac{\ln(t/t_{c})}{t}+D_{\infty};K(t)=B\cdot \frac{\ln(t/t_{c})}{t}+K_{\infty}$$$, for 3D structural disorder (e.g. in the extracellular space),
and $$$D(t)=D_{\infty};K(t)=K_{0}\cdot 2\frac{t_{ex}}{t}\left(1-\frac{t_{ex}}{t}\left(1-e^{-t/t_{ex}}\right)\right)+K_{\infty}$$$, for two-compartment exchange.
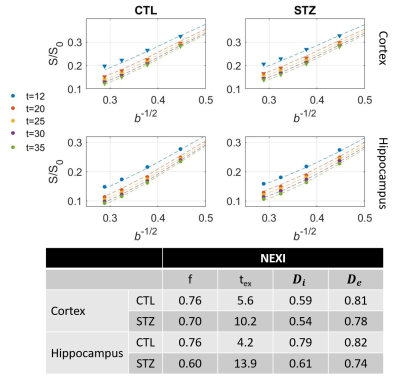
NEXI parameters (f, D_i, D_e, t_ex) were estimated by fitting the model to powder-averaged signals from all shells and diffusion times jointly.
Fitting was performed using non-linear least-squares. To control for local minima, fits were repeated N=100 times with random initialization and the solution with highest outcome frequency was retained (typically >80% trials).

Results & Discussion

Diffusion in ex vivo GM displayed time-dependence in the 12–35 ms range (Fig 2), decaying as t^-0.1, a lower exponent than expected from 1D disorder. The $$$D(t)$$$ decay was better fitted by the 3D disorder model with $$$t_{c}\sim4-5ms$$$, an estimate remarkably close to the diffusion pulse length δ=5ms. $$$K(t)$$$ decayed as t^-0.4, faster than $$$D(t)$$$. Setting aside the time-dependent diffusion (which is incompatible with exchange alone), $$$K(t)$$$ was explained almost equally well by 3D disorder ($$$t_{c}\sim1-3ms$$$) and exchange ($$$t_{ex}\sim4-14ms$$$), Figs. 3-4. Overall, these observations suggest ex vivo GM displays combined effects of non-Gaussian diffusion in the extracellular space – not found in vivo but possibly introduced by compartment shrinkage with fixation – and inter-compartment exchange.
With $$$D(t)$$$ possibly dominated by extracellular water and assuming most of extracellular signal is suppressed at high b-values, we used NEXI up to high b to estimate exchange. As for in vivo GM, signal dependence as 1/√b displayed a curvature distinct from the linear behavior of impermeable sticks, as well as increasing signal attenuation with diffusion time, both features consistent with exchange^3,4,14 (soma would also introduce a curvature but would display increasing signal with diffusion time) (Fig. 5). NEXI yielded estimates of neurite density $$$f=0.6-0.76$$$ and exchange times $$$t_{ex}\sim4-14ms$$$, in agreement with ex vivo literature³ and indeed shorter than in vivo estimates^4,15–17.
Time-dependent patterns differed between CTL and STZ groups. The STZ group displayed faster diffusivity and less marked time-dependence, compatible with a loss of tissue complexity at the micron-scale due to neurodegeneration⁷. Kurtosis was surprisingly also more elevated in the STZ group. One explanation could be a larger macroscopic heterogeneity in this group that would fuel kurtosis in the large ROI averaging. Remarkably, for both groups, K_∞ prediction was ~0 in cortex and ~0.4 in hippocampus, also consistent with heterogeneous hippocampus sub-fields and partial myelination. Finally, NEXI estimates for the STZ group showed reduced neurite density and longer exchange time t_ex that CTL. Given the small sample size, these group differences can however only be interpreted as trends.

Conclusion

While lower diffusivities and altered intra/extracellular fractions are well established features of tissue fixation, more subtle effects such as intra-compartment non-Gaussian diffusion could also vary between in vivo and ex vivo tissues and biophysical models should be adapted accordingly. In particular, while no diffusion time-dependence in rodent GM in vivo was reported for t > 10 ms, allowing an interpretation of $$$K(t)$$$ as resulting from inter-compartment exchange^4–6, here we show that ex vivo rodent GM displays marked $$$D(t)$$$ for t > 10 ms, with non-Gaussian diffusion arising most probably from extracellular water. $$$K(t)$$$ could thus reflect a combined effect of disorder and exchange. The availability of high-b data where extracellular water is preferentially suppressed may still enable the unconfounded estimation of t_ex but this approach requires further investigation. Longer diffusion times may also provide better discrimination of relevant mechanisms.

Acknowledgements

The authors thank Analina da Silva and Stefan Mitrea for assistance with animal surgery and perfusion, as well as Bernard Lanz and Claudia Zanella for providing the RF coil. This work was supported by the Swiss National Science Foundation under Eccellenza grant PCEFP2_194260 and by the CIBM Center for Biomedical Imaging, a Swiss research center founded and supported by Lausanne University Hospital (CHUV), the University of Lausanne (UNIL), the Swiss Federal Institute of Technology (EPFL), the University of Geneva (UNIGE) and Geneva University Hospital (HUG).

References

1. Palombo, M. et al. SANDI: A compartment-based model for non-invasive apparent soma and neurite imaging by diffusion MRI. NeuroImage 215, 116835 (2020).

2. Lee, H.-H., Papaioannou, A., Novikov, D. S. & Fieremans, E. In vivo observation and biophysical interpretation of time-dependent diffusion in human cortical gray matter. NeuroImage 222, 117054 (2020).

3. Olesen, J. L., Østergaard, L., Shemesh, N. & Jespersen, S. N. Diffusion time dependence, power-law scaling, and exchange in gray matter. arXiv:2108.09983 [physics] (2021).

4. Jelescu, I. O., de Skowronski, A., Palombo, M. & Novikov, D. S. Neurite Exchange Imaging (NEXI): A minimal model of diffusion in gray matter with inter-compartment water exchange. arXiv:2108.06121 [physics] (2021).

5. Pyatigorskaya, N., Le Bihan, D., Reynaud, O. & Ciobanu, L. Relationship between the diffusion time and the diffusion MRI signal observed at 17.2 Tesla in the healthy rat brain cortex. Magnetic resonance in medicine 72, 492–500 (2014).

6. Reynaud, O. et al. Surface-to-volume ratio mapping of tumor microstructure using oscillating gradient diffusion weighted imaging. Magnetic Resonance in Medicine 76, 237–247 (2016).

7. Tristão Pereira, C. et al. Synchronous nonmonotonic changes in functional connectivity and white matter integrity in a rat model of sporadic Alzheimer’s disease. NeuroImage 225, 117498 (2021).

8. Diao, Y., Yin, T., Gruetter, R. & Jelescu, I. O. PIRACY: An optimized pipeline for functional connectivity analysis in the rat brain. Front. Neurosci. 15, (2021).

9. Veraart, J. et al. Denoising of diffusion MRI using random matrix theory. NeuroImage 142, 394–406 (2016).

10. Veraart, J., Sijbers, J., Sunaert, S., Leemans, A. & Jeurissen, B. Weighted linear least squares estimation of diffusion MRI parameters: strengths, limitations, and pitfalls. NeuroImage 81, 335–46 (2013).

11. Novikov, D. S., Jensen, J. H., Helpern, J. A. & Fieremans, E. Revealing mesoscopic structural universality with diffusion. Proceedings of the National Academy of Sciences of the United States of America 111, 5088–93 (2014).

12. Kärger, J. NMR self-diffusion studies in heterogeneous systems. Advances in Colloid and Interface Science 23, 129–148 (1985).

13. Fieremans, E., Novikov, D. S., Jensen, J. H. & Helpern, J. A. Monte Carlo study of a two-compartment exchange model of diffusion. NMR in biomedicine 23, 711–24 (2010).

14. Veraart, J., Fieremans, E. & Novikov, D. S. On the scaling behavior of water diffusion in human brain white matter. NeuroImage 185, 379–387 (2019).

15. Bai, R., Springer, C. S., Plenz, D. & Basser, P. J. Fast, Na+/K+ pump driven, steady-state transcytolemmal water exchange in neuronal tissue: A study of rat brain cortical cultures. Magnetic Resonance in Medicine 79, 3207–3217 (2018).

16. Quirk, J. D. et al. Equilibrium water exchange between the intra- and extracellular spaces of mammalian brain. Magnetic Resonance in Medicine 50, 493–499 (2003).

17. Nilsson, M. et al. Noninvasive mapping of water diffusional exchange in the human brain using filter-exchange imaging. Magnetic resonance in medicine 69, 1573–81 (2013).

Figures

Fig 1. Diffusion MRI acquisition parameters and example cortical (red) and hippocampal (blue) ROI masks. All b-values were acquired for each diffusion time Δ (N=122 measurements per diffusion time, and N=610 measurements total). DKI fits used only shells up to b=5.

Fig 2. Time-dependence of mean diffusivity (MD) in each ROI and each group. Fit to a general power-law (solid lines in A and B) produced an exponent estimate α≈-0.1, lower than expected for 1D disorder (-0.5), albeit with large uncertainty. Fit to the 3D structural disorder functional form (dashed lines in A and C) produced a correlation time estimate t_c≈4-5 ms, close to the gradient pulse duration (δ=5ms) which suggests the finite pulse approximation could have been used. Bayesian Information Criterion (BIC) suggests 3D structural disorder explains D(t) in our data best.

Fig 3. Time-dependence of mean kurtosis (MK) in each ROI and each group. Fit of a general power-law to K(t) (solid lines in A and B) produced an exponent estimate α≈-0.4, more pronounced than for D(t) (Fig.2). Fit of the 3D structural disorder functional form (dashed lines in A and C) produced correlation time estimates t_c≈1.3-3.3 ms. BIC suggests 3D structural disorder explains K(t) in our data better than the general power-law but less well than exchange (Fig.4). The more pronounced time exponent of K(t) vs D(t) points to added contributions from 3D disorder and exchange.

Fig 4. Time-dependence of mean kurtosis (MK) in each ROI and each group. Fit of the Kärger kurtosis from two-compartment exchange (black solid lines) produced exchange time estimates t_ex≈4-14 ms and highly similar fit quality to 3D disorder (colored dashed lines). BIC though suggests exchange to be the best fitting model to our data (vs Fig.3).

Fig 5. Powder-averaged signals in each ROI and group, for different diffusion times, over 1/√b. The distinct curvature confirms the tissue cannot be modeled as impermeable sticks, and lower signal with increasing diffusion time is a signature of exchange rather than of soma compartment (though the latter may contribute as well). NEXI model estimation yields neurite fractions perfectly in line with histology and exchange times similar to those from K(t) and to other recent ex vivo studies.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

0253

DOI: https://doi.org/10.58530/2022/0253