0252
Isolating restriction and exchange in gray matter using double and single diffusion encodings with equal diffusion weighting1Department of Clinical Neurosciences, Wellcome Centre for Integrative Neuroimaging, FMRIB, University of Oxford, Oxford, UK, United Kingdom, 2Section on Quantitative Imaging and Tissue Sciences, Eunice Kennedy Shriver National Institute of Child Health and Human Development, Bethesda, MD, United States, 3National Institute of General Medical Sciences, Bethesda, MD, United States, 4Celoptics, Inc., Rockville, MD, United States
Synopsis
The diffusion MR signal in complex tissue such as gray matter exhibits non-Gaussian signal attenuation due to exchange and restrictions. Existing signal models typically ignore one or both effects by assuming Gaussian diffusion or negligible exchange. We propose a more rigorous signal model that incorporates both effects. Subsequently, an acquisition scheme utilizing equal double diffusion encodings ($$$b_1=b_2$$$) at various mixing times, and single diffusion encodings with the same total weighting $$$b=b_1+b_2$$$, is designed to independently characterize the effects of restriction and exchange. The method is tested on live and fixed gray matter specimen using a low-field, high-gradient MR system.
Introduction
Diffusion microstructural MR aims to probe tissue microstructure and extract parameters via signal models. For white matter, the field has conjectured a “standard model”1,2 consisting of water confined in myelinated axons and neurites, modelled as impermeable cylinders, and extra-cellular water presumed to undergo hindered, Gaussian diffusion – ignoring exchange. While this standard model and extensions thereof3 have been effective for understanding some features of white matter, they have failed to translate to gray matter,1,4,5 perhaps due to higher expected membrane permeabilities of gray matter components,6,7 e.g., astrocytes highly expressing aquaporin.8 In contrast, models of exchange such as the Kärger model9 typically exclude restriction and assume that signal components have different but otherwise Gaussian diffusivities.10,11 This assumption may underestimate exchange rates, as slower signal attenuation at high $$$b$$$-values is attributed to slower exchange, rather than non-Gaussian signal attenuation.To advance the study of complex tissue using diffusion MR, we propose a rigorous signal model for certain experimental parameters that incorporates both restriction and exchange. With this model in mind, we design an acquisition scheme to characterize restriction and exchange independently. The method utilizes single and double diffusion encodings (S/DDEs) with equal total $$$b$$$-values to remove Gaussian diffusion. Diffusion exchange spectroscopy (DEXSY) measurements,12 (i.e., DDEs with a storage time $$$t_m$$$) at a fixed $$$b$$$-value but varied $$$t_m$$$ are then used to separate restriction and exchange. The method is tested on ex vivo neonatal mouse spinal cord (consisting mostly of gray matter13) using a permanent magnet system with a strong static gradient (SG).
Theory
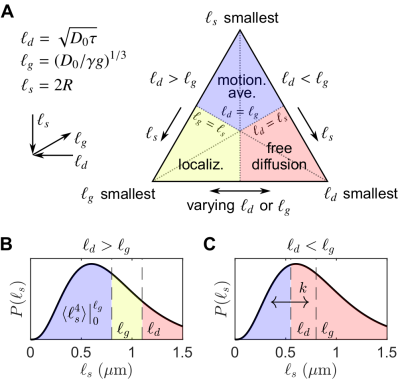
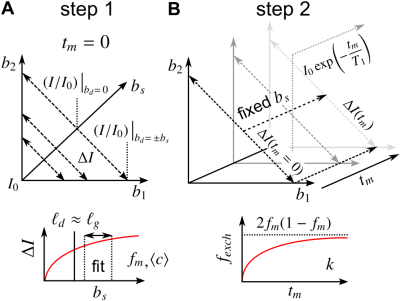
Consider spin echoes formed under an SG with constant amplitude $$$g$$$ and variable echo time $$$2\tau$$$. The regimes of signal behavior14,15 are associated with three length scales: (i) the diffusion length $$$\ell_d = \sqrt{D_0\tau}$$$; (ii) the gradient dephasing length, $$$\ell_g=(D_0/\gamma^{}g)^{1/3}$$$; and (iii) the structural length, or size of restriction in the gradient direction, $$$\ell_s$$$. The free diffusion regime corresponds to $$$\ell_d$$$ being the shortest of $$$\ell_d,\ell_g,\ell_s$$$; diffusion is Gaussian, and the normalized echo intensity is $$$I/I_0=\exp{\left(-bD_0\right)}$$$, where $$$b=(2/3)\gamma^2g^2\tau^3$$$. The motional averaging regime corresponds to $$$\ell_s$$$ being shortest. The localization regime – in which there may be persistent signal localized near boundaries – corresponds to $$$\ell_g$$$ being shortest. The signal attenuation in both non-Gaussian regimes is characterized by $$$I/I_0\propto\exp{\left(-b^{1/3}\right)}$$$ in the limit of large $$$\ell_d$$$.16For heterogeneous tissue, $$$\ell_s$$$ values may be distributed with a probability density function (PDF) $$$P(\ell_s)$$$ (see Fig. 1).17 When $$$\ell_d\gtrsim\ell_g$$$, the signal may be approximated as two signal fractions demarcated by $$$\ell_g$$$, $$$f_e$$$ ($$$\ell_s>\ell_g$$$), and $$$f_m$$$ ($$$\ell_s\lesssim\ell_g$$$), corresponding to freely diffusing and motionally-averaged signal attenuating with18 $$I/I_0\simeq\exp{\left(-b^{1/3}\langle^{}c\rangle\right)},\;\;\ell_d\gg2\langle^{}R\rangle\\\langle^{}c\rangle=\frac{4}{175}\frac{\gamma^{4/3}g^{4/3}\langle^{}R^4\rangle}{(2/3)^{1/3}D_0},\tag{1}$$ respectively, where $$$R=\ell_s/2$$$ is an effective spherical radius and $$$\langle\rangle$$$ denotes ensemble-averaging over $$$R=\left[0,\ell_g/2\right]$$$. Given that $$$\ell_d\gtrsim\ell_g$$$ and ignoring exchange during encodings and relaxation processes, $$$I/I_0$$$ for a DEXSY experiment becomes $$\frac{I}{I_0}=f_{m,m}\exp{\left(-\left[b_1^{1/3}+b_2^{1/3}\right]\langle^{}c\rangle\right)}+f_{m,e}\exp{\left(-b_1^{1/3}\langle^{}c\rangle-b_2D_0\right)}\\+f_{e,m}\exp{\left(-b_1D_0-b_2^{1/3}\langle^{}c\rangle\right)}+f_{e,e}\exp{\left(-[b_1+b_2]D_0\right)},\tag{3}$$ where $$$f_m=f_{m,e}+f_{m,m}$$$ and $$$f_m,f_e$$$ are exchanging fractions dependent on $$$t_m$$$. Applying the similarity transform to the sum $$$b_s=b_1+b_2$$$ and difference $$$b_d=b_1-b_2$$$ in $$$b$$$-values described in Refs.19,20,21 and taking a finite difference approximation of the curvature in $$$I/I_0$$$ w.r.t. $$$b_d$$$ about $$$b_d=0$$$ (fixing $$$b_s$$$), we remove the non-exchanging Gaussian diffusion contribution, and the exchanging fraction $$$f_{exch}=f_{m,e}+f_{e,m}=2f_{m,e}$$$ (by mass balance) can be written as $$f_{exch}(t_m)=\frac{2\left[\Delta^{}I(t_m)-\Delta^{}I(t_m=0)-f_ma_1b_s^2\right]}{b_s^2\left[a_0\exp{\left(-2^{-1/3}b_s^{1/3}\langle^{}c\rangle-2^{-1}b_sD_0\right)}-a_1\right]},\;\;t_m>0\\=2f_m(1-f_m)\left[1-\exp{\left(-t_mk\right)}\right],\tag{3}$$ where $$\Delta^{}I(t_m)=(I/I_0)\bigr|_{b_d=\pm^{}b_s}-(I/I_0)\bigr|_{b_d=0}\tag{4}$$ is the difference between equal DDEs ($$$b_d=0,b_1=b_2$$$) and SDEs with the same $$$b=b_s$$$, $$a_0=\left(\frac{\langle^{}c\rangle}{3\left[2^{1/3}b_s^{2/3}\right]}-\frac{D_0}{2}\right)^2+\frac{2^{2/3}\langle^{}c\rangle}{9b_s^{5/3}},\;\;a_1=\frac{\langle^{}c\rangle}{18}\left(\frac{2}{b_s}\right)^{5/3}\exp{\left(-2\left[\frac{b_s}{2}\right]^{1/3}\langle^{}c\rangle\right)},\tag{5}$$ and $$$k$$$ is a first-order exchange rate.9 Restriction and exchange can be further separated by varying $$$t_m$$$. At small $$$t_m$$$ (i.e., $$$t_m\ll^{}1/k$$$), $$$f_{exch}\approx^{}0$$$, such that $$$\Delta^{}I$$$ depends only on $$$f_m,\langle^{}c\rangle$$$, $$\Delta^{}I(b_s,t_m=0)=f_m\left[\exp{\left(-b_s^{1/3}\langle^{}c\rangle\right)}-\exp{\left(-2^{2/3}b_s^{1/3}\langle^{}c\rangle\right)}\right].\tag{6}$$ Eq. (6) can thus be fit for $$$f_m,\langle^{}c\rangle$$$, after which Eq. (3) can be fit for $$$k$$$ (see Fig. 2).
Methods
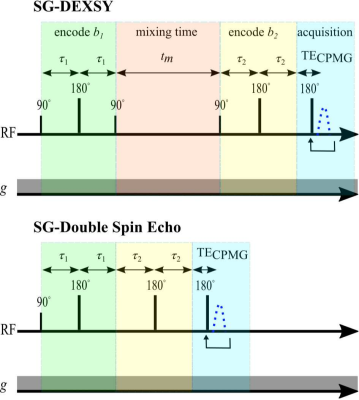
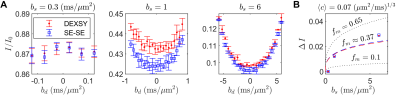
DEXSY (SG-DEXSY) and double spin echo (SG-SE-SE) pulse sequences (Fig. 3) were implemented on a PM-10 NMR MOUSE single-sided magnet ($$$\omega_0=13.79\;\mathrm{MHz}$$$, $$$B_0=0.3239\;\mathrm{T}$$$, $$$g=15.3\;\mathrm{T/m}$$$) with a home-built solenoid RF coil and test chamber. RF pulse lengths $$$=2/2\;\mathrm{\mu^{}s}$$$, pulse powers $$$=-22/-16\;\mathrm{dB}$$$, $$$\mathrm{TR}=2\;\mathrm{s}$$$, 2000 or 8000 echo CPMG train with $$$\mathrm{TE}=25\;\mathrm{\mu^{}s}$$$, 8 points per echo, and $$$0.5\;\mathrm{\mu^{}s}$$$ dwell time. Normalization $$$I_0$$$ corresponds to $$$b=0.089\;\mathrm{ms/\mu^{}m^2}$$$. Viable and fixed ex vivo neonatal (postnatal day 1–4) mouse spinal cords were studied. Spinal cords were bathed in artificial cerebrospinal fluid at 95% O2/5% CO2 and 25$$${}^\circ$$$C. More experimental details can be found in Refs.20,21 Curvature along $$$b_d$$$ was assessed at $$$b_s=[0.3,1,6]\;\mathrm{ms/\mu^{}m^2}$$$ on a viable spinal cord using both sequences. In addition, $$$\Delta^{}I$$$ was assessed at $$$b_s=[2,3,3.5,4,4.5,5,6,8,10,13,20,30,60,100]\;\mathrm{ms/\mu^{}m^2}$$$ and $$$t_m=[0.2,2,10,20,160] \;\mathrm{ms}$$$ on a fixed spinal cord using the SG-DEXSY sequence.20Results
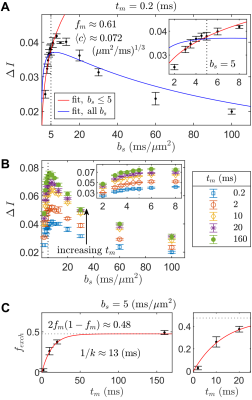
Increasing curvature depth with $$$b_s$$$ is observed in viable spinal cord (Fig. 4). Exemplar plots of Eq. (6) are shown (Fig. 4B). SG-DEXSY data ($$$t_m=0.2\;\mathrm{ms}$$$) acquired on fixed spinal cord was fit to Eq. (6) using all $$$b_s$$$ values or $$$b_s=[2,3,3.5,4,4.5,5]\;\mathrm{ms/\mu^{}m^2}$$$, corresponding to $$$1.37\,\ell_g<\ell_d<1.6\,\ell_g$$$ (Fig. 5A). The truncated fit (i.e., whilst $$$\ell_d\gtrsim\ell_g$$$) is better and yields $$$f_m\approx0.61,\,\langle^{}c\rangle\approx0.072\;(\mathrm{\mu^{}m^{2}/ms})^{1/3}$$$. Fixing $$$b_s=5\;\mathrm{ms/\mu^{}m^2}$$$, calculated $$$f_{exch} (t_m)$$$ values were fit to Eq. (3), yielding $$$k=75\;\mathrm{s^{-1}}$$$ (Figs. 5B–C).Conclusion
Good fits are obtained to experimental data whilst $$$\ell_d\gtrsim\ell_g$$$, demonstrating the feasibility of the signal model and experimental approach. Apparent tissue parameters $$$f_m,\langle^{}c\rangle$$$ characterizing restrictions similar to and smaller than $$$\ell_g=(D_0/\gamma^{}g)^{1/3}$$$ and an exchange rate are measured. Approaches leveraging well-designed multidimensional ($$$b_1,b_2,t_m$$$) diffusion MR experiments may thus enable the isolation of restriction and exchange, though challenges remain in adapting such methods to high-field scanners.Acknowledgements
TXC, RR, and PJB were all supported by the IRP of the NICHD, NIH. TXC is a graduate student in the NIH-Oxford Cambridge Scholars program. NHW was funded by the NIGMS PRAT Fellowship Award #FI2GM133445-01.
We thank Dr. Alexandru Avram and Dr. Michal Komlosh for helpful discussions about double diffusion encoding and Dr. Denis Grebenkov for discussions about the implications of non-Gaussian signal attenuation in DEXSY experiments.
References
1. Novikov DS, Fieremans E, Jespersen SN, Kiselev VG. Quantifying brain microstructure with diffusion mri: Theory and parameter estimation. NMR in Biomedicine. 2019;32:e3998.
2. Veraart J, Fieremans E, Novikov DS. On the scaling behavior of water diffusion in human brain white matter. NeuroImage. 2019;185:379–387.
3. Palombo M, Ianus A, Guerreri M, Nunes D, Alexander DC, Shemesh N, et al. Sandi: A compartment-based model for non-invasive apparent soma and neurite imaging by diffusion mri. NeuroImage. 2020;215:116835.
4. Novikov DS, Jensen JH, Helpern JA, Fieremans E. Revealing mesoscopic structural universality with diffusion. Proceedings of the National Academy of Sciences of the United States of America. 2014;111:5088–5093.
5. Jelescu IO, Palombo M, Bagnato F, Schilling KG. Challenges for biophysical modeling of microstructure. Journal of Neuroscience Methods. 2020:108861.
6. Yang DM, Huettner JE, Bretthorst GL, Neil JJ, Garbow JR, Ackerman JJ. Intracellular water preexchange lifetime in neurons and astrocytes. Magnetic Resonance in Medicine 2018;79: 1616–1627.
7. Veraart J, Fieremans E, Rudrapatna U, Jones D, Novikov DS. Biophysical modeling of the gray matter: does the “stick” model hold. Proceedings of the 27th Annual Meeting of ISMRM; 2018.
8. Papadopoulos MC, Verkman AS. Aquaporin water channels in the nervous system. Nature Reviews Neuroscience. 2013;14:265–277.
9. Kärger J. Nmr self-diffusion studies in heterogeneous systems. Advances in Colloid and Interface Science. 1985;23:129–148.
10. Nilsson M, Alerstam E, Wirestam R, Sta F, Brockstedt S, L ̈att J, et al. Evaluating the accuracy and precision of a two-compartment kärger model using monte carlo simulations. Journal of Magnetic Resonance. 2010;206:59–67.
11. Moutal N, Nilsson M, Topgaard D, Grebenkov D. The kärger vs bi-exponential model: Theoretical insights and experimental validations. Journal of Magnetic Resonance. 2018;296:72–78.
12. Callaghan P, Furó I. Diffusion-diffusion correlation and exchange as a signature for local order and dynamics. The Journal of Chemical Physics. 2004;120:4032–4038.
13. Sengul G, Puchalski RB, Watson C. Cytoarchitecture of the spinal cord of the postnatal (p4) mouse. The Anatomical Record: Advances in Integrative Anatomy and Evolutionary Biology. 2012;295:837–845.
14. Hürlimann MD, Helmer K, de Swiet T, Sen P. Spin echoes in a constant gradient and in the presence of simple restriction. Journal of Magnetic Resonance. 1995;113:260–264.
15. Axelrod S, Sen PN. Nuclear magnetic resonance spin echoes for restricted diffusion in an inhomogeneous field: Methods and asymptotic regimes. The Journal of Chemical Physics. 2001;114:6878–6895.
16. Grebenkov DS. Diffusion mri/nmr at high gradients: Challenges and perspectives. Microporous and Mesoporous Materials. 2018;269:79–82.
17. Moutal N, Grebenkov DS. The localization regime in a nutshell. Journal of Magnetic Resonance. 2020;320:106836.
18. Neuman C. Spin echo of spins diffusing in a bounded medium. The Journal of Chemical Physics. 1974;60:4508–4511.
19. Cai TX, Benjamini D, Komlosh ME, Basser PJ, Williamson NH. Rapid detection of the presence of diffusion exchange. Journal of Magnetic Resonance. 2018;297:17–22.
20. Williamson NH, Ravin R, Benjamini D, Merkle H, Falgairolle M, O’Donovan MJ, Blivis D, Cai TX, Ghorashi NS, Bai R, Basser PJ. Magnetic resonance measurements of cellular and sub-cellular membrane structures in live and fixed neural tissue. eLife. 2019;8:e51101.
21. Williamson NH, Ravin R, Cai TX, Benjamini D, Falgairolle M, O’Donovan MJ, Basser PJ. Real-time measurement of diffusion exchange rate in biological tissue. Journal of Magnetic Resonance. 2020;317:106782.
Figures