0250
What Does FEXI Measure?1A.I.Virtanen Institute for Molecular Sciences, University of Eastern Finland, Kuopio, Finland, 2Department of Radiology, University Medical Center Freiburg, Freiburg, Germany
Synopsis
Filter-EXchange Imaging (FEXI) evaluates the permeability of cell membranes, which is already used in clinical research. It relies on suppressing the extracellular signal using strong diffusion weighting (mobility filter causing a reduction in the overall diffusivity) and monitoring the subsequent diffusivity recovery. Using simulations, we demonstrate the presence of a spurious exchange: In compartments with complex geometry, there are locations where spins remain unaffected by the mobility filter. Moving to other locations afterward contributes to the diffusivity recovery, thus mimicking exchange. The discovered phenomenon opens large room for investigation towards characterizing the compartment geometry and crystallizing the genuine membrane permeation.
INTRODUCTION
Inspired by the diffusion exchange spectroscopy technique 1,2, the double PGSE sequence with stimulated echo was modified to have gradients pairs of different magnitude. This gave rise to the filter exchange imaging (FEXI)3 for measuring the apparent exchange rate (AXR) between compartments with different diffusivities (Fig.1). The first gradient pair acts as the diffusion (or mobility) filter suppressing the compartment with high diffusivity. The second gradient pair measures the diffusion coefficient for different mixing times, revealing the recovery to the unperturbed value. FEXI is commonly considered as a way to access the cell membrane permeability for water. The method was validated in yeast suspension and numerical simulations 4. Being implemented on clinical MRI scanners 4, it has been applied to study human brain tissue 5, 6, brain tumors 7, breast cancer 8, and human embryonic kidney 9.In this work, we show that FEXI is not uniquely sensitive to the transcytolemmal exchange, but also to the geometry of involved compartments. In a complex geometry, water in some "pockets" such as suitably oriented channels can avoid suppression by the mobility filter and then move during the mixing time to channels with different orientations where it contributes to a high diffusivity (Fig. 2). This can occur without crossing any membrane. For the first illustration of this mechanism, we use Monte Carlo simulations in large compartments of complex geometry with impermeable boundaries (Fig. 3). While these substrates do not include any permeable membranes, our simulation results show a spurious AXR that can lead to misinterpretation of data.
METHODS
Synthetic MediaWe generated a set of three-dimensional media with different geometrical complexity. All media are described by the indicator function $$$v(r)$$$ taking the values 0 and 1 in intra- and extra-cellular compartments. These media are periodic in all three directions, initially created in the continuous space, then mapped in the lattice with the size 2563. The media in the complex-geometry group, which we refer to as "spaghetti", were generated using the algorithm developed for simulating the capillary network 10. We generated two "spaghetti" media, one strongly anisotropic with the volume fraction $$$\zeta=$$$ 0.51and one isotropic with $$$\zeta=$$$0.49, shown in Fig 3. (a-b). The medium in the simple-geometry group consisted of identical spheres with the value $$$v(r)=$$$1 inside. This medium was generated using a collision-driven algorithm 11, 12. Utilizing this algorithm, we generated one medium with the volume fraction of spheres 57% (Fig 3. (c)).
Monte Carlo Simulation
We used a C++ program, which was previously developed for simulating transverse relaxation, diffusion, and the Larmor frequency shift 10, 13-15. The algorithm is based on the nearest-neighbor hopping on a cubic lattice. The diffusion-weighting gradients were simulated in the narrow-pulse limit as a phase instantly acquired according to the spin's current displacement from its initial position. The gradients and the instant rotations simulating the radiofrequency pulses were applied according to the scheme shown in Fig. 1. To focus on the diffusion effect, we did not assign any transverse relaxation or magnetic susceptibility associated with $$$v(r)=$$$1. The simulation outcome was the genuine cumulative diffusion tensor and the simulated MR signal for multiple combinations of the FEXI parameters. The diffusion tensor was calculated via the spin's displacements, $$D_{ab} = \frac{1}{2t} \langle {r_a r_b} \rangle $$ where $$$a,b=$$$1,2,3 label the spatial directions, $$$t$$$ is the diffusion time, and the averaging is performed over all spins.
RESULTS: SPURIOUS EXCHANGE
The FEXI results for considered media are shown in Fig. 4 for diffusion inside tubes or spheres. The most pronounced spurious exchange is present for the most complex geometries (anisotropic spaghetti across the principal diffusion direction and the isotropic one). The magnitude of the effect and the spurious exchange time decrease for simpler geometries (the principal direction in the anisotropic spaghetti and in packed spheres). Measurement in the direction orthogonal to the filter direction could result in enhanced ADC right after the filter, according to the logic illustrated in Fig. 2. This effect is, however, not visible for the considered media (Fig 4. (f)).DISCUSSION and CONCLUSION
We have demonstrated that FEXI-derived ADC is not purely a function of transcytolemmal exchange but is also contributed by the geometrical complexity of compartments explored by diffusing MR-reporting molecules. Depending on the compartment geometry, spins may find "shelters" with low mobility to survive the filter gradient (Fig. 2). Such spins lead to a reduction in the ADC right after the filter with a following recovery, thus mimicking the FEXI-revealed exchange. Clean separation of this phenomenon from the true exchange is currently unavailable, mainly due to the absence of quantitative theory. The separation might be easier for significantly different time scales of these effects. Exploring the large parameter space of FEXI might help, in particular studying multiple mutual orientations of the filter and detection gradients. Further work will focus on these unresolved problems and more realistic media.Acknowledgements
This work was supported by the Academy of Finland (grant #323385 to A.S.) and the Erkko Foundation (A.S.)References
1. PT Callaghan and Istvan Furo. Diffusion-diffusion correlation and exchange as a signature for local order and dynamics. The Journal of chemical physics, 120(8):4032–4038, 2004. 2. Marcel Gratz, Markus Wehring, Petrik Galvosas, and Frank Stallmach. Multi-dimensional NMR diffusion studies in microporous materials. Microporous and mesoporous materials, 125(1-2):30–34, 2009.
3. Ingrid Aslund, Agnieszka Nowacka, Markus Nilsson, and Daniel Topgaard. Filter-exchange PGSE NMR determination of cell membrane permeability. Journal of Magnetic Resonance, 200(2):291–295, 2009.
4. Samo Lasič, Markus Nilsson, Jimmy Lätt, Freddy Ståhlberg, and Daniel Topgaard. Apparent exchange rate mapping with diffusion MRI. Magnetic resonance in medicine, 66(2):356–365, 2011
5. Markus Nilsson, Jimmy Lätt, Danielle van Westen, Sara Brockstedt, Samo Lasič, Freddy Ståhlberg, and Daniel Topgaard. Noninvasive mapping of water diffusional exchange in the human brain using filter-exchange imaging. Magnetic resonance in medicine, 69(6):1572–1580, 2013.
6. Ruiliang Bai, Zhaoqing Li, Chaoliang Sun, Yi-Cheng Hsu, Hui Liang, and Peter Basser. Feasibility of filter-exchange imaging (FEXI) in measuring different exchange processes in human brain. Neuroimage, 219:117039,2020.
7. Björn Lampinen, Filip Szczepankiewicz, Danielle van Westen, Elisabet Englund, Pia C Sundgren, Jimmy, Lätt, Freddy Ståhlberg, and Markus Nilsson. Optimal experimental design for filter exchange imaging: Apparent exchange rate measurements in the healthy brain and in intracranial tumors. Magnetic resonance in medicine,77(3):1104–1114, 2017.
8. Samo Lasič, Stina Oredsson, Savannah C Partridge, Lao H Saal, Daniel Topgaard, Markus Nilsson, and Karin Bryskhe. Apparent exchange rate for breast cancer characterization. NMR in biomedicine, 29(5):631–9, May 2016.
9. Franz Schilling, Susana Ros, De-En Hu, Paula D’Santos, Sarah McGuire, Richard Mair, Alan J Wright, Elizabeth Mannion, Robin JM Franklin, André A Neves, et al. MRI measurements of reporter-mediated increases in transmembrane water exchange enable detection of a gene reporter. Nature biotechnology, 35(1):75–80, 2017.
10. Dmitry S. Novikov, Marco Reisert, and Valerij G. Kiselev. Effects of mesoscopic susceptibility and transverse relaxation on diffusion NMR. Journal of Magnetic Resonance, 293:134 – 144, 2018.
11. Monica Skoge, Aleksandar Donev, Frank H Stillinger, and Salvatore Torquato. Packing hyperspheres in high-dimensional Euclidean spaces. Physical Review E,74(4):041127, 2006.
12. https://torquato.princeton.edu/links-and-codes/sphere-packings-software-download/
13. Dmitry S. Novikov and Valerij G. Kiselev. Transverse NMR relaxation in magnetically heterogeneous media. Journal of Magnetic Resonance,195(1):33–39, November 2008.
14. Alexander Ruh, Harald Scherer, and Valerij G Kiselev. The Larmor frequency shift in magnetically heterogeneous media depends on their mesoscopic structure. Magnetic resonance in medicine, 79(2):1101–1110, Feb 2018.
15. Alexander Ruh and Valerij G. Kiselev. Larmor frequency dependence on structural anisotropy of magnetically heterogeneous media. Journal of Magnetic Resonance, 307:106584, 2019.
Figures
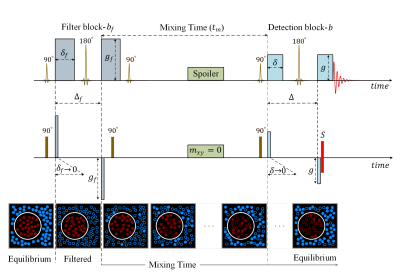
Schematic diagram of FEXI sequence and how it is simulated in this study. FEXI concatenates a filter block and a detection block separated by mixing time $$$t_m$$$. The bottom row shows the common interpretation of FEXI. Solid circles stand for molecules contributing to the signal, empty circles for the signal suppressed by the filter. Red and blue colors correspond to low and high diffusivity, respectively ("molecules" change color upon crossing the membrane).
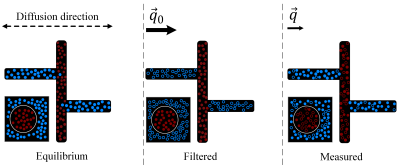
The proposed mechanism for spurious exchange, the squares with a round cell are shown for comparison with the common interpretation as in Fig.1. In a compartment with complex geometry, some water escapes suppression by the mobility filter in locations with low mobility in the direction of the filter gradient. The following diffusional motion mimics exchange while occurring within the same compartment with no permeation through any membrane.
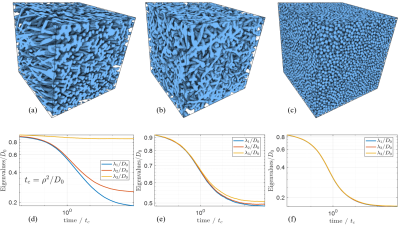
Synthetic media used in this study, all obeying periodic boundary conditions in three spatial directions. (a) Anisotropic "spaghetti" medium formed by a randomized, self-crossing tube. (b) Isotropic "spaghetti" medium. (c) A medium formed by random packing of identical spheres with density 57%. (d-f) The time-dependent eigenvalues of corresponding diffusion tensors for "intra-cellular" diffusion. The leveling-off for the spheres reflects percolation between touching spheres. $$$D_0$$$ is the bulk diffusion coefficient, and $$$\rho$$$ is the radius of spheres and tubes.
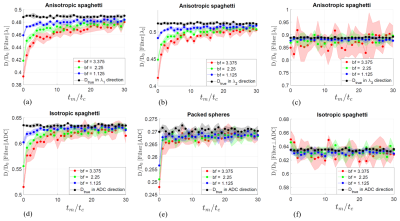
Simulation results for diffusion in intra-space of considered media, color bands at one standard deviation. Panels (a-e) show results for the coinciding directions of mobility filter and the measurement. The two directions are orthogonal in panel (f), $$$ \Delta = 1.5t_c $$$, $$$t_c$$$ was defined in Fig.3. A pronounced spurious exchange is seen for isotropic (d) and across the principal tube direction in anisotropic spaghetti (a,b).