0249

A multi-echo low-rank and sparse algorithm that reduces the bias of global fluctuations on the estimation of neuronal signal
Eneko Uruñuela1, Stefano Moia1, and César Caballero-Gaudes1
1Basque Center on Cognition, Brain and Language, Donostia - San Sebastián, Spain

Synopsis

This work introduces a novel multi-echo fMRI deconvolution approach that reduces the effect of global fluctuations (e.g., motion effects, physiological confounds, artefacts) on blindly mapping the brain’s response to single-trial BOLD events without prior timing information. The new sparse-plus-low-rank multi-echo multivariate paradigm free mapping (SPLORA) algorithm is compared with a trial-based known-timing GLM analysis and its predecessor multivariate multiecho paradigm free mapping (MvME-PFM) approach. This method allows exploring the brain’s functional dynamics during task, naturalistic and resting-state paradigms, being less affected by motion and physiological confounds, thus avoiding global signal regression to estimate neuronal related activity with multi-echo fMRI.

Introduction

Denoising the blood oxygen level-dependent (BOLD) signal is central for studying brain organization and dynamics with functional MRI (fMRI) data. Nevertheless, structured noise from head motion, cardiac-related brain pulsations, hardware artifacts, and respiratory variations can considerably corrupt fMRI signal dynamics, making the distinction of neurobiological signals difficult1,2. Multi-echo (ME) fMRI techniques are a promising resource to discern neuronal signals based on the signal decay properties and have been shown to be excellent at removing spatially focal artifacts (e.g. due to motion)1,3,4. However, widespread changes in the BOLD signal that occur due to large respiratory events are especially hard to isolate from neuronal signals even after ME-ICA denoising since their temporal signature often matches the hemodynamic response. Algorithms that aim to extract the underlying neuronal-related signal related to BOLD events face the same problem, and their performance is considerably diminished by these widespread artifacts. Here, we present a novel multi-echo sparse and low-rank (SPLORA) paradigm free mapping (PFM) algorithm that aims to disentangle the neuronal-related BOLD signal changes from global signal fluctuations.

Theory

Signal model: The concatenation of K multi-echo fMRI datasets $$$\mathbf{Y}_k$$$ for $$$k=1,\ldots,K$$$ time echoes ($$$\mathrm{TE}$$$) (in signal percentage change) can be decomposed as:
$$\left[\begin{array}{c}\mathbf{Y}_{1} \\ \vdots \\\mathbf{Y}_{K} \end{array}\right]=-\left[\begin{array}{c} \mathrm{TE}_{1} \mathbf{H} \\ \vdots \\\mathrm{TE}_{K} \mathbf{H} \end{array}\right] \mathbf{S} + \mathbf{L} + \mathbf{N},$$ or $$\mathbf{\overline{Y}} = \mathbf{\overline{H} S} + \mathbf{L} + \mathbf{N},$$
where $$$\mathbf{\overline{Y}} \in \mathbb{R}^{K N \times V}$$$, $$$\mathbf{L} \in \mathbb{R}^{K N \times V}$$$ denotes a matrix modelling global low-rank signals, $$$\mathbf{\overline{H}} \in \mathbb{R}^{E \cdot N \times N}$$$ is the discrete convolution matrix with the HRF, $$$\mathbf{S} \in \mathbb{R}^{N \times V}$$$ is the underlying activity-inducing signal (in terms of R2* changes)5, and $$$\mathbf{N} \in \mathbb{R}^{E \cdot N \times V}$$$ is assumed as random Gaussian noise.
Optimization problem: $$\hat{\mathbf{L}}, \hat{\mathbf{S}}=\arg \min _{\mathbf{L,S}} \frac{1}{2}\|\overline{\mathbf{Y}}- \overline{\mathbf{H}} \mathbf{S} - \mathbf{L}\|_{2}^{2} + \lambda_L \| \mathbf{L} \|_* + \lambda_S \Omega(\mathbf{S}),$$
where $$$\Omega(\mathbf{S})$$$ is a penalty that promotes sparsity on the estimates of the activity-inducing signal $$$\mathbf{S}$$$, the nuclear norm promotes low-rankness on the estimates of global fluctuations $$$\mathbf{L}$$$, and $$$\lambda_L$$$ and $$$\lambda_S$$$ trade off data consistency against the low-rankness and sparsity of the estimates of $$$\mathbf{L}$$$ and $$$\mathbf{S}$$$ respectively. Often, an $$$\ell_1$$$-norm is used to enforce sparsity in the solution. Here, we propose the addition of a grouped sparsity constraint, which assumes that groups of voxels show neuronal activity6,7 $$$\Omega(\mathbf{S}) = \rho \| \mathbf{S}\|_1 + (1-\rho) \| \mathbf{S} \|_{2,1},$$$ where $$$\rho$$$ balances the tradeoff between sparsity and the grouping of voxels. SPLORA is solved with FISTA8.

Methods

Data and paradigm: Five subjects were scanned (3T Siemens PrismaFit, multi-band multi-echo GE-EPI, 340 scans, 52 slices, Partial-Fourier=6/8, voxel-size=2.4x2.4x3mm3, TR=1.5s, TEs=10.6/28.69/46.78/64.87/82.96ms, flip-angle=70º, MB-factor=4, GRAPPA=2) while performing a fast event-related general-domain localizer task (Fig1)9,10.
Preprocessing: Motion realignment, geometric distortion correction, smoothing (FWHM=5mm), detrending up to 5th order polynomials, and computation of signal percentage change.
Data analysis: Datasets were analyzed with the proposed SPLORA approach (setting $$$lambda_S$$$ based on the noise estimate of the 3rd TE data, $$$lambda_L$$$ to keep the largest eigenvalues with a relative difference of at least 10%). SPLORA was compared with a session-based GLM (p<0.001), trial-based GLM maps (p<0.05), and a multi-echo multivariate PFM (ME-MvPFM) algorithm (setting $$$lambda_S$$$ based on the noise estimate of the 1st TE data).

Results

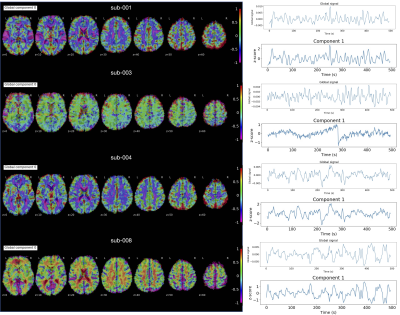
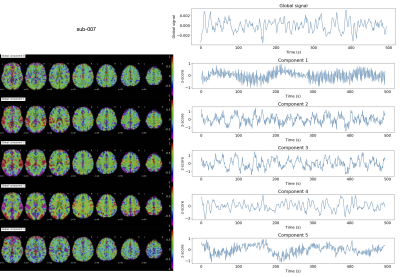
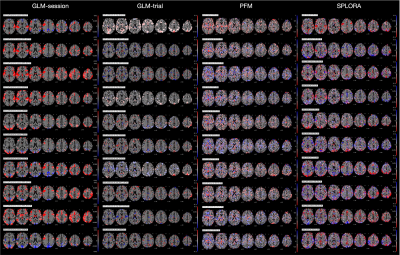
The grayplots11 obtained with the proposed SPLORA approach shows a denoised BOLD signal that is smoother (as expected due to temporal hemodynamic blurring) than the one obtained with ME-MvPFM (Fig2). The grayplot of the global fluctuations concurrently estimated by SPLORA depicts synchronous changes to the large events observed in the motion and DVARS traces (e.g. see deep breath at ~200s, and motion-related plus respiration event at ~300s). The spatial and temporal signatures of the global components estimated by SPLORA for subjects sub-001, sub-004, and sub-006 (one per subject) were highly correlated with their corresponding global (i.e. average-brain) signal, showing evident uniform patterns across the brain (Fig3). Meanwhile, the low-rank component estimated for subject sub-003 exhibited an abrupt signal change that resulted from a big head jerk (E-norm>0.45mm at ~280s) and its map depicted the classical ring at the brain’s edge voxels due to head motion (Fig3). Conversely, SPLORA detected 5 global components for sub-007 that correspond to vascular fluctuations (components 1 and 5) and the task itself (components 2, 3, and 4) (Fig4), suggesting that the task elicited strong widespread BOLD fluctuations and calls for a refinement in the selection of global components. Generally, the single-trial SPLORA activation maps resemble more the session-based GLM maps than those obtained with the trial-based GLM approach, even without knowing their timings, and with ME-MvPFM (Fig5). The trial-based GLM approach struggles to map the brain’s response to each trial correctly due to insufficient degrees of freedom in this fast event-related paradigm; a limitation that is overcome owing to the regularization used in SPLORA and ME-MvPFM. However, ME-MvPFM activity maps are clearly distorted in inferior regions that are prone to susceptibility artifacts, which are separately captured by SPLORA.

Conclusion

Denoising performed by SPLORA with multi-echo fMRI can reduce the effect of global fluctuations that often distort the performance of deconvolution algorithms, without a controversial global signal regression, to blindly decipher the neuronal-related activity underlying individual BOLD events.

Acknowledgements

This research was funded by the Spanish Ministry of Economy and Competitiveness (RYC-2017-21845), the Basque Government (BERC 2018-2021, PIB 2019 104, PRE_2020_2_0227), and the Spanish Ministry of Science, Innovation, and Universities (PID2019-105520GB-100).

References

  1. Power, J. D., Plitt, M., Gotts, S. J., Kundu, P., Voon, V., Bandettini, P. A., & Martin, A. (2018). Ridding fMRI data of motion-related influences: Removal of signals with distinct spatial and physical bases in multiecho data. Proceedings of the National Academy of Sciences, 115(9), E2105-E2114.
  2. Caballero-Gaudes, C., & Reynolds, R. C. (2017). Methods for cleaning the BOLD fMRI signal. Neuroimage, 154, 128-149.
  3. Kundu, P., Inati, S. J., Evans, J. W., Luh, W. M., & Bandettini, P. A. (2012). Differentiating BOLD and non-BOLD signals in fMRI time series using multi-echo EPI. Neuroimage, 60(3), 1759-1770.
  4. Lynch, C. J., Elbau, I., & Liston, C. (2021). Improving precision functional mapping routines with multi-echo fMRI. Current opinion in behavioral sciences, 40, 113-119.
  5. Caballero-Gaudes, C., Moia, S., Panwar, P., Bandettini, P. A., & Gonzalez-Castillo, J. (2019). A deconvolution algorithm for multi-echo functional MRI: Multi-echo Sparse Paradigm Free Mapping. Neuroimage, 202, 116081.
  6. Gramfort, A., Strohmeier, D., Haueisen, J., Hamalainen, M., & Kowalski, M. (2011, July). Functional brain imaging with M/EEG using structured sparsity in time-frequency dictionaries. In Biennial International Conference on Information Processing in Medical Imaging (pp. 600-611). Springer, Berlin, Heidelberg.
  7. Uruñuela, E., Moia, S., & Caballero-Gaudes, C. (2021, April). A Low Rank and Sparse Paradigm Free Mapping Algorithm For Deconvolution of FMRI Data. In 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI) (pp. 1726-1729). IEEE.
  8. Beck, A., & Teboulle, M. (2009). A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM journal on imaging sciences, 2(1), 183-202.
  9. Stefano Moia and Eneko Uruñuela and Vicente Ferrer and César Caballero-Gaudes (2020). EuskalIBUR. OpenNeuro. [Dataset] doi: 10.18112/openneuro.ds003192.v1.0.1
  10. Pinel, P., Thirion, B., Meriaux, S., Jobert, A., Serres, J., Le Bihan, D., ... & Dehaene, S. (2007). Fast reproducible identification and large-scale databasing of individual functional cognitive networks. BMC neuroscience, 8(1), 1-18.
  11. Power, J. D. (2017). A simple but useful way to assess fMRI scan qualities. Neuroimage, 154, 150-158.

Figures

Schematic of the experimental design with the onsets and duration of each condition’s trials (shown with different colors) (a=auditory, v=visual; calc=calculation, mot_left =left-hand finger-tapping, mot_right=right-hand finger-tapping, sent=sentence production, chbh = horizontal checkerboard, chbv = vertical checkerboard).

A) Euclidean norm of realignment parameters (green) and DVARS (gray) time courses for a representative subject (sub-004). Grayplots of the preprocessed data and denoised data (estimate of activity-inducing signal convolved with canonical HRF) using ME-MvPFM. B) Equivalent grayplots using SPLORA which splits the data into global low-rank fluctuations and denoised data. The grayplot of the denoised data obtained with SPLORA shows smoother hemodynamic responses, i.e. less affected by global artifactual events as observed in the motion and DVARS traces, than with ME-MvPFM.

On the left, z-scored spatial signature of the global components estimated by SPLORA for subjects sub-001, sub-003, sub-004, and sub-008. SPLORA found one global component on each of these subjects. On the right, the global (average-brain) signal and the time signature of the global component detected by SPLORA (one per subject). Each pair of global components and global signal time-series corresponds to the spatial signature shown on the left.

On the left, the z-scored spatial signature of the five global components detected by SPLORA for subject sub-007. On the right, the temporal signature corresponds to each of the five global components found with SPLORA. On top, the global (average-brain) signal.

From left to right: activity maps for all 10 conditions in the task calculated with a session-wise general linear model (GLM), single-trial GLM, single-trial multivariate multi-echo paradigm free mapping (PFM), and single-trial SPLORA.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)
0249
DOI: https://doi.org/10.58530/2022/0249