Introduction

In simultaneous multi-slice(SMS) MRI^1-3, multiple slices are simultaneously excited, encoded, and then resolved using coil sensitivity. With SMS imaging with undersampling, image reconstruction typically suffers from inter-slice leakages and in-plane aliasing artifacts. Furthermore, aliasing separation becomes more challenging in case discrepancies between calibration and imaging exist. In this work, to strictly control both inter-slice leakages and in-plane aliasing artifacts in undersampled SMS imaging, we develop a novel, k-space-based one-step solution for SMS MR image reconstruction that optimally exploits variable-density(VD) sampling well suited to extended controlled aliasing and self-calibration from generalized 3D Fourier encoding perspective. Experimental studies are performed to validate the effectiveness of the proposed method in head and knee.

Methods

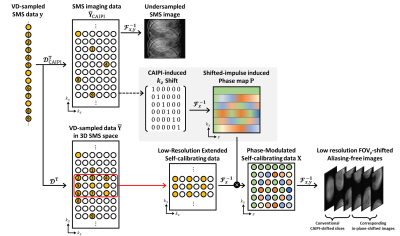
Forward Measurement Signal Model in SMS 3D k-space: A measured VD-sampled SMS data $$$\mathbf{y}$$$ can be expressed by:
$$\mathbf{y}=\mathcal{D}\mathcal{F}_z\mathbf{P}^*\odot\mathbf{X}$$
where $$$\mathcal{D}$$$ is an operator selecting measured samples and reshaping them in SMS 3D k-space;$$$\mathcal{F}_z$$$ is Fourier transform operator along z-direction;$$$\mathbf{P}$$$ is phase-modulation matrix;$$$\odot$$$ is element-wise product;$$$\mathbf{X}=\big\{\mathbf{x}_0,\mathbf{x}_1,\dots,\mathbf{x}_{N_s-1}\big\}$$$ is phase-modulated data of CAIPI-shifted slices;N_s is the number of slices. A CAIPI-measered SMS data can be expressed by: $$\mathbf{y}_\mathrm{CAIPI}=\mathcal{D}_\mathrm{CAIPI}\mathcal{F}_z\mathbf{P}^*\odot\mathbf{X}$$ where $$$\mathcal{D}_\mathrm{CAIPI}$$$ is extraction operator with CAIPI sampling pattern. Extended controlled aliasing, which concatenates in-plane aliased images along the slice direction, is introduced by upsampling both calibration and SMS imaging data in k_y-k_z-space with zero insertion between sampling points in the k_z-direction.
Variable Density Sampling with Extended Controlled Aliasing: A measured SMS 3D k-space with VD sampling $$$\mathbf{y}$$$ is decomposed into one with periodically shifted, regular undersampling(SMS imaging data;$$$\tilde{\mathbf{Y}}=\mathcal{D}^T_\mathrm{CAIPI}\mathbf{y}$$$) and the other with full sampling for low frequency signals(self-calibrating data;low-frequency of $$$\mathcal{D}^T\mathbf{y}$$$), as shown in Fig.1. A CAIPI condition with a linear FOV shift in the slice direction is embedded in the former, while no CAIPI condition is imposed in the latter. To match the CAIPI condition between the two data sets, linear cyclic phase modulation is then applied to the calibration data in k_y-z space slice by slice. Note that phase map $$$\mathbf{P}$$$ is estimated by inverse Fourier transform of CAIPI-induced shift in SMS imaging data.
Modified Hankel Subspace Learning with Extended Self-Calibration: To strictly control both inter-slice leakages and in-plane aliasing artifacts in undersampled SMS imaging, extended self-calibration including both conventional CAIPI-shifted slices and corresponding in-plane-shifted images is performed, in which a slice-specific null space operator is estimated by using modified Hankel subspace learning⁵(mHSL) that explicitly controls not only signal passing in a slice of interest but also signal nulling in its outer slices. The corresponding slice-specific, complementary null space operator for the z^th slice $$$\mathcal{N}^c_z$$$ is estimated by $$$\Big[\mathcal{H}\left (\textbf{x}_{1} \right ), \cdots, \mathcal{H}\left ( \textbf{y}_{\mathrm{CAIPI}} \right ) - \mathcal{H}\left ( \textbf{x}_{z} \right ), \cdots, \mathcal{H}\left ( \textbf{x}_{N_s} \right )\Big]^T\mathcal{N}^c_z =0$$$ where $$$\mathcal{H}$$$ is the Hankel operator.
One-step k-space based Reconstruction for Undersampled SMS Imaging:
To jointly resolve slice separation and in-plane aliasing artifacts in a single step, image reconstruction with the upsampled SMS imaging data is formulated as a constrained optimization problem by balancing null space reconstruction consistency with Hankel-structured low rank prior while enforcing slice-specific data fidelity in SMS 3D k-space with VD sampling:
$$\hat{\textbf{X}}=\arg\min_{\textbf{X}}\sum_{z=0}^{N_s-1}\Bigg[\frac{1}{2}\left\Vert\Big(\mathcal{H} \left( \mathbf{y}_{\mathrm{CAIPI}} \right)-\mathcal{H}\left ( \textbf{x}_\mathrm{z} \right)\Big) \mathcal{N}^c_z \right\Vert_{\mathrm{F}}^{2} + \lambda_L\left\Vert\mathcal{H} \left( \textbf{x}_{\mathrm{z}} \right )\right\Vert_{*} \Bigg]\quad s.t.\quad \mathbf{y}= \mathcal{D} \mathcal{F}_z \mathbf{P}^* \odot \mathbf{X} $$
where $$$\left \| \cdot \right \|_{*}$$$ is the nuclear norm or the sum of singular values of the matrix; $$$\mathrm{\lambda_L}$$$ is the regularization parameter. This is solved using variable splitting methods under the framework of alternating direction approach.
SMS Data Acquisition: A set of T₂-weighted brain data were acquired in a volunteer on a 3T whole-body MR scanner (uMR770, UIH, Shanghai) using single-band(SB) multi-shot FSE for retrospective SMS simulation studies. A set of PD-weighted knee data were acquired using multi-band(MB) multi-shot FSE for prospective studies. An additional set of SB data was acquired using conventional GRE to emulate different image contrasts between calibration and imaging. In all studies, SMS=3, R(in-plane acceleration)=2, CAIPI=3. The imaging parameters in brain FSE were: TR/TE=6000/104ms,flip angle=105°,ETL=16,slice thickness=5mm,matrix size=256x256x3,the number of coils=17. Those specific to the prospective studies were: TR/TE=2000/42.4ms,flip angle=150°,ETL=6,slice thickness=3mm,matrix size=320x240x3,the number of coils=12. For the prospective studies, external calibration data were acquired using conventional GRE, while self-calibrating data were acquired in line with imaging data by adjusting phase encoding blips.

Results

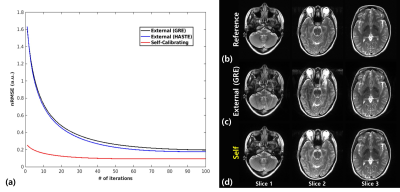
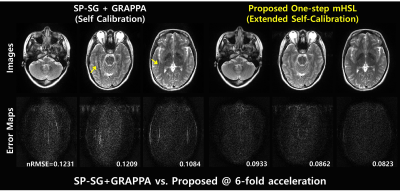
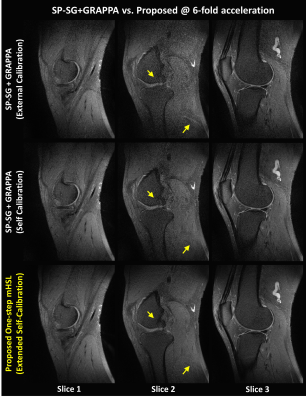
Fig.2 illustrates the dependence on the calibration data image contrast. With self-calibration, nRMSE of proposed one-step mHSL converges faster than that with external calibration(Fig.2a). Images with external calibration are contaminated by aliasing artifacts(Fig.2c), while those with self-calibrating are relatively clean(Fig.2d). Fig.3 compares the proposed method with the SP-SG⁶ followed by GRAPPA by representing reconstructed images and the corresponding error maps using the simulated data with self-calibration. The proposed method exhibits robust suppression of artifacts and noise while the SP-SG still suffers from remaining artifacts. Fig.4 demonstrates the effectiveness of the proposed method in suppressing artifacts and noise using the prospective SMS data.

Discussion and Conclusion

We successfully demonstrated the robustness of the proposed one-step k-space based reconstruction with VD sampling strategies from 3D Fourier encoding perspective in the presence of in-plane undersampling compared to two-step split slice GRAPPA. It is expected that the proposed SMS method would widen its clinical applications, although it needs to be further investigated.

Acknowledgements

This work is supported by NRF-2018M3C7A, KMDF-202011B35, and KMDF-202011C20. we appreciate Dr. Guobin Li (United imaging healthcare, Shanghai, China), Chaohong Wang (United imaging healthcare, Shanghai, China) and Shasha Yang (United imaging healthcare, Shanghai, China) for providing in vivo SMS data.