0237
Receive Array Coil-driven Eddy Current Correction of Diffusion Weighted MRI Data1Melbourne Brain Centre Imaging Unit, The University of Melbourne, Melbourne, Australia, 2Department of Biomedical Engineering, The University of Melbourne, Melbourne, Australia, 3Melbourne Neuropsychiatry Centre, The University of Melbourne, Melbourne, Australia, 4Department of Medicine, The University of Melbourne, Melbourne, Australia, 5Department of Radiology, Royal Melbourne Hospital, Melbourne, Australia, 6MR Research Collaborations, Siemens Healthcare Pty Ltd, Australia, 7Department of Neuroscience, Central Clinical School, Monash University, Melbourne, Australia, 8Department of Radiology, Alfred Hospital, Melbourne, Australia, 9Department of Medicine and Radiology, The University of Melbourne, Melbourne, Australia
Synopsis
An eddy current correction algorithm is proposed that exploits the spatially distributed nature of the receive coil array with signal acquisition immediately preceding image readout in PGSE-EPI diffusion-weighted imaging. The array coil phase for each diffusion gradient direction is expanded using spherical harmonics to yield an estimate of the eddy current-induced field shift in the FOV, and the resultant eddy current-induced pixel shift maps. Distortion corrected diffusion-weighted images are subsequently produced using the estimated pixel shift maps for each diffusion direction, with the method demonstrated in phantom and in-vivo 7T experimental data.
Introduction
A significant source of artifact in diffusion-weighted MRI (DWI) are the eddy currents generated by the long diffusion-sensitizing gradients in the conducting surfaces of the scanner. As has been well characterized, the induction of eddy currents causes deviation in the local magnetic field, resulting in image shear, shift or contraction that can result in misregistration in DWI datasets, causing diffusion index miscalculations1, 2. Eddy currents produce effects that vary across the image volumes, specific to each gradient direction and magnitude1.Dynamic field monitoring using field cameras has been implemented during Pulsed Gradient Spin- Echo (PGSE)-EPI acquisition, to measure the field evolution by monitoring the probe sample’s accrued phase. The eddy current induced fields are estimated by spherical harmonic expansion of the phase recorded by the field camera array, and utilized in a higher order reconstruction to overcome the effects of spatiotemporal field perturbations3, 4, 5, 6, 7.
Although the use of field cameras has shown promising results in quantifying dynamic field evolution and correcting eddy current induced distortion compared to the registration-based and predictive methods, NMR probes are not routinely accessible. In this work, we demonstrate that receive array coils can operate analogously to field cameras, measuring the evolving field immediately before the EPI readout. The coils, distributed in space, measure phase evolution from which eddy current induced field shifts can be estimated for each applied diffusion gradient, with subsequent image distortion correction. We demonstrate receive array coil-driven distortion correction in experimental PGSE-EPI phantom and in-vivo datasets.
Methods
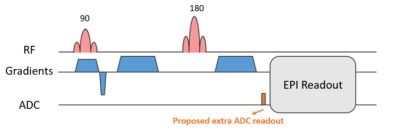
Theory: The signal received by the $$$v^{th}$$$ array coil is$$S_v(t)=\int{\rho(r)C_v(r)e^{j\phi(r,t)}},$$where $$$\rho(r)C_v(r)$$$ is the coil sensitivity-weighted magnetization. The phase function, $$$\phi(r,t)$$$ can be expanded as$$\phi(r,t)=\sum_{l=1}^{N}{K_l(t)h_l(r)},$$where $$$h_l(r)$$$is the $$$l^{th}$$$of $$$N$$$ spherical harmonic bases and $$$k_l(t)$$$are the expansion coefficients4, 7. Given measured array coil signals, the above equations are solved to jointly estimate the expansion coefficients and the field evolution. The difference between the estimated field evolution in a diffusion weighted image and the b0 image provides the eddy current induced field shift due to the specific diffusion gradient.Sequence design: A 2D-EPI unipolar PGSE diffusion sequence was modified to include a 1.5ms ADC readout immediately preceding the EPI readout (Figure 1). The extra readout was short enough to have minimal effect on the minimum echo time achievable by the sequence, but long enough to capture the phase evolution in the array coils.
Experimental data: A bottle phantom containing $$$Ni_2SO_4$$$ and a 24-year-old healthy volunteer were scanned on an investigational 7T whole-body MRI scanner (MAGNETOM 7T plus, Siemens Healthcare, Erlangen, Germany) with a 1Tx/32Rx head coil (Nova Medical Inc.) with the following parameters: FOV 220×220 mm, matrix size 128×128, TE/TR= 80/1000 ms, slice thickness 1.6 mm, BW/Pixel = 1860 Hz, in 6 different diffusion gradient directions (b=1000 s/mm2, δ=12.8 ms, and Δ=38.9 ms) and one b0 image.
Distortion correction: For each diffusion direction, the data from the additional ADC readout was used to solve Eq.(1)-(2) with 2nd-order 3D spherical harmonics5, 7 utilizing a BOBYQA7, 8 optimizer in MATLAB. The eddy current induced field shift and the resultant pixel shift maps in the phase encoding direction were generated. An interpolation algorithm was used to correct the diffusion weighted images.
Results
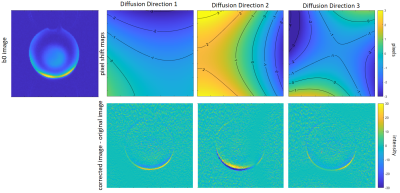
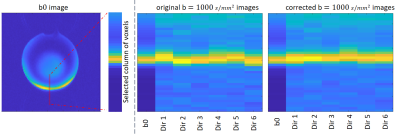
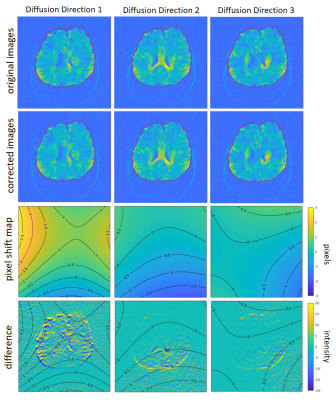
Phantom experiment: The b0 image and estimated pixel shift maps for three exemplar diffusion directions demonstrate the effect of eddy currents (Figure 2), with the difference maps (Figure 2 bottom row) displaying the difference between the corrected diffusion-weighted images and the original diffusion-weighted images. The pixel maps show that the uncorrected images are prone to up to three voxels shift in the phase encoding direction. Figure 3 shows side-by-side images of a selected column of voxels for the b0 image and the 6 diffusion-weighted images. The corrected images show clearly improved alignment in the dataset.in-vivo experiment: Figure 4 shows the original diffusion weighted images (top row), and the corrected images (second row), and the b0 image contour (red lines). The corrected images show improved alignment with the b0 image. The pixel shift maps are illustrated in the third row. The fourth row shows the difference images overlaid with pixel shift contours, which highlights the spatially-varying effects of eddy currents on diffusion weighted images.
Discussion and Conclusion
An eddy current artifact reduction method based on additional signal readout immediately preceding EPI readout, utilising the data from the spatially distributed coils in the receive array coil, has been proposed. The proposed method generates eddy current-induced field shift maps using the signals from the array coil, akin to the sensitivity of the results generated using field cameras, where pixel displacements of -3.3 to 3.3 mm were reported for unipolar PGSE-EPI6. Our results show successful proof-of-concept correction of geometric distortions in phantom and in-vivo experiments, using the readily available array coils and avoiding the cost of field cameras. Future work includes application of the method to higher b-value datasets and demonstration of the impact of the distortion correction on derived diffusion metrics.Acknowledgements
We acknowledge the facilities, the scientific and technical assistance of the Australian National Imaging Facility, a National Collaborative Research Infrastructure Strategy (NCRIS) capability, at the Melbourne Brain Centre Imaging Unit of the University of Melbourne. The work is supported by a research collaboration agreement with Siemens Healthineers.References
1. Jezzard, Peter, et al. "Characterization of and correction for eddy current artifacts in echo planar diffusion imaging." Magnetic Resonance in Medicine 39.5 (1998): 801-812.
2. Graham, Mark S., et al. "Realistic simulation of artefacts in diffusion MRI for validating post-processing correction techniques." NeuroImage 125 (2016): 1079-1094.
3. De Zanche, Nicola, et al. "NMR probes for measuring magnetic fields and field dynamics in MR systems." Magnetic Resonance in Medicine 60.1 (2008): 176-186.
4. Barmet, Christoph, et al. "Spatiotemporal magnetic field monitoring for MR." Magnetic Resonance in Medicine 60.1 (2008): 187-197.
5. Wilm, Bertram J., et al. "Diffusion MRI with concurrent magnetic field monitoring." Magnetic Resonance in Medicine 74.4 (2015): 925-933.
6. Chan, Rachel W., et al. "Characterization and correction of eddy-current artifacts in unipolar and bipolar diffusion sequences using magnetic field monitoring." Journal of Magnetic Resonance 244 (2014): 74-84.
7. Wilm, Bertram J., et al. "Higher order reconstruction for MRI in the presence of spatiotemporal field perturbations." Magnetic Resonance in Medicine 65.6 (2011): 1690-1701.
8. Powell, Michael JD. "The BOBYQA algorithm for bound constrained optimization without derivatives." Cambridge NA Report NA2009/06, University of Cambridge, Cambridge (2009): 26-46.
9. Wallace, Tess E., et al. "Head motion measurement and correction using FID navigators." Magnetic Resonance in Medicine 81.1 (2019): 258-274.
Figures