Introduction

Trans-arterial radioembolization with yttrium-90 microspheres (TARE with Y90) has been widely adopted as a primary trans-arterial locoregional treatment for patients with hepatocellular carcinoma (HCC). Evaluation of lung shunting fraction (LSF) is a key step in Y90 treatment planning. Currently LSF estimation requires a pre-treatment invasive arteriogram using Technetium-99m macroaggregated albumin (Tc-99m MAA) injected into the hepatic artery using single photon computed emission tomography (SPECT) scans to determine the amount of Tc-99m MAA inside lungs^1,2. This LSF estimation requires a dedicated hepatic artery catheterization that doubles the costs in time, expense, and risk to patients. Currently, there is no noninvasive method to estimate LSF. A more cost-efficient, safer, and radiation-free LSF estimation is needed for further development of Y90 therapy. We propose to predict LSF from noninvasive dynamic contrast enhanced (DCE) MRI using perfusion quantification (PQ). Two PQ methods were used to process DCE MRI in 25 patients with HCC: Kety’s tracer kinetic modeling with a delay-fitted global arterial input function (AIF) and quantitative transport mapping (QTM) based on the inversion of transport equation using spatial deconvolution.

Methods

25 patients with HCC were enrolled. Diagnosis was determined based on the Liver Imaging Reporting and Data System (LIRADS)³. All the patients underwent trans-arterial radioembolization therapy utilizing Y-90 resin or glass microspheres. LSF was calculated from a single photon computed emission tomography (SPECT) scan after Tc-99m-macroaggregated albumin (MAA) administration^4,5. Before Y90 treatment, the patients were scanned on a 1.5T scanner with contrast enhanced 3D CAIPI-VIBE sequence⁶ with imaging parameters: in-plane resolution 0.84mm, slice thickness 3mm, temporal resolution 5s, repetition time 4.68ms, echo time 2.39ms, flip angle 10°.
Tracer concentration spacetime resolved imaged were estimated from relative enhancement of DCE MRI using a linear relationship⁷, and were then processed using quantitative transport mapping (QTM) and traditional kinetic modeling method. In QTM, tracer concentration was modeled by a transport equation^8,9:
$$-\triangledown \cdot c(\boldsymbol r,t)\boldsymbol u(\boldsymbol r)=\partial_t c(\boldsymbol r,t) \quad [1] $$
Here $$$\partial_t$$$ is the time derivative, $$$\triangledown=(\partial_x,\partial_y,\partial_z)$$$ the gradient operator, $$$ c(\boldsymbol r,t)$$$ the tracer concentration scalar field at a voxel with index $$$\boldsymbol r = (r_x,r_y,r_z)$$$ in a volume of size $$$N_x,N_y,N_z$$$, and time index $$$t\subseteq { \left\{ 1,2,...N_t-1 \right\}}$$$ the time index with $$$N_t$$$ as the number of time frames. $$$\boldsymbol u (\boldsymbol r)= (u^x(\boldsymbol r),u^y(\boldsymbol r),u^z(\boldsymbol r))$$$ is an velocity vector field. Both time derivative and gradient operator are implemented using finite differences. Eq.1 is solved using ADMM with L1 total variation regularization (regularization parameter $$$\lambda=10^{-4}$$$ ):
$$u=argmin_u\sum_{t=1}^{N_t-1}||\partial_tc+\triangledown \cdot c\mathbf{u}||_2^2 + \lambda ||\triangledown\mathbf{u}||_1 \quad [2] $$
In traditional Kety’s tracer kinetics (also known as extended Tofts’ model), the tracer concentration was modeled by¹⁰:
$$\partial_tc(\boldsymbol r,t)=K^{trans}{\boldsymbol r}[c_a(t-\tau)-\frac{1}{V_e(\boldsymbol r)}c(\boldsymbol r,t)] \quad [3] $$
where $$$c_a(t) $$$ is the global AIF, $$$K^{trans}$$$ is volume transfer constant, $$$V_e(\boldsymbol r)$$$ is the volume fraction of extravascular extracellular space (EES), and $$$\tau$$$ is traveling delay. A voxel wise non-linear least square method is used Eq. 3 with additionoal regularization:
$$ K^{trans},K_{ep},\tau=argmin_{K^{trans},K_{ep},\tau}\sum _{t=1}^{N_t-1}||\partial_tc-K^{trans}c_a(t-\tau)+K_{ep}c||_2^2+\lambda ||\triangledown K^{trans}||_1 + \mu||\triangledown K_{ep}||_1 \quad [4] $$

where $$$\lambda$$$=$$$\mu$$$ = 10^-3(chosen according to the L-curve method¹¹) and $$$K_{ep}=\frac{K^{trans}}{V_e}$$$. For each patient, an experienced radiologist drew the AIF in the feeding artery of the tumor, and manually segmented regions of interest (ROI) consisting of the carcinoma that Y-90 radioembolization treated. $$$|\boldsymbol{u}|$$$, $$$K^{trans}$$$, $$$V_e$$$and $$$\tau$$$ were averaged over these ROIs.

The patients were separated into 2 groups: a low risk group (LSF<10%) and a high risk group (LSF≥10%). Mann-Whitney U tests were performed to compare parameters between low and high risk groups. A receiver operating characteristic curve (ROC) analysis was performed to investigate the risk prediction performance of all parameters. Spearman correlation test was performed to test the relationship between these parameters and lung shunting fraction.

Results

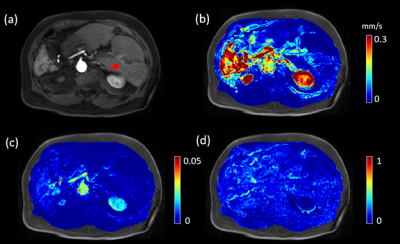
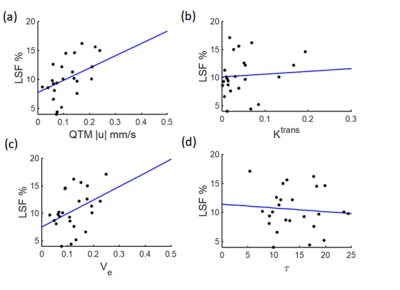
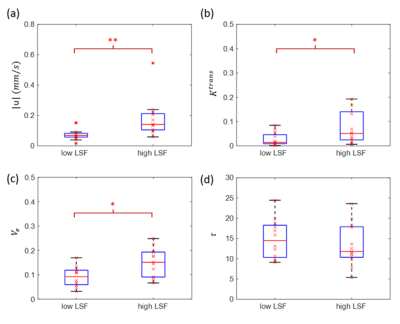
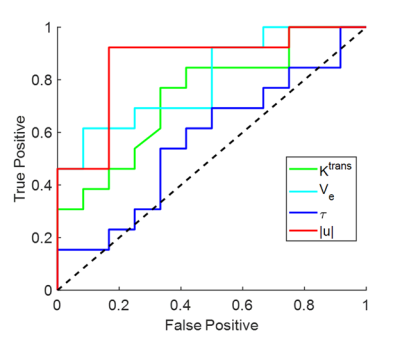
A representative post contrast DCE MRI image of a 74 years old low LSF patient (LSF=9.3%) is shown in Figure 1a. The lesion was well enhanced on post contrast DCE MRI image (red arrow). $$$|\boldsymbol{u}|$$$ , $$$K^{trans}$$$ and $$$V_e$$$ maps are shown in Figure 1b-d, respectively. $$$|\boldsymbol{u}|$$$was positively correlated with LSF (R²=0.3790, F=14.0363, p=0.0011). No significant relationship was found for$$$K^{trans}$$$ (R²=0.0772, F=1.9251, p=0.1786), $$$V_e$$$ (R₂=0.1549, F=4.2168, p=0.0506) and $$$\tau$$$ (R²=0.0078, F=0.1815, p=0.6741). Mann-Whitney U tests indicated differences between the low and high LSF risk groups for $$$|\boldsymbol{u}|$$$ (0.0760 ± 0.0440 vs 0.1822±0.1225 mm/s, p=0.0011), $$$K^{trans}$$$ (0.07±0.04 vs 0.07±0.06, p=0.04) and $$$V_e$$$ (0.0900±0.0307 vs 0.1495±0.0485, p=0.0114). No significant difference was found for $$$\tau$$$ (14.43±3.86 vs 13.12±3.87s, p=0.5679). $$$|\boldsymbol{u}|$$$ gave rise to the highest AUC value (AUC=0.86), followed by $$$V_e$$$ (AUC=0.80), $$$K^{trans}$$$ (AUC=0.74), and $$$\tau$$$ (AUC=0.57). A correlation plot, box plot for the U test, and ROC curve are shown in Figures 2-4, respectively.

Discussion and Conclusion

This study demonstrated the feasibility of using QTM for LSF prediction based on noninvasive pretreatment DCE MRI data. QTM velocity $$$|\boldsymbol{u}|$$$ showed the highest correlation with LSF ($$$R^2=0.3790$$$), following volume fraction $$$V_e$$$($$$R^2=0.1549$$$); $$$|\boldsymbol{u}|$$$ and $$$V_e$$$ can distinguish low LSF and high LSF patients with good accuracy (AUC=0.86 and 0.80, respectively). Future work should include enlarging the dataset and exploring the LSF prediction accuracy of the combination of DCE MRI and other MR modalities to further improve the model performance.

Acknowledgements

No acknowledgement found.