Introduction

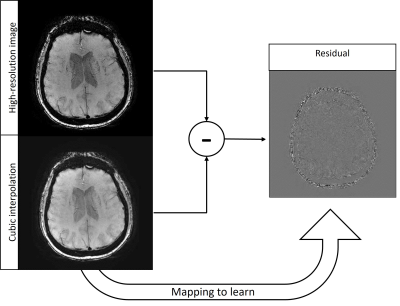
Susceptibility-weighted imaging (SWI) is a method in magnetic resonance imaging (MRI) that visualizes field-distorting compounds in the brain such as calcium deposits or iron found in blood products. The sensitivity of this contrast to venous blood makes SWI useful in cases of traumatic brain injury or stroke [1]. Additionally, SWI allows the detection of microbleeds linked to COVID-19, multiple sclerosis and vascular dementia [2]. In such cases, reducing acquisition time allows rapid intervention [3], as the time penalty for a scan increases proportionally with phase encodes [4]. Given the compromise between resolution and acquisition time, learning the mapping between low and high-resolution images (known as super-resolution) is of interest. Super-resolution of MRI datasets has been achieved with generative adversarial networks (GANs) [5] and convolutional neural networks (CNNs) [6]. Since different contrasts in MRI visualize different anatomical structures, the mappings learned are contrast-specific and there is benefit in examining the mapping between low and high-resolution SWI datasets. While super-resolution approaches can exploit different MRI contrasts as a prior [7], the learned mapping is confined to the contrasts present in the training dataset, which has yet to include SWI. In addition to the clinical value of increasing resolution without extending acquisition time, super-resolved SWI can improve the segmentation of microbleeds to measure the progression and severity of dementia and trauma, respectively [8].
The network architecture in this work is a Very Deep Super Resolution (VDSR) neural network [9], the goal of which is to learn the mapping from a downsampled high-resolution image (i.e. a low-resolution image) and its residual. The residual (Figure 1) is defined as the difference in the high-resolution image and the cubic interpolation of the downsampled image and consists of features that cubic interpolation fails to represent. Learning the residual image rather than the high-resolution image requires less memory and allows faster convergence of stochastic gradient descent. Additionally, learning the residual rather than the high-resolution image produces a robust mapping offering comparable performance on data outside the training distribution, demonstrated in super-resolution at various field strengths despite lack of representation in training data. This multi-field Susceptibility-Weighted Image Super-Resolution is termed SWISeR.

Methods

Training the network amounts to minimizing the loss function $$$E_R(\theta)$$$
$$E_R(\theta) = \frac{1}{2}[(h_{\theta}(x)-y)^2+\lambda(w^Tw)]$$
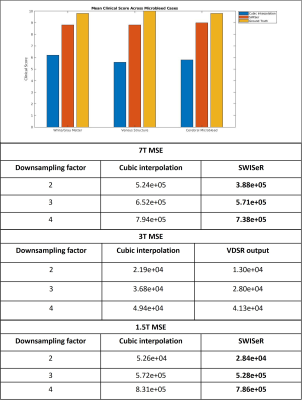
Where $$$\theta$$$ represents the network parameters, $$$h_{\theta}(x)$$$ is the learned residual between the cubic interpolation of the downsampled input $$$x_0$$$ and the high-resolution image and $$$y$$$ is the ground truth residual; $$$\lambda$$$ is an L2 regularization parameter that prevents outsized influence of a particular filter kernel in weight vector $$$w$$$. The VDSR network architecture is comprised of alternating convolution and Rectified Linear Unit (ReLU) layers with a final regression layer. The network depth totals 41 layers, 20 convolution layers with filter size 3 x 3 x 3 and stride of [1 1 1], with 20 ReLU layers in addition to the regression layer. The network was trained with a stochastic gradient descent optimizer with a momentum of 0.9 and a gradient threshold of 0.01 for 200 epochs with an epoch interval of 1. The mini-batch size was 64 and training was conducted on a piecewise learning schedule with an initial learning rate of 0.01, a learning rate factor of 0.1, a learn rate drop period of 10 epochs and an L2 regularization factor of 0.0001. Nine cases featuring 3T SWI scans of matrix size 512 x 512 x 152 and voxel size 0.4297 x 0.4297 x 1 mm with echo time TE = 20 ms were acquired and split 7:1:1 into training, testing, and validation subsets. The training and validation sets were divided into 16 x 16 x 32 patches, normalized by z-score. The training volume was downsampled by cropping the center of k-space by a randomly selected factor of 2, 3, or 4. The downsampled volume was cubically interpolated (upsampled) by the same factor. The residual was calculated by subtracting the cubic interpolation volume from the high-resolution volume. The mean-square error (MSE) between the ground truth and super-resolved image (the sum of the cubic interpolation and residual) was calculated and clinical scoring for microbleed cases was conducted to evaluate the white/gray matter quality, venous structures, and cerebral microbleed resolution.

Results

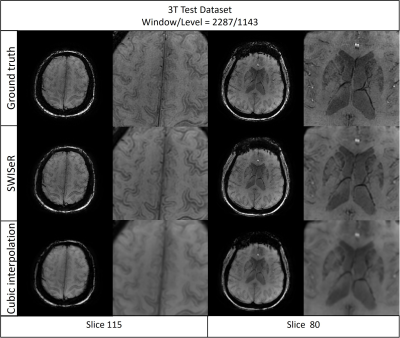
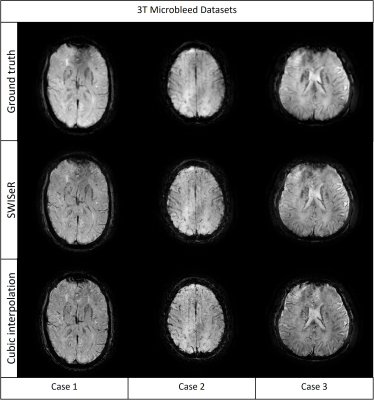
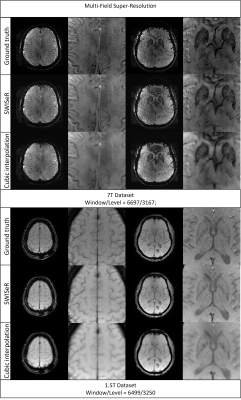
SWISeR outperforms cubic interpolation method at scale factors 2, 3, and 4 on 3T datasets (Figure 2), in both healthy subjects and microbleed cases (Figure 3, 4). This performance generalizes to multiple field strength datasets that had no representation in the training set (Figure 5).

Discussion

Cubic interpolation of the downsampled image results in smoothing corrected by the residual. The super-resolved images have increased detail and sharpness as evidenced by their appearance, MSE and clinical scoring. SWISeR’s performance generalizes across both healthy subjects and microbleed cases, as well as across different field strengths since the learned mapping focuses on the residual image rather than learning the high-resolution image directly. By focusing on the difference between the high-resolution image and the cubic interpolation, SWISeR avoids overfitting to field-specific characteristics of the training dataset.

Conclusion

SWISeR improves visualization of white/gray matter, venous structures, and cerebral microbleeds across various field strengths without requiring additional acquisition time. Future work includes incorporating an auto-encoder to reduce vein blurring in the super-resolved output.

Acknowledgements

No acknowledgement found.