0167
Unsupervised correction network for Nyquist ghost artifact and geometry distortion in echo planar imaging1Korea Advanced Institute of Science and Technology (KAIST), Daejeon, Korea, Republic of, 2Korea Institute of Science and Technology, Seoul, Korea, Republic of
Synopsis
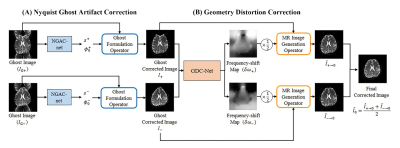
We propose a new correction scheme using a deep neural network with unsupervised learning to correct Nyquist ghosts and geometry distortions occurring in EPI. The proposed scheme includes NGAC-net and GDC-net. First, the NGAC-net estimates the phase error of k-space with the help of a ghost formulation operator and correlation loss. The NGAC-net produces two Nyquist ghost corrected images obtained by dual-polarity phase-encoding gradients. The GDC-net is trained to estimate the frequency-shift map using the two output images from the NGAC-net. Afterwards, an MR image generation operator utilizes the estimated frequency-shift map to obtain the geometry distortion corrected images.
Introduction
Echo planar imaging (EPI) is a fast imaging sequence that was developed to address the slow MR imaging time1. However, EPI is considerably distorted by the field inhomogeneity, resulting in two different types of artifacts: Nyquist ghost artifact and geometry distortion along the phase-encoding direction. However, correcting EPI image distortion is crucial since spatial registration in DTI and fMRI requires undeformed images. Attempts to correct Nyquist ghost artifacts, such as acquiring additional navigator signals and using referenceless methods have been studied2-3. However, these methods require additional imaging time and priori data to correct Nyquist ghost artifacts. To correct geometry distortion, many approaches have been explored such as obtaining field inhomogeneity maps through additional scans, using dual-polarity readout gradients, and applying neural networks4-6. However, these methods require additional imaging time and large training datasets. To counter these issues, Kim et al. developed an unsupervised learning method without labeled data and reduced the correction time by inferencing with the pretrained network. However, this method could only correct mild geometry distortion 7. We attempt to correct both Nyquist artifacts and even severe geometry distortions with unsupervised learning.Method
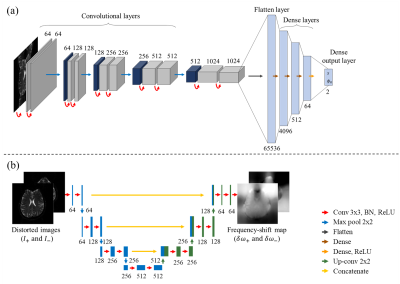
The overall scheme of the proposed method, shown in Fig.1, is composed of two networks: a Nyquist ghost artifact correction network (NGAC-net) and a geometry distortion correction network (GDC-net). The details of the networks are presented in Fig.2. An image acquired with the single-shot spin-echo EPI sequence which has Nyquist ghost artifacts can be written as follows3:$$I_g = I_f\cos(\phi_0+\frac{\pi s}{N_x}x)+iI'_f\sin(\phi_0+\frac{\pi s}{N_x}x)=F_{gh}(I_f,s,\phi_0),\hspace{0.5cm}(1),$$
where $$$F_gh$$$ denotes a ghost formulation operator, $$$I_f$$$ is the ideal ghost-free image, and $$$I'_f$$$ indicates the image shifted with FOV/2 along the phase-encoding direction. Then, the ghost-free image can be obtained with the estimated time delay ($$$s$$$) and constant phase ($$$\phi_0$$$) as follows: $$$I_f=F_{gh}(I_g,-s,-\phi_0)$$$.
By minimizing the correlation coefficient loss function ($$$\mathcal{L_{corr}} = {corr_{I_f}}/{corr_{I_g}}$$$), the NGAC-net is trained to estimate $$$s$$$ and $$$\phi_0$$$ that are used to correct the Nyquist ghost artifact. The $$$corr_{I_f}$$$ is the 2D correlation coefficient between the upper and lower half parts of the image $$$I$$$. Since, $$$corr_{I_g}$$$ has ghost signals along the phase-encoding direction, the $$$corr_{I_g}$$$ is higher than that of the ghost corrected image $$$corr_{I_f}$$$.
As shown in Fig.3A, to generate training datasets for NGAC-net, the Gaussian filtered CIFAR-100 data are used to simulate phase map ($$$\theta$$$), and the ImageNet 2012 data are masked with a brain shape to simulate proton density maps ($$$\rho$$$)8-9.
In previous work, Kim et al. showed that a geometry distortion-free image could be obtained with half of the estimated frequency-shift maps ($$$\delta \omega_+/2,\ \ \delta \omega_-/2$$$) between the two distorted images obtained by dual-polarity phase-encoding gradients ($$$I_+,\ \ I_-$$$)7. The mean absolute error between the input distorted images ($$$I_+,\ \ I_-$$$) and the estimated distorted images ($$$\hat{I_+},\ \ \hat{I_-}$$$), is minimized to optimize the GDC-net for estimating the frequency-shift maps.
Here, unlike the previous work, we use two types of datasets to make the GDC-net able to correct severe geometry distortion. Type 1 is the mild distortion case induced by a smoothed field inhomogeneity map, and type 2 has more severe distortion to simulate local susceptibility effects. The brain-shape masked ImageNet 2012 data are used to represent proton density maps, and the resized and Gaussian filtered CIFAR-100 data are used to represent frequency-shift maps which are induced by the field inhomogeneity effects8-9. As shown in Fig.3B, the frequency-shift maps are smoothed a lot with a Gaussian filter, so that the distortion of the proton density map is mild. Indeed, when EPI images are obtained, the geometric distortion due to the field inhomogeneity is relatively small at the top of the head, whereas slices near the eyes are severely distorted and exhibit large pile up due to the field inhomogeneity generated by large susceptibility difference, such as air in the nasal cavity10. To demonstrate this effect, a type 2 training dataset that had severe pile-up and geometry distortion was prepared as illustrated in Fig.3C.
Results and discussion
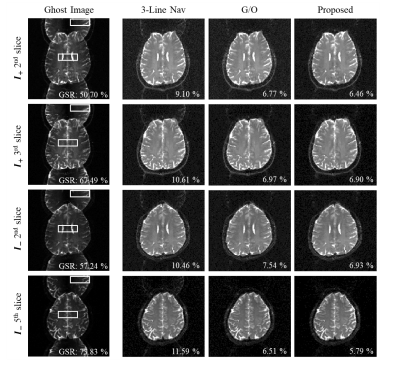
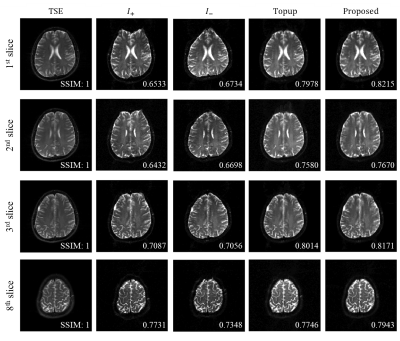
Fig.4 shows the Nyquist ghost corrected images obtained by the 3-line navigator method, the G/O minimization method, and the proposed method. The corrected images acquired from both positive and negative polarity phase-encoding gradients ($$$I_+,\ \ I_-$$$) are shown in Fig.4. A quantitative comparison was made with the ghost-to-signal-ratio (GSR).Fig. 5 shows the geometry distortion-corrected images from the topup11 and the proposed methods. Due to the $$$B_0$$$ field inhomogeneity, the anterior parts of the brains in both $$$I_+$$$ and $$$I_-$$$ are distorted. The anterior of the brain shifts inside for $$$I_+$$$ and outside for $$$I_-$$$. Compared to the turbo spin-echo image, which could be considered as a visually correct ground truth image, the topup and the proposed methods effectively produced geometry distortion-corrected brain images. The proposed method can perform fast computation by utilizing pre-trained weights of the network for the correction of EPI images.
Conclusion
We proposed an unsupervised EPI distortion correction network that did not require labeled images in the training phase. We acquired training datasets by the MATLAB simulation of readily available images such as ImageNet2012 and CIFAR-100. Even though the network has not been trained with MRI data, it successfully works for distortion-corrected EPI images.Acknowledgements
This work was supported by the Korea Medical Device Development Fund grant funded by the Korea government (the Ministry of Science and ICT, the Ministry of Trade, Industry and Energy, the Ministry of Health & Welfare, the Ministry of Food and Drug Safety) (Project Number: 1711138003, KMDF-RnD KMDF_PR_20200901_0041-2021-02).References
1. Poustchi-Amin, M., Mirowitz, S. A., Brown, J. J., McKinstry, R. C., Li, T. Principles and applications of echo-planar imaging: a review for the general radiologist. Radiographics. 21(3), 767-779, 2001.
2. Heid O, inventor; Siemens Healthcare GmbH, assignee. Method for the phase correction of nuclear magnetic resonance signals. US patents 6,043,651. Mar 28, 2000.
3. McKay, J. A., Moeller, S., Zhang, L., Auerbach, E. J., Nelson, M. T., Bolan, P. J. Nyquist ghost correction of breast diffusion weighted imaging using referenceless methods. Magnetic resonance in medicine. 81(4), 2624-2631, 2019.
4. Holland, D., Kuperman, J. M., Dale, A. M. Efficient correction of inhomogeneous static magnetic field-induced distortion in Echo Planar Imaging. Neuroimage. 50(1), 175-183, 2010.
5. P.S. Morgan, R.W. Bowtell, D.J. McIntyre, B.S. Worthington, Correction of spatial distortion in EPI due to inhomogeneous static magnetic fields using the reversed gradient method, J. Magnetic resonance in medicine. 19 (4) (2004) 499–507.
6. Liao, P., Zhang, J., Zeng, K., Yang, Y., Cai, S., Guo, G., & Cai, C. Referenceless distortion correction of gradient-echo echo-planar imaging under inhomogeneous magnetic fields based on a deep convolutional neural network. Computers in biology and medicine. 100, 230-238, 2018.
7. Kim, J., Kwon, K., Kim, B., Kim, S., Park, H. Unsupervised deep learning method for EPI distortion correction using dual-polarity phase-encoding gradients. International Society for Magnetic Resonance in Medicine (ISMRM), 2020.
8. Krizhevsky, A., Hinton, G. Learning multiple layers of features from tiny images. Technical report, University of Toronto, vol.1, No.4, p.7, 2009.
9. Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S., Ma, S., ... Berg, A. C. Imagenet large scale visual recognition challenge. International journal of computer vision. 115(3), 211-252, 2015.
10. Jezzard P, Balaban RS. Correction for geometric distortion in echo planar images from B0 field variations. Magnetic resonance in medicine. 34(1), 65-73, 1995.
11. Andersson, J. L., Skare, S., Ashburner, J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. Neuroimage. 20(2), 870-888, 2003.
Figures