0165
EDDEN: Towards a framework for Evaluating Diffusion MRI DENoising approaches1Sir Peter Mansfield Imaging Centre, Mental Health and Clinical Neurosciences, School of Medicine, University of Nottingham, Nottingham, United Kingdom, 2Precision Imaging Beacon, University of Nottingham, Nottingham, United Kingdom, 3Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States
Synopsis
Denoising diffusion MRI data has gained significant interest over the last years, due to the inherently low-SNR in the dMRI signal. Despite the existence of a number of denoising algorithms, open questions exist on how, and even whether, to denoise data. A consistent set of evaluations that comprehensively characterise newly-developed approaches and their impact on downstream applications is lacking for providing insight to these questions. Here we propose EDDEN, a framework for Evaluating DMRI DENoising approaches, consisting of a set of unique data and assessments. We demonstrate its use using 3 exemplar denoising methods (NLM, MPPCA and NORDIC).
Introduction
Thermal noise is an inherent property of the MRI signal and of any acquired image (1). Modern acquisitions and image reconstruction (for instance, in-plane parallel imaging) can significantly impact noise properties (2,3), leading to challenges in properly characterising statistical properties of the signal. Furthermore, for modalities that rely on signal attenuation, such as diffusion MRI (dMRI), noise can lead to a particularly low signal-to-noise ratio (SNR) and can have a detrimental effect in the signal dynamic range (4,5).De-noising approaches can provide benefits to the above challenges and have hence gained significant interest over the last years, for inherently low SNR dMRI data (6). Such approaches can take advantage of different image properties, for instance: those that rely on a) information redundancy and self-similarity of images (e.g., averaging or NLM and variants (7)), b) information sparseness that can be represented by low-rank, local/patch approximations (e.g., MPPCA (8), NORDIC (9)), and c) unsupervised learning adapted to MRI (e.g.,(10,11)).
Despite the existence of a number of denoising algorithms, open questions exist. Different studies have used different metrics to evaluate algorithms, focusing many times on visual quality (12); but lacking comprehensive quantitative answers on performance or consistency across studies. Importantly, the fundamental question of whether to denoise or not is still debatable. For cases where data are used for biophysical modelling, one would argue that the modelling process itself provides a principled way for separating signal from noise. Furthermore, potential undesired behaviour induced by denoising to downstream applications has not been specifically explored.
Here we propose EDDEN, a framework for Evaluating Diffusion MRI DENoising approaches, providing a set of unique data and assessments, as a minimum, for getting principled answers to the above questions. We demonstrate its application using some exemplar denoising algorithms: NLM, MPPCA, and NORDIC.
Methods
EDDEN DatasetsUsing a 3T Siemens Prisma scanner, we have acquired dMRI data that represent different SNR/resolution regimes.
A) An HCP-style acquisition at 1.5mm isotropic voxels, 270 directions and 3 shells (b=1000/2000/3000 s/mm2). We have 4 repeats of this dataset on the same subject (TR=3.23s/TE=89ms/MB=4).
B) An ultra-high resolution acquisition at 0.9mm isotropic voxels, 199 directions and 2 shells (b=1000/2000 s/mm2) and 3 repeats of the same dataset on the same subject (TR=6.57s/TE=91ms/MB=3/GRAPPA=2).
C) A UK Biobank-style, relatively high-SNR acquisition at conventional resolution of 2mm isotropic voxels, 100 directions and 2 shells (b=1000/2000 s/mm2, TR=3.3s/TE=67ms/MB=3).
EDDEN Assessments
We propose metrics that assess performance of denoising algorithms for dMRI in 6 distinct domains using the above datasets:
1) Gains on raw signal quality, as quantified by SNR and angular contrast-to-noise-ratio (CNR) (13).
2) Effect on signal statistical properties, assessed by a) whether signal undesirably becomes non-Rician after denoising, b) whether noise floor (4,5) is reduced by denoising, c) whether undesirable spatial smoothing/correlations are induced by denoising.
3) Convergence at a high SNR regime to exclude unwanted signal modification when the noise levels are too low.
4) Effect on biophysical modelling performance, assessed by increased precision (and potentially accuracy) in estimates after denoising.
5) Benefits for reducing scan time by a) either reducing number of repeats or b) number of dMRI directions to achieve similar performance as with the full acquisition.
6) Benefits for pushing spatial resolution at ultra-high levels that cannot be achieved without bespoke acquisitions/setups.
Results
We demonstrate how the EDDEN framework can provide insight into performance within different domains of exemplar denoising approaches. Fig.1 assesses the effect on raw signal quality, where denoising is expected to increase signal and contrast-to-noise ratio. All tested approaches do that.At the same time, a denoising approach would ideally preserve the statistical properties of the signal, as these determine validity of assumptions for downstream applications and analysis. Our second set of evaluations assesses whether a noise floor (expected in noisy data(4)) is removed (Fig.2A) and whether smoothing is induced by denoising (Fig.2B).
Improvements in modelling performance are anticipated by a denoising algorithm. Fig.3A demonstrates examples for a crossing-fibre model, where denoising supports more fibre complexity in the centrum semiovale (where majority of voxels contain crossings(14)) and higher precision/less uncertainty in estimation.
Denoising provides opportunities for increasing SNR/time, therefore indirectly reducing scan time needed to achieve certain SNR; by either removing the need for multiple repeats (Fig.4A) or for multiple dMRI directions (Fig.4B). EDDEN data and tests allow performance to be assessed quantitatively in that respect. A qualitative comparison is shown here for fractional anisotropy maps, pre- and post-denoising and how these compare against maps from considerably longer scan times.
Finally, we propose that denoising should open opportunities that only bespoke setups can provide, such as allowing usable data at sub-mm spatial resolution, acquired using a standard clinical system. Fig.5 demonstrates such an example, by achieving good reconstruction of WM tracts after denoising of data, which originally fail to support tract reconstruction.
Discussion & Conclussion
We have presented a set of data and assessments, EDDEN, that allow comprehensive characterisation of performance of dMRI denoising approaches. The answer on whether to denoise or not and how to best do it is not straightforward and many parameters need to be considered. EDDEN objectively evaluates of -what we propose as a minimum of- these parameters.Acknowledgements
JPMP is supported by a PhD studentship funded by the Precision Imaging Beacon of Excellence, University of Nottingham. SS is supported by the Wellcome Trust (217266/Z/19) and a European Research Council consolidator grant (ERC 101000969). SM and EY acknowledge CMRR centre support funding from NIBIB (P41EB027061) and NIH (U01 EB025144).
References
1. Gudbjartsson H, Patz S. 1995. The Rician distribution of noisy MRI data. Magnet Reson Med. 34(6):910–14
2. Dietrich O, Raya JG, Reeder SB, Reiser MF, Schoenberg SO. 2007. Measurement of signal-to-noise ratios in MR images: Influence of multichannel coils, parallel imaging, and reconstruction filters. J Magn Reson Imaging. 26(2):375–85
3. Aja-Fernández S, Vegas-Sánchez-Ferrero G, Tristán-Vega A. 2014. Noise estimation in parallel MRI: GRAPPA and SENSE. Magn Reson Imaging. 32(3):281–90
4. Jones DK, Basser PJ. 2004. “Squashing peanuts and smashing pumpkins”: How noise distorts diffusion‐weighted MR data. Magnet Reson Med. 52(5):979–93
5. Sotiropoulos SN, Moeller S, Jbabdi S, Xu J, Andersson JL, et al. 2013. Effects of image reconstruction on fiber orientation mapping from multichannel diffusion MRI: Reducing the noise floor using SENSE. Magnet Reson Med. 70(6):1682–89
6. Veraart J, Novikov DS, Christiaens D, Ades-aron B, Sijbers J, Fieremans E. 2016. Denoising of diffusion MRI using random matrix theory. Neuroimage. 142:394–406
7. Buades A, Coll B, Morel J-M. 2005. A non-local algorithm for image denoising. 2005 Ieee Comput Soc Conf Comput Vis Pattern Recognit Cvpr’05. 2:60–65
8. Veraart J, Novikov DS, Christiaens D, Ades-aron B, Sijbers J, Fieremans E. 2016. Denoising of diffusion MRI using random matrix theory. Neuroimage. 142:394–406
9. Moeller S, Pisharady PK, Ramanna S, Lenglet C, Wu X, et al. 2021. NOise reduction with DIstribution Corrected (NORDIC) PCA in dMRI with complex-valued parameter-free locally low-rank processing. Neuroimage. 226:117539
10. López MM, Frederick JM, Ventura J. 2021. Evaluation of MRI Denoising Methods Using Unsupervised Learning. Frontiers Artif Intell. 4:642731
11. Fadnavis S, Batson, Garyfallidis. 2020. Patch2Self: Denoising Diffusion MRI with Self-Supervised Learning. NeurIPS
12. Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. 2004. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Transactions on Image Processing. 13(4):
13. Bastiani M, Cottaar M, Fitzgibbon SP, Suri S, Alfaro-Almagro F, et al. 2019. Automated quality control for within and between studies diffusion MRI data using a non-parametric framework for movement and distortion correction. Neuroimage. 184:801–12
14. Jeurissen B, Leemans A, Tournier J-D, Jones DK, Sijbers J. 2013. Investigating the prevalence of complex fiber configurations in white matter tissue with diffusion magnetic resonance imaging: Prevalence of Multifiber Voxels in WM. Hum Brain Mapp. 34(11):2747–66
15. Jbabdi S, Sotiropoulos SN, Savio AM, Graña M, Behrens TEJ. 2012. Model-based analysis of multishell diffusion MR data for tractography: How to get over fitting problems. Magnet Reson Med. 68(6):1846–55
16. Warrington S, Bryant KL, Khrapitchev AA, Sallet J, Charquero-Ballester M, et al. 2020. XTRACT - Standardised protocols for automated tractography in the human and macaque brain. Neuroimage. 217:116923
Figures
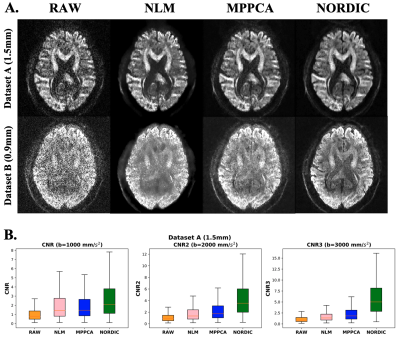
Fig. 1. Assessing effects of denoising on raw signal quality – A) Images pre- and post-denoising (using NLM, MPPCA and NORDIC) for datasets A (1.5mm, b-value=3000s/mm2) and dataset B (0.9mm, b-value=2000mm/s2). B) Angular contrast to noise ratio (CNR) for different b values, pre- and post-denoising.
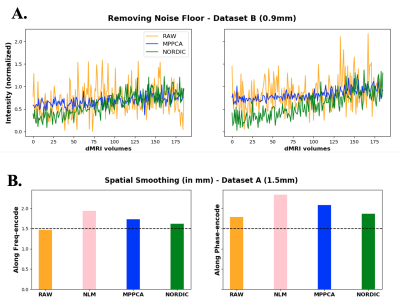
Fig. 2. Assessing effects of denoising on signal statistical properties. A) Removing noise floor. DMRI signals from two high-anisotropy voxels, where a noise floor caused signal rectification. Denoising should remove noise floor and increase the signal dynamic range (e.g. NORDIC). B) Spatial smoothness in DTI model residuals along frequency (x) and phase-encoding (y) directions, pre- and post-denoising.
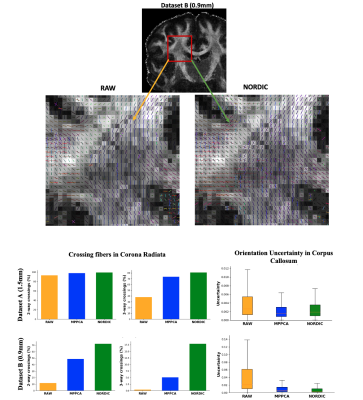
Fig. 3. Effects of denoising on modelling performance. Number of crossing fibres and orientation uncertainty estimates after applying different denoising methods, as estimated by parametric spherical deconvolution (15). Denoising allows more complexity in the centrum semiovale (where most of voxels are expected to contain crossings) and less orientation uncertainty.
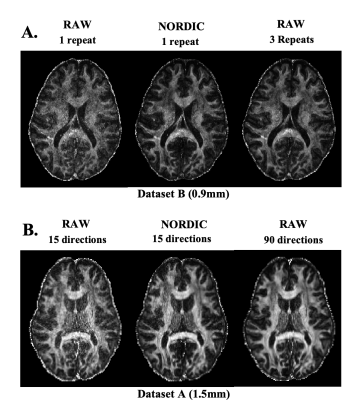
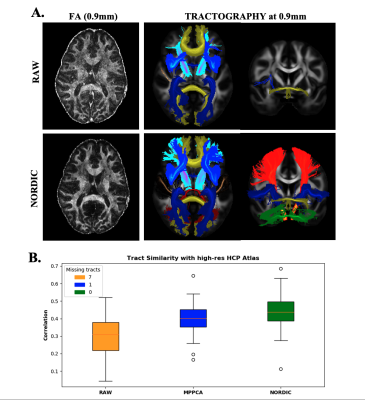
Fig. 5. Assessing effects of denoising on pushing spatial resolution. A) FA map and tracts obtained pre- and post-denoising of ultra-high resolution Dataset B (0.9mm). B) Spatial tract correlation to the high-resolution HCP atlas (16), across 42 WM tracts. The legend reflects the number of missing tracts (noisy raw data did not allow reconstruction of 7 tracts).