Introduction

Magnetization transfer contrast MR fingerprinting (MTC-MRF) is a novel quantitative imaging technique that simultaneously quantifies free bulk water and semisolid macromolecule parameters using pseudorandomized scan parameters^1-3. Recently, a fully connected neural network (FCNN)-based MRF reconstruction² was proposed to quantify multiple tissue parameters by learning the mapping relation between MRF and tissue properties. However, the construction of a huge training dataset is unavoidable when a multi-pool exchange model is to be accounted for in Bloch-McConnell simulations. To improve reconstruction accuracy and generalization performance, the training dataset must be highly sampled with a wide range of tissue parameter combinations, which is extremely computationally expensive. In addition, optimization of the MRF acquisition schedule is very important to accelerate data acquisition and for improved accuracy of the parameter estimation^4,5. However, generating a dictionary or training dataset for each MRF schedule tested incurs a high computational burden, which is impractical. In this study, we developed a unified deep-learning architecture including an ultrafast Bloch simulator and tissue parameter reconstruction. A test-retest study was performed to evaluate reliability of the unified deep-learning framework.

Methods

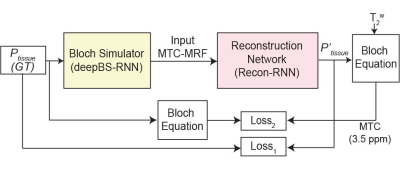
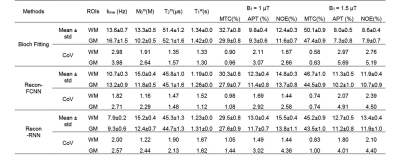
A bi-directional long-short term memory (Bi-LSTM)-based recurrent neural network (RNN) in combination with convolutional neural network- and fully connected neural network (FCNN)-based architectures were designed for the ultrafast Bloch simulator (deepBS-RNN and deepBS-FCNN, respectively). Furthermore, a RNN-based architecture was designed for MRF reconstruction (Recon-RNN) as shown in Fig. 1. The Loss₁ was applied between ground truth and estimated tissue parameters and Loss₂ was applied between estimated MTC signal intensity at 3.5 ppm and corresponding ground truth. The performance of the Bloch simulators and MRF reconstruction was evaluated using numerical phantoms and ten healthy volunteers. The deepBS networks were trained on 2 million data, the ground truth MTC-MRF signals were obtained from conventional Bloch simulation (BS). The MRF reconstruction network (Recon-) was trained on three datasets i.e., data generated from deepBS-RNN, deepBS-FCNN and BS. The size of training dataset for MRF reconstruction was 8 million. The MRF reconstruction network estimated semisolid macromolecular proton to water proton exchange rates (k_mw), concentrations (M₀^m), T₂ relaxation times (T₂^m), free bulk water T₁ relaxation times (T₁^w), and MTC images at ±3.5 ppm (= 1 - Z_ref (±3.5 ppm)) corresponding to RF saturation powers of 1 μT and 1.5 μT that can be used for amide proton transfer (APT) and nuclear Overhauser enhancement (NOE) imaging based on simple subtraction. The semisolid macromolecular proton T₁ relaxation time was set a constant value of 1 s and water T₂ relaxation time was independently measured from a multi-echo sequence. The APT and NOE images were calculated by subtracting Z_ref (±3.5 ppm) from experimentally acquired images at ±3.5 ppm. To measure test-retest reliability, ten healthy volunteers were scanned in two sessions, two weeks apart, using a 3T scanner after informed consent was obtained in accordance with the IRB requirement. Interscan coefficient of variance (CoV) were calculated to quantify reliability.

Results and Discussion

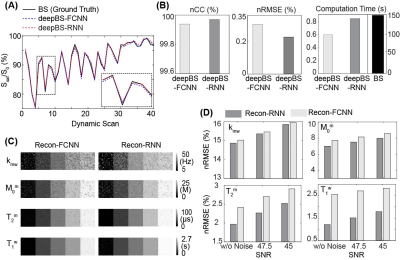
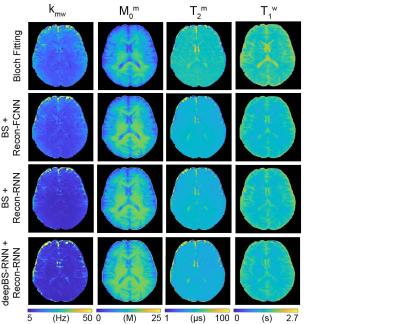
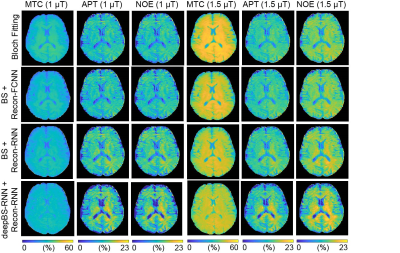
MTC-MRF profiles from the deepBSs were in excellent agreement with the ground truth as shown in Figs. 2A and 2B, but the deepBS-RNN showed higher accuracy than the deepBS-FCNN. Importantly, the deep-learning-based Bloch simulators (deepBS-) achieved significantly higher computation efficiency (by a factor of ~200) than the conventional Bloch simulation (BS). These comparisons were performed on a 10K test dataset. The deep-learning-based MRF reconstructions (recon-FCNN and recon-RNN) were evaluated using numerical phantoms with various SNRs (Figs. 2C and 2D). The nRMSE values of the recon-RNN were overall lower than those of the recon-FCNN over all SNR levels. Quantitative water and semisolid MTC parameter maps (Fig. 3), and corresponding MTC, APT, and NOE images at 1 μT and 1.5 μT (Fig. 4) were successfully obtained in vivo using the deep-learning MRF reconstruction methods trained with the simulation data from the conventional Bloch simulation and the RNN-based deep Bloch simulator. The tissue parameters, and MTC, APT, and NOE signals estimated by the deep-learning MRF reconstructions were in good agreement with values obtained from the Bloch equation fitting approach, but the reconstruction time was reduced ~10,000-fold. The reliability of the deep-learning MRF reconstruction methods was evaluated by a test-retest study (see Table 1). The CoV values for the deep-learning MRF reconstructions were less than 5% for all water, semisolid MTC parameters, MTC, APT, and NOE signals, indicating a high test-retest reliability.

Conclusions

Ultrafast Bloch simulators and MTC-MRF reconstruction methods based on RNN were developed, validated in numerical phantoms, and demonstrated in healthy volunteer human brains. The deep-learning-based Bloch simulator significantly reduced the computation time for generation of training datasets (34 hrs. for Bloch simulation vs. 11 min. for deep-learning Bloch simulator for an 8 million training dataset). The RNN-based MRF reconstruction demonstrated advantages in terms of quantification accuracy and computation efficiency. The test-retest study showed a high degree of reliability of the proposed MTC-MRF framework in brain and holds promise for assessing multiple tissue parameters simultaneously in a single scan.

Acknowledgements

This work was supported in part by grants from the National Institutes of Health.