Introduction

Magnetic resonance elastography (MRE) allows for non-invasive determination of tissue visco-elastic properties, which differ for healthy and diseased tissues. Longitudinal changes in tissue stiffness in the course of pancreatitis, endocrine dysfunction or pancreatic cancer could reveal new insights in the disease pathophysiology[1]. However, assessing the pancreas with MRE remains challenging due to its small size, elongated shape, and central abdominal location. The quantitative accuracy of MRE in small structures depends on the local stability of the tissue being imaged over all wave-offsets and motion-encoding directions. However, current pancreatic MRE requires four consecutive (16s) breath-holds[2]. These may introduce errors in pancreas location, limit spatial and temporal resolution, and can be particularly uncomfortable for patients.

The aim of this study was to develop and test a single breath-hold MRE acquisition accelerated using prospective undersampling and compressed sensing (CS) reconstruction in the pancreas.

Methods

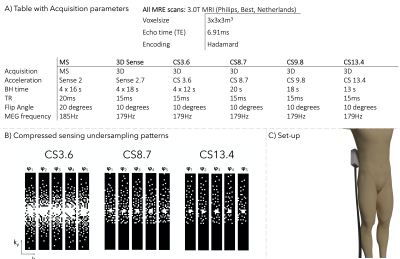
We modified the 3D Ristretto GRE-MRE acquisition to accommodate for compressed sensing acceleration[3,4]. Feasibility of CS-accelerated MRE was first established by retrospective undersampling (factors:R=0-15) and reconstruction of a 3D MRE dataset of a CIRS phantom with inclusions (CIRS,Inc.,Norfolk,USA). Data was acquired by Guenthner et al. using 36Hz vibration frequency and eight wave-phase offsets in 14 slices (FOV:192x156x42mm)[3]. Scan parameters are reported in Figure 1a.

In-vivo testing was performed on six healthy volunteers (female=6, mean age=27±3 years). A gravitational transducer [5] with a 3D-printed curved polyactic-plate was strapped to the right flank at the level of the pancreas head (Figure.1c). High-resolution T2-weighted images were made for anatomical reference. MRE acquisitions were performed using 40Hz vibration frequency, nine slices (FOV:336x192x27mm) and five wave-phase offsets. Six consecutive pancreatic MRE scans were performed: (I)standard Multi-Slice (MS), (II)3D SENSE-accelerated four breath-hold acquisition, (III)3D CS-accelerated four breath-hold acquisition and (IV-VI)three 3D CS-accelerated single breath-hold acquisitions. Scan parameters are reported in Figure 1a.

Incoherent undersampling was achieved using variable-density Poisson disks with half-scan in both k_y (67%) and k_z (89%) directions(Figure.1b). Five different undersampling patterns with different undersampling factors (R=3.6,8.7,9.8,13.4) were used for each wave-phase offset and were repeated for each encoding direction. For CS acquisitions, reconstruction was performed offline using ReconFrame (Gyrotools,Zurich,Switzerland) in MATLAB (MathWorks,Natick,MA,USA) together with the Berkeley Acquisition Advanced Reconstruction Toolbox (BART) using total variation sparsifying transform in the wave-offset dimension (l=0.001, 20 iterations)[6,7,8].

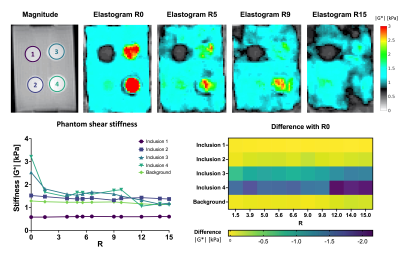
Phantom post-processing was performed using MATLAB. The shear stiffness of each inclusion and background was calculated and compared to the non-accelerated stiffness. In-vivo MRE post-processing was performed using dedicated software(ROOT,KIR). Phase data are unwrapped and smoothed before 3D transformation using a 3D Blackman-Harris window. The shear wave displacement was calculated per voxel and visco-elastic parameters were extracted with a finite element method. Mean shear wave speed (SWS) and shear stiffness (|G*|) were calculated by manually drawn region-of-interest over the pancreatic head and liver on MRE magnitude images guided by anatomical high-resolution T2-weighted images.

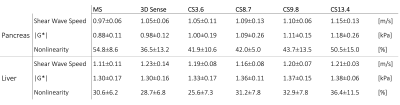
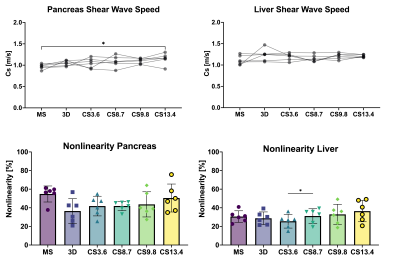
Mean SWS, |G*| and the nonlinearity (ratio of the second harmonic over the first harmonic) in both the pancreas head and liver were analyzed, with 3D-SENSE-MRE allocated as index test for CS. Statistical analysis was done using repeated measures ANOVA and pairwise comparison with a Bonferroni correction(p<.05) for SWS and nonlinearity parameters of the pancreas and liver.

Results

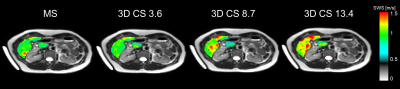
Mean |G*|and example elastograms of the phantom data are shown in Figure 2. In-vivo examples of SWS-maps in the pancreas are shown in Figure 3. The mean SWS, |G*| and nonlinearity for the pancreas and liver are given in Figure 4. Mean SWS and nonlinearity of each method for the pancreas and liver are shown in Figure 5. Repeated measures ANOVA showed no significant differences in SWS overall(f=5/1,p=0.07). Exploratory pairwise comparison showed significant difference between mean SWS of MS and CS13.4(p=.03) in the pancreas and nonlinearity in the liver between CS3.6 and CS8.7(p=.02).

Discussion

Phantom retrospective undersampling showed accurate results for low stiffness inclusions and background (|G*|<1.6kPa) up to an acceleration factor of 15 (Figure.2). However, for the two stiff inclusion the apparent stiffness deviated from non-accelerated R0 values, with underestimation increasing for higher acceleration factors. The relative low mechanical frequency (and hence long wavelength) could explain this disparity[9].

CS-accelerated MRE gave comparable stiffness values in-vivo up to an acceleration factor of 8.7. The nonlinearity showed no significant difference between all scans in the pancreas, indicating that higher acceleration does not significantly hamper visco-elastic reconstruction. However, accuracy of MRE inversion is only guaranteed for a nonlinearity below 50%, therefore CS acceleration of 13.4 (nonlinearity=50.5%) could be considered borderline acceptable.

Liver nonlinearity shows a significant difference between CS3.6 and CS8.7, however, this is not seen for higher acceleration. This could be caused by the large spread observed at CS13.4. A large spread in quality parameters, such as nonlinearity, could indicate loss in accuracy and thereby reproducibility. Additionally, while acceleration of CS=8.7 displayed no difference in SWS and nonlinearity compared to MS, the breath-hold duration (20s) may be too long for some patients.

Conclusion

Phantom and in-vivo testing shows that compressed sensing accelerated, single breath-hold MRE is feasible without hampering visco-elastic reconstruction in tissues with low shear stiffness (|G*|<1.6kPa). Further research is necessary to guarantee accuracy of the measured shear stiffness, notably for high stiffness tissues such as tumors, and at higher acceleration factors.

Acknowledgements

No acknowledgement found.