0101
3D Diffusion-prepared MRF (3DM) with cardiac gating for rapid high resolution whole-brain T1, T2, proton density and diffusivity mapping1Department of Radiology, Stanford university, Stanford, CA, United States, 2Department of Electrical Engineering, Stanford university, Stanford, CA, United States, 3Department of Electrical Engineering and Computer Science, MIT, Cambridge, MA, United States, 4Department of Bioengineering, Stanford university, Stanford, CA, United States, 5Department of Clinical Neuroscience, Karolinska Institute, Stockholm, Sweden
Synopsis
In this work, a diffusion preparation was implemented in a 3D spiral-projection MRF framework to introduce additional diffusion weighting. Using MRF dictionary with diffusion terms, it enables whole-brain T1, T2, PD and additional diffusivity mapping with 1.25-mm isotropic resolution within 3min. To improve the image quality, cardiac gating and low-resolution navigator were also implemented to mitigate the signal variation caused by motion during diffusion encoding. Subspace reconstruction was used along with LLR regularization to improve the reconstruction conditioning as well as SNR.
Introduction
Magnetic Resonance Fingerprinting(MRF)1 is a fast quantitative imaging technique for multi-parameter mapping. Initially developed for T1, T2 and proton density(PD) quantification, MRF has been extended for quantification of other tissue parameters, such as diffusivity2, velocity3, T2*4. Concurrently, several 3D-MRF techniques5–7 have been developed to improve image quality and acquisition speed of MRF. Building on previous works8,9 of 3D-SPI-MRF and subspace reconstruction10, we augment 3D-SPI-MRF with a diffusion-preparation(DP) module, with cardiac triggering11 and navigators to achieve rapid high isotropic resolution whole-brain T1, T2, PD and diffusivity mapping.Method
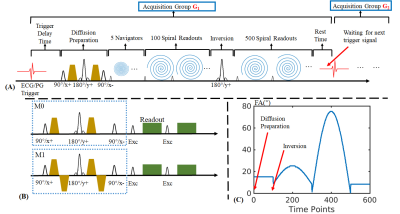
Sequence: Fig1A shows the 3DM sequence diagram where data are acquired across 600 TRs per acquisition group, with multiple groups performed sequentially to achieve adequate 3D k-space encoding. Each acquisition group contains a diffusion-preparation module, an adiabatic inversion preparation, 600 variable-FA acquisitions(shown in Fig1C) with TR=12.5ms and 2s wait time for signal recovery to improve SNR, resulting in a net acquisition per group of 9.5s. For acquisition at 1.25-mm isotropic resolution across FOV of 220×220×220mm3, 36 acquisition groups were obtained in 5min42s, plus additional cardiac trigger waiting time that adds on average ~0.5s to the 9.5s scan time per acquisition group(i.e. only ~5%).With DP, shot-to-shot phase variation from microscopic-motions during diffusion-encoding will cause undesirable magnitude variation in the data. The application of an amplitude stabilizer(dephasing) gradient prior to the tip-up can mitigate this issue at a cost of halving the signal12. With such approach, in the subsequent readout-train, a rephasing gradient is applied prior to each readout to rephase the diffusion-encoded spins. For MRF, such rephasing gradient would also dephase away any signal from the recovering Mz during its long readout train, making such an approach incompatible. Therefore, in our 3DM sequence, a combination of cardiac-gating11 and M1-compensated diffusion-preparation13 are used instead to minimize motion-sensitivity and shot-to-shot amplitude variation. Fig1B shows conventional M0-compensated and M1-compensated14 DP, where M1-compensation help overcome signal variation from constant-velocity motions, at a cost of slightly lengthened preparation time. In this work, b=600s/mm2 was used, resulting in a preparation time of 42ms for M0-compensated and 67ms for M1-compensated DP.
Additionally, to avoid variability in cardiac-trigger signal and/or other abnormal motion causing artifacts, the first five TRs after DP are used to acquire a 3D-navigator at 5-mm isotropic resolution, thus the data of acquisition groups with strong amplitude variations can be excluded from the reconstruction to further improve the reconstruction.
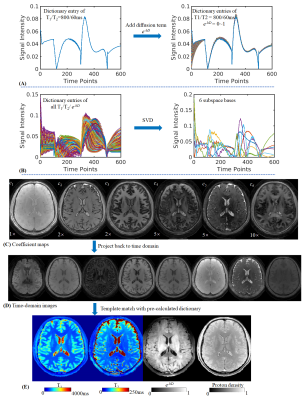
Dictionary: Fig2A shows the dictionary entry for tissue with T1/T2=800/60ms which was calculated using EPG15. With additional diffusion term e-bD(ranging from 0~1), the signal evolution curves show significant difference for different diffusivity, thus enabling the use of dictionary matching to estimate tissue’s diffusivity.
Recon: As Fig2B shows, by applying SVD to dictionary, the first six principal components are extracted as subspace bases(Φ1-6). The coefficient maps(c1-6, Fig2C) are calculated with subspace reconstruction9,10 and locally low rank (LLR) regularization16,17 using the BART toolbox18. Coefficient maps were then used to generate MRF time-series images(Fig2D) and dictionary matching applied to obtain T1, T2, PD and diffusivity maps(Fig2E).
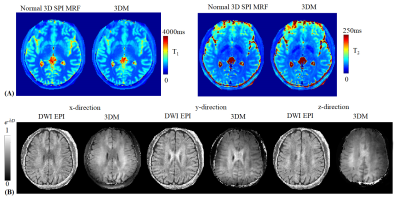
Validation: Two healthy volunteers were scanned on a GE 3T Premier scanner using a 48-channel head coil. In addition to the 3DM acquisition, conventional 3D SPI-MRF was also acquired to validate whether T1 and T2 quantification could be affected by the diffusion preparation. Conventional DWI EPI sequence was also obtained to validate the diffusivity measured of 3DM.
Results
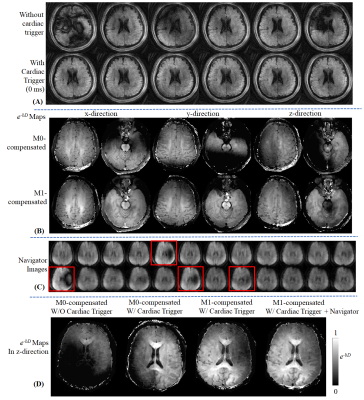
Fig3A shows that the diffusion-prepared 2D-spiral FISP images with 0ms-delayed cardiac gating performed better than those without cardiac gating. In Fig3B, e-bD maps using M0-compensated and M1-compensated didn’t show significant difference in upper slices. However, for bottom slices that were more vulnerable to cardiac-cycle motion, image quality of M0-compendated degraded significantly. Fig3C shows the reconstructed 3D-navigators from the 3DM sequence with Gz diffusion encoding, indicating a small number of remaining acquisition groups with signal voids that needs to be removed(red boxes) for better reconstruction. Note: The strongest signal-variation by far was observed with Gz encoding, as cardiac-motion is most severe in the z-direction19. Fig3D shows the e-bD maps for z-direction diffusion, where the application of cardiac gating, M1-compensated DP and signal removal via navigator progressively improve the image quality.Fig4 compared the performance of the proposed method with a normal 3D SPI MRF scan for T1 and T2 maps(Fig4A), and with a DWI EPI sequence for e-bD maps(Fig4B).
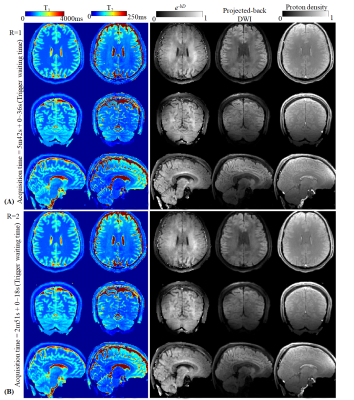
Fig5 shows the quantitative maps measured using the proposed method with ~6 min acquisition time(including waiting time of trigger), and a 2-fold undersampled version with acquisition of 3min. In addition, by projecting the reconstructed coefficient maps from subspace domain to time domain, diffusion-weighted images could also be obtained(fourth column).
Discussion and Conclusion
In this work, we deployed DP in a 3D SPI-MRF sequence to enable whole-brain T1, T2, PD and diffusivity mapping with 1.25-mm isotropic resolution within 3min. To improve the image quality, cardiac gating and low-resolution navigator were also implemented. Subspace reconstruction was used along with LLR regularization to improve the reconstruction conditioning as well as SNR. Future work will incorporate isotropic diffusion encoding20 into the 3DM sequence, which should also enable rapid ADC quantification from a single 3DM scan.Acknowledgements
This study is supported in part by GE Healthcare research funds and NIH R01EB020613, R01MH116173, R01EB019437, U01EB025162, P41EB030006.References
1. Ma, D. et al. Magnetic resonance fingerprinting. Nature 495, 187–192 (2013).
2. Pirkl, C. M. et al. Deep learning-based parameter mapping for joint relaxation and diffusion tensor MR Fingerprinting. 638–654 (2020).
3. Flassbeck, S., Schmidt, S., Bachert, P., Ladd, M. E. & Schmitter, S. Flow MR fingerprinting. Magn. Reson. Med. 81, 2536–2550 (2019).
4. Wang, C. Y. et al. Magnetic resonance fingerprinting with quadratic RF phase for measurement of T2* simultaneously with δf, T1, and T2. Magn. Reson. Med. 81, 1849–1862 (2019).
5. Liao, C. et al. 3D MR fingerprinting with accelerated stack-of-spirals and hybrid sliding-window and GRAPPA reconstruction. Neuroimage 162, 13–22 (2017).
6. Ma, D. et al. Fast 3D magnetic resonance fingerprinting for a whole-brain coverage. Magn. Reson. Med. 79, 2190–2197 (2018).
7. Gómez, P. A. et al. Rapid three-dimensional multiparametric MRI with quantitative transient-state imaging. Scientific Reports vol. 10 (2020).
8. Cao, X. et al. Fast 3D brain MR fingerprinting based on multi-axis spiral projection trajectory. Magn. Reson. Med. 82, 289–301 (2019).
9. Cao, X. et al. Optimized multi-axis spiral projection MRF with subspace reconstruction for rapid 1-mm isotropic whole-brain MRF in 2 minutes. Proc Intl Soc Mag Reson Med 29, 0173 (2021).
10. Zhao, B. et al. Improved magnetic resonance fingerprinting reconstruction with low-rank and subspace modeling. Magn. Reson. Med. 79, 933–942 (2018).
11. Gao, Y. et al. Multishot diffusion-prepared magnitude-stabilized balanced steady-state free precession sequence for distortion-free diffusion imaging. Magn. Reson. Med. 81, 2374–2384 (2019).
12. Gao, Y. et al. 3D isotropic resolution diffusion-prepared magnitude-stabilized bSSFP imaging with high geometric fidelity at 1.5 Tesla. Med. Phys. 47, 3511–3519 (2020).
13. Lu, L. et al. Diffusion-prepared fast imaging with steady-state free precession (DP-FISP): A rapid diffusion MRI technique at 7 T. Magn. Reson. Med. 68, 868–873 (2012).
14. Lu, L. et al. Diffusion-prepared fast imaging with steady-state free precession (DP-FISP): A rapid diffusion MRI technique at 7 T. Magn. Reson. Med. 68, 868–873 (2012).
15. Weigel, M. Extended phase graphs: Dephasing, RF pulses, and echoes - Pure and simple. J. Magn. Reson. Imaging 41, 266–295 (2015).
16. Tamir, J. I. et al. T2 shuffling: Sharp, multicontrast, volumetric fast spin-echo imaging. Magn. Reson. Med. 77, 180–195 (2017).
17. Zhang, T., Pauly, J. M. & Levesque, I. R. Accelerating parameter mapping with a locally low rank constraint. Magn. Reson. Med. 73, 655–661 (2015).
18. Uecker, M., Tamir, J. I., Ong, F. & Lustig, M. The BART Toolbox for Computational Magnetic Resonance Imaging. Ismrm (2016).
19. Terem, I. et al. 3D amplified MRI (aMRI). Magn. Reson. Med. 86, 1674–1686 (2021).
20. Yang, G. & McNab, J. A. Eddy current nulled constrained optimization of isotropic diffusion encoding gradient waveforms. Magn. Reson. Med. 81, 1818–1832 (2019).
Figures