Introduction

Eddy current offset correction is an essential step in preprocessing 4D flow data for accurate flow quantification. Differing offset errors in each velocity encoding direction induce disparate spatiotemporal inaccuracies in the 4D flow velocity vector-field components. Limitations of available eddy current correction methods include 1) manual methods can be time-consuming and observer-dependent; 2) automated methods (e.g., deep learning) may require large training data and have limited generalizability to different scan protocols; 3) independent optimization of each velocity component and time step does not fully account for complex spatiotemporal errors 4) sensitivity to FOV wraparound errors. To address these limitations, we propose a semi-automated self-calibrating method (no training data) to simultaneously optimize eddy current corrections and detect wraparound errors. The proposed method uses a recently developed 4D flow-field disparity signature technique^1,2 as a spatiotemporal vector-field optimization metric. The signature technique stochastically encodes the profile of pairwise vector disparity of the entire 3-directional velocity field. We hypothesize that disparate spatiotemporal eddy current errors over the velocity directions result in altered flow-field disparity signatures that would further diverge in case of wraparound errors. In this study, we aimed to show the method’s feasibility and generalizability to two different 4D flow protocols (CS and GRAPPA).

Methods

Our IRB-approved study included 98 subjects: 64 atrial fibrillation patients scanned using a PEAK-GRAPPA 4D flow protocol in a sagittal orientation (Non-CS) and 34 healthy volunteers scanned using a compressed sensing (CS) 4D flow protocol in a coronal orientation (Table 1).

Eddy current correction: Static tissue regions over all the slices were defined as voxels with temporal standard deviation below a static tissue threshold ($$$\tau$$$). A 3D linear regression correction was applied according to [3].

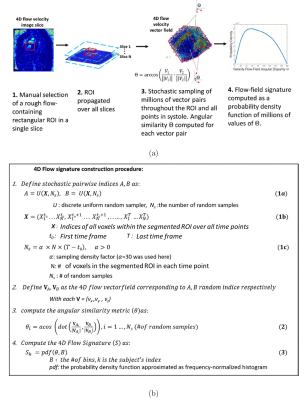
Optimization of eddy current correction using 4D flow-field disparity signature technique: A rough 2D ROI containing flow was manually selected and propagated over all slices and time frames (Fig. 1). The 4D flow-field disparity signature was computed as a probability density function of ~30 million pairwise angular disparities (Θ) over the spatiotemporal ROI^1,2 (Fig. 1). The eddy current correction and resulting signature were iteratively computed with increasing $$$\tau$$$ with step size of 0.001. Root mean square error (RMSE) was computed between successive signatures. Criteria for signature convergence to optimal threshold $$$\tau_{auto}$$$ were RMSE<1% for 10 successive iterations.

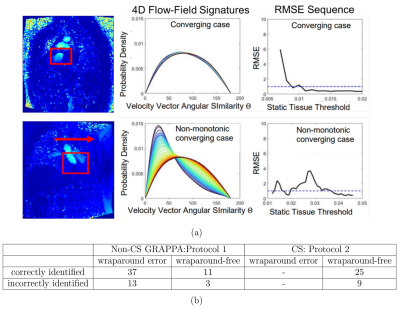
Wraparound error detection: Presence of wraparound artifact was defined as non-monotonic sequence of RMSE between signatures prior to $$$\tau_{auto}$$$. Linear change point analysis⁴ was applied to the RMSE sequence. Non-monotonicity criteria were defined by the presence of a segment with a positive slope or an increase in RMSE over 3 iterations (Fig. 2a).

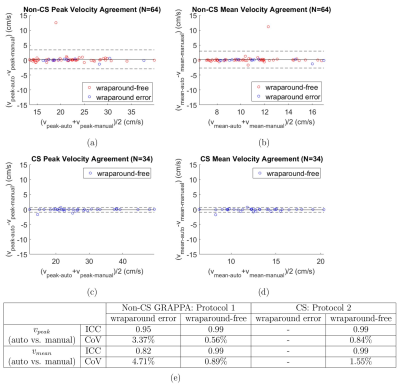
Validation: Ground-truth for wraparound errors was determined manually by a blinded visual inspection of 4D flow magnitude slices. 4D Flow Images were processed using and a manually optimized threshold $$$\tau_{manual}$$$. Manual corrections were computed within FOV bounds that exclude regions with wraparound errors from static tissue. In automated cases with successful wraparound error detection, the computation was similarly bounded. One iteration of velocity anti-aliasing was performed. Left atrial (LA) Peak ($$$v_{peak-auto}$$$, $$$v_{peak-manual}$$$) and mean ($$$v_{mean-auto}$$$, $$$v_{mean-manual}$$$) velocities were computed over the cardiac cycle and compared using Bland-Altman, coefficient of variation (CoV), intraclass correlation (ICC).

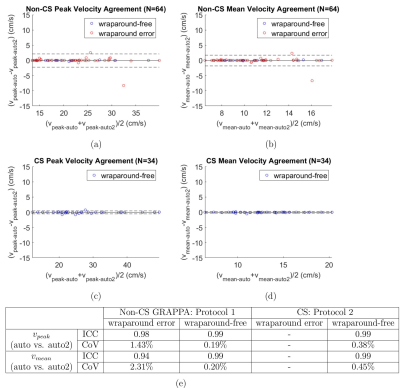
Intra-observer variability: To assess sensitivity of the algorithm to the only manual input (choice of ROI, Fig. 1 step 2), the analysis of all cases was repeated using a newly defined ROI resulting in a new automated threshold $$$\tau_{auto2}$$$. $$$v_{peak-auto}$$$ vs. $$$v_{peak-auto2}$$$ and $$$v_{mean-auto}$$$ vs. $$$v_{mean-auto2}$$$ agreement was tested between data corrected using $$$\tau_{auto}$$$ versus $$$\tau_{auto2}$$$.

Results

Wraparound error detection in the 34 CS cases, all of which were wraparound-free, had an accuracy of 73.5%. Of the 64 Non-CS cases, accuracy was 75%, sensitivity was 74% and specificity was 78.6% (Fig. 2b).

As summarized in Figure 3, there was excellent agreement between $$$v_{peak-auto}$$$ and $$$v_{peak-manual}$$$ in wraparound error and wraparound-free Non-CS cases and in wraparound-free CS cases. There was similarly excellent agreement between($$$v_{mean-auto}$$$ and $$$v_{mean-manual}$$$.

Intra-observer variability analysis of manual ROI selection, summarized in Figure 4, showed excellent agreement between $$$v_{peak-auto}$$$ and $$$v_{peak-auto2}$$$ in both protocols, in cases with or without wraparound error. There was similarly excellent agreement between $$$v_{mean-auto}$$$ and $$$v_{mean-auto2}$$$.

Discussion and Conclusions

Using a recently introduced 4D flow-field disparity signature to encode the entire spatiotemporal three-directional velocity vector-field, we developed a self-calibrating method for optimizing eddy current corrections and simultaneously identifying wraparound errors. The results demonstrated generalizability of the method, showing excellent agreement in LA peak and mean velocity vs. the manually optimized, in two 4D Flow MRI protocols (CS, GRAPPA) with different scan parameters as well as in the cases with identified wraparound artifact. We found high LA velocity agreement in most undetected wraparound cases, suggesting that smaller wraparound region errors may have had minimal impact on the eddy current correction in these cases. In one error case with severe deviation, the error was undetected, and the image may be uncorrectable. LA velocity showed excellent agreement between values of the only manual input (ROI selection). Future work will focus on automated adjustment of the wraparound error region, as well as expanding to different eddy current correction schemes and 4D flow scan protocols.

Acknowledgements

This research is supported in part by the Transformational Project Award AHA 20TPA35490311 from the American Heart Association (AHA).