Introduction and Motivation

Iterative Neural Networks (INNs) nowadays define the state-of-the-art for image reconstruction problems across all imaging modalities. Their success can be attributed to the fact that the physical model of the considered inverse problem is used in the network architecture. Using INNs, one can learn regularizers which are tailored to the considered forward model and to the employed reconstruction algorithm the network implicitly defines.
Because NNs are still black-boxes from a theoretical point of view, the reason for the superiority of one specific INN compared to others is often unclear. Training with the physical model reduces the maximum-error bound [1], stabilizes the training process [2] and reduces the amount of required training data [3]. Thus, it is distinctly harder to overfit INNs compared to model-agnostic NNs and, to some extent, one can in principle always obtain "better" reconstruction networks by only increasing the number of trainable parameters (NTP) as long as no overfitting is observed. We believe that this aspect - if not taken into consideration - can possibly hinder the development of genuinely novel reconstruction methods because the success of specific methods might mistakenly be attributed to the network-capacity rather than the methods itself.
Here, we consider three INNs-based approaches and demonstrate that by comparing them without indicating NTP, wrong conclusions could be drawn.

Methods

We consider an accelerated 2D radial MR image reconstruction problem
$$\mathbf{A} \mathbf{x} + \mathbf{e} = \mathbf{y},$$
where $$$\mathbf{A}$$$ denotes the encoding operator, $$$\mathbf{x}$$$ the MR image, $$$\mathbf{e}$$$ random Gaussian noise and $$$\mathbf{y}$$$ the undersampled $$$k$$$-space data. In non-Cartesian acquistions, pre-conditioning is often used by weighting the $$$k$$$-space data with a diagonal density-compensation operator $$$\mathbf{W}$$$. The data-discrepancy term and the respective gradient are given by
$$
D_{\mathbf{W}}(\mathbf{A}\mathbf{x},\mathbf{y}) := \frac{1}{2}\|\mathbf{W}^{1/2} (\mathbf{A}\mathbf{x}-\mathbf{y})\|_2^2,\\
\nabla_{\mathbf{x}} D_{\mathbf{W}}(\mathbf{A}\mathbf{x},\mathbf{y}) = \mathbf{A}^{\sharp}(\mathbf{A}\mathbf{x}-\mathbf{y}),
$$
with $$$\mathbf{A}^{\sharp}:=\mathbf{A}^H \mathbf{W}^{1/2}$$$.
We consider three different INNs-based methods based on a learned CNN-projected gradient descent (CNN-Proj) [4], on learned regularizers using a Landweber iteration (CNN-LW) and on a fixed-point iteration using the MoDL-architecture (MoDL) [5]. Note that all three methods can be derived from an underlying functional which defines the reconstruction problem.
Given $$$\mathbf{x}_0:=\mathbf{A}^{\sharp} \mathbf{y}$$$ and an appropriate CNN-architecture $$$f_{\Theta}$$$, for $$$0\leq k\leq T$$$, the methods are given by
$$
\mathbf{z}_k = \mathbf{x}_k - \lambda \, \mathbf{A}^{\sharp}(\mathbf{A}\mathbf{x}-\mathbf{y}), \\ \mathbf{x}_{k+1} = f_{\Theta}(\mathbf{z}_k) \tag{CNN-Proj},
$$
$$
\mathbf{x}_{k+1} = \mathbf{x}_k - \lambda \, f_{\Theta}(\mathbf{x}_{k}) - \lambda \, \mathbf{A}^{\sharp}(\mathbf{A}\mathbf{x}-\mathbf{y}), \tag{CNN-LW}
$$
and
$$
\mathbf{z}_k = f_{\Theta}(\mathbf{x}_k), \\
\mathbf{x}_{k+1} = \underset{\mathbf{x}}{\arg \min} \, \frac{1}{2} \|\mathbf{W}^{1/2} (\mathbf{A}\mathbf{x}-\mathbf{y})\|_2^2 + \frac{\lambda}{2} \, \|\mathbf{x} - \mathbf{z}_k\|_2^2, \tag{MoDL}
$$
where $$$\lambda>0$$$ for MoDL and $$$ 0 < \lambda <2/ \|\mathbf{A}\|^2$$$ for CNN-LW and CNN-Proj. For the three methods, $$$f_{\Theta}$$$ allows for a different interpretation. In CNN-Proj, we can identify $$$f_{\Theta}$$$ to perform a learned projection. In CNN-LW, $$$f_{\Theta}$$$ corresponds to the gradient of a regularizer parametrized by $$$\Theta$$$ and in MoDL, $$$f_{\Theta}$$$ yields a CNN-based image-prior.
Further, note that CNN-Proj and CNN-LW consist of the exact same components, namely the gradient $$$ \nabla_{\mathbf{x}} D_{\mathbf{W}} $$$ and $$$f_{\Theta}$$$. However, CNN-LW is by design more data-consistent compared to CNN-Proj because the last operation is not given by the application of the CNN. Further, MoDL is more data-consistent than CNN-LW, because instead of applying the gradient $$$\nabla_{\mathbf{x}} D_{\mathbf{W}}$$$, it solves a quadratic problem with respect to $$$\mathbf{x}$$$.
By construction, we would therefore expect MoDL to surpass both CNN-LW and CNN-Proj and CNN-LW to surpass CNN-Proj in terms of performance.

For $$$f_{\Theta}$$$, we used a 2D U-Net [6] which we parametrized by $$$E,C$$$ and $$$K$$$, denoting the number of encoding stages, the number of convolutional layers per stage and the initial number of filters, respectively. We trained the three methods with $$$T=6$$$ for different combinations of $$$E=1,...,5 $$$ with $$$C=2$$$ and $$$K=16$$$, yielding different NTPs.
As dataset, we used 2000 images from the MRI dataset in [7], which we split into 1400/400/200 images for training, validation and testing, respectively. The initial reconstructions were retrospectively simulated using an acceleration factor of $$$R\approx 18$$$ with $$$N_c=12$$$ coils. All networks were trained for 500 epochs with ADAM with a learning rate of $$$10^{-4}$$$ using the $$$L_2$$$-error as a loss function.

Results

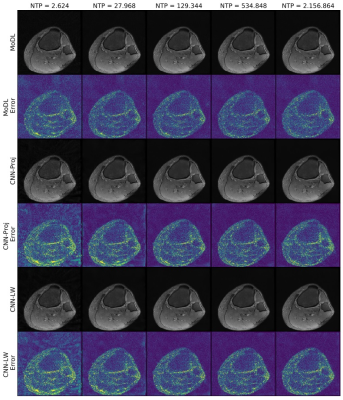
In Figure 1, we see the training- and validation-errors for the different network architectures we trained on. The superiority of MoDL for this type of imaging problem is clearly visible compared to CNN-LW and CNN-Proj. Note that this observation holds for all different NTP. However, it is also possible to surpass MoDL with CNN-LW and CNN-Proj if NTP is high enough. The box-plots in Figure 2 and the images in Figure 3 highlight the described phenomenon well.

Discussion and Conclusion

Although MoDL consistently outperforms CNN-Proj and CNN-LW at equal network-capacity, increasing NTP makes it possible to surpass MoDL both with CNN-Proj and CNN-LW.
This simple example shows that comparing different INNs without indicating the NTP can indeed yield to a misinterpretation of the performance of the methods. Further, using larger GPUs, one can typically also increase NTPs which also possibly introduces a hardware-bias.
We therefore encourage researchers to always report NTP in their methods and to be aware of the possibility of this issue. Further, we think that NTP could and should be used as a standard metric for evaluating machine learning-based methods for image reconstruction.

Acknowledgements

No acknowledgement found.