INTRODUCTION

Recently, deep learning methods using neural networks have been investigated to reconstruct undersampled k-space data through learning multilevel image representation to remove image artifacts and noises. However, while those methods focus on developing novel reconstruction networks or improving network training strategies, very few studies have investigated the optimization of k-space acquisition for learning-based reconstruction. The k-space undersampling patterns are usually kept the same as those previously used in parallel imaging and compressed sensing. This study will investigate accelerating MRI by learning k-space sampling to maximize image acquisition efficiency for deep learning-based image reconstruction. The k-space acquisition is formulated as a dynamic optimization process and is solved using a neural Ordinary Differential Equation (ODE)[1]. This ODE system is first initialized, and the trajectories are then dynamically adjusted towards an optimal pattern that provides the best acquisition efficiency. A joint training strategy to optimize both the neural ODE system and a deep learning reconstruction model is implemented, providing optimal data acquisition and image reconstruction.

METHODS

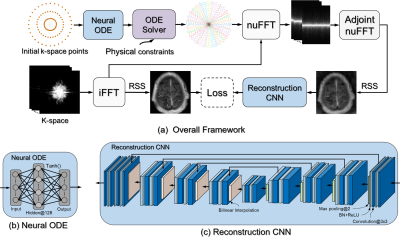
(1) Neural ODE: ODE mathematically describes variable changes using integrals and derivatives to model a dynamic system. Neural ODE uses a neural network to parameterize the dynamics of the variable[1]. Neural ODE has recently shown impressive performance in sequential data optimization for regular and irregular time sampling[2], making it an ideal new approach for optimizing MRI k-space trajectory. Figure 1 shows the fundamental theory of using neural ODE for k-space optimization.
(2) Network Implementation: As illustrated in Figure 2, the proposed algorithm consists of two deep learning networks with their associated data processing pathways. First, a neural ODE is introduced to approximate the dynamic evolution of the k-space trajectory from its initial status (Cartesian or non-Cartesian). Second, the optimized trajectory from neural ODE will be used as the input for a second deep learning reconstruction network, trained to remove image artifacts and noise in the reconstructed images against the reference fully sampled images. These two networks are jointly trained to ensure mutual convergence through competitive learning. Furthermore, our ODE system incorporates the MRI hardware constraints (maximum imaging gradient and slew-rate) to create physically feasible acquisition trajectories.
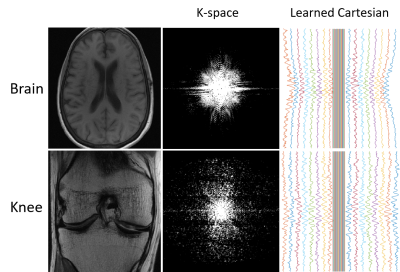
(3) Method Evaluation: To demonstrate the capability of our method for optimizing various trajectories, we investigated initializing the trajectory optimization using three different k-space sampling patterns, including Cartesian, radial, and spiral, respectively. Acceleration was implemented using a reduced number of shots (e.g., lines, spokes, or interleaves), including N= 4, 8, 16, and 32, respectively. Experiments were conducted using the image datasets from fastMRI database[3], which contains knee and brain MR images acquired with different MR sequences. For the knee images, 80 subjects were randomly selected for training (N=60), validation (N=5), and testing (N=15). The fully-sampled knee image dataset was acquired using a 2D coronal proton density-weighted fast spin-echo sequence with the routine knee MRI protocol. For the brain images, 65 subjects were randomly selected for training (N=50), validation (N=5), and testing (N=10). The brain datasets include fully-sampled 2D axial T1-weighted images without (AXT1) and with (AXT1POST) the contrast agent administration. All images were unified into a 256x256 matrix size via cropping the central region of images that were obtained by taking the inverse Fourier Transform of the fully sampled k-space data. The network training was implemented using a step-wise strategy to jointly optimize the trajectory and image reconstruction networks at a total of 100 epochs with Adam optimizer[4].

RESULTS

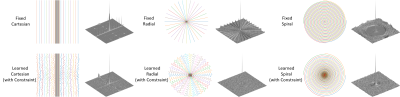
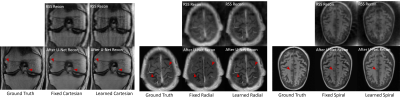
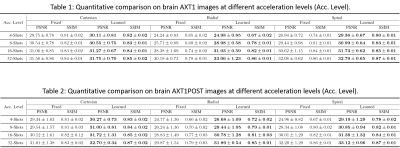
The learned k-space trajectories are demonstrated in Figure 3. The learned trajectories tend to densely sample the central k-space region where the information density is higher than other regions. The learned trajectories are divergent at the peripheral k-space region since the trajectories prefer to acquire appropriate high-frequency components, which are typically sparse in the k-space. Compared with the fixed point-spread function (PSF), the learned trajectory can lead to a PSF with reduced side lobes and more homogeneous sampling of the neighboring pixels. This can result in reduced structural and aliasing imaging artifacts in the undersampled images. The reconstructed images from the learned trajectories are demonstrated in Figure 4. These images were compared with the images directly reconstructed using fixed trajectory. As shown, the reconstructed images from learned trajectories are consistently better than those from the fixed trajectories for each type. The group-wise quantitative analyses further confirmed the qualitative comparisons. Tables 1 and 2 summarized the quantitative comparison between images reconstructed using the fixed and learned trajectories in all testing AXT1 and AXT1POST brain image datasets at different acceleration levels. The learned trajectories generally show significantly better reconstruction quality (p<0.05) than the fixed ones in terms of PSNR and SSIM metrics.

DISCUSSION AND CONCLUSION

This study demonstrated the feasibility of optimizing MRI k-space acquisition using a deep learning framework consisting of a neural ODE and an image reconstruction network. The proposed method was evaluated under Cartesian and Non-Cartesian trajectories to demonstrate the generalization of the method. We have shown that the proposed method consistently outperforms the regular fixed k-space sampling strategy. The optimization is efficient and adaptable for various trajectories at different image sequences, contrast, and anatomies. The proposed method provides a new opportunity for improving rapid MRI, ensuring optimal acquisition while maintaining high-quality image reconstruction.

Acknowledgements

No acknowledgement found.