0049

Deep-learning-based raw data generation for deep-learning-based image reconstruction

Frank Zijlstra^1,2 and Peter T. While^1,2
¹Department of Radiology and Nuclear Medicine, St. Olav's University Hospital, Trondheim, Norway, ²Department of Circulation and Medical Imaging, NTNU - Norwegian University of Science and Technology, Trondheim, Norway

Synopsis

This study demonstrates the potential of using deep learning for generating raw data to augment raw datasets of limited size for use in deep-learning-based MR image reconstruction. Using an adversarial autoencoder architecture, variability in 10 T1-weighted raw datasets from the fastMRI database was learned and recombined into new, random raw data. We trained a deep-learning-based Compressed Sensing reconstruction using both conventional approaches with real raw data and compared the results to training with generated raw data. The reconstruction from generated raw data showed improved reconstruction results and better generalization to scans with slightly different echo times.

Introduction

Deep-learning-based MR image reconstruction has shown great promise for accelerated imaging^1,2. However, training these systems is inherently limited by the availability of raw data, which limits its application to new sequences.

The recent release of the fastMRI dataset^3,4 with 8400 raw datasets has enabled training of complex reconstruction models that rely on “big” data. However, in most research environments, gaining access to hundreds of raw datasets is virtually impossible. While hospital databases contain a wealth of information in terms of reconstructed, magnitude-only images, raw data is almost never stored. Furthermore, in the development of new imaging sequences magnitude images may not even be available.

Although magnitude-only data is sometimes used for training reconstruction models, this can lead to serious mismatches between the training data and actually acquired raw data⁵. Furthermore, model-based generation of missing phase and coil sensitivity information is often based on simplified models (e.g. polynomials).

In conventional deep learning, when limited training data is available, data augmentation (e.g. rotation/translation) can be applied to enhance the size and quality of training datasets⁶. Here, we investigate using deep learning to generate synthetic raw data to further enhance the size of raw data datasets for deep-learning-based image reconstruction. We trained neural networks to generate raw data from a limited number of raw datasets from the fastMRI database, and validated the generated raw data in a deep-learning-based compressed sensing reconstruction.

Methods

Data
From the NYU fastMRI database we selected 50 (40 train, 10 test) T1-weighted FLASH datasets acquired at 3 tesla (TE=3.4, TR=250, TI=300, matrix=16x320x320). The datasets were coil-compressed to 8 virtual receive coils⁷ to provide consistent data dimensions to the neural networks, and coil sensitivity maps (CSMs) were calculated⁸. To investigate generalization, we also constructed a dataset of 50 similar T1-weighted pre-contrast images (TE=2.4ms).

Raw data generation
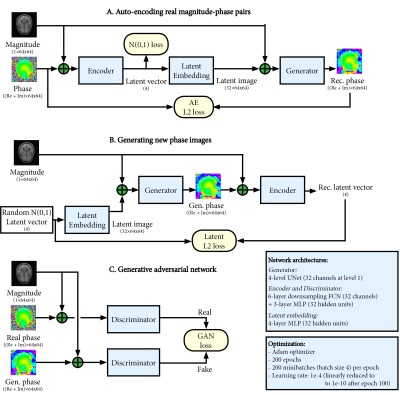
We based the raw data generation on decomposition of raw data into magnitude, phase, and CSMs. By generating phase and CSM from magnitude images, new raw data can be recombined as: $$raw_{gen}=M \cdot P_{gen} \cdot CSM_{gen}$$ The generative networks were based on a conditional adversarial auto-encoder architecture⁹ as depicted in Figure 1 (for phase maps, identically for CSMs). Importantly, this architecture can learn variability in the raw data and generate new samples through sampling a random latent vector.

The networks were trained separately for phase and CSM generation, using 10 raw datasets for training, downsampled to 64x64 for efficiency. Conventional data augmentation (rotation -20 to 20 degrees, translation -20 to 20 pixels, scale 0.8 to 1.2) was applied during training to increase variability.

Image reconstruction
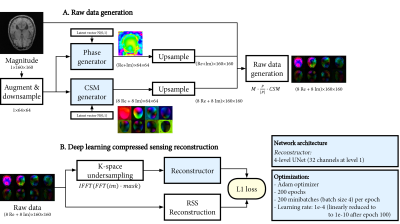
To demonstrate the raw data generation in a practical deep-learning-based compressed sensing reconstruction, we trained a 2D UNet¹⁰ reconstruction network to reconstruct magnitude images from 8 undersampled, complex-valued virtual coil images, depicted in Figure 2. For efficiency, the original data was downsampled to 160x160. A 2D 4-fold variable-density poisson-disc k-space undersampling pattern was used.

As a baseline, the network was trained with 10, 20, 30 and 40 raw datasets with TE matching to the test set. In a small data regime with only 10 datasets (single TE), we trained using conventional data augmentation on both actual raw data and generated raw data. Reconstructions were evaluated on both test sets (two different TEs) based on masked MAE and MSE metrics.

Results

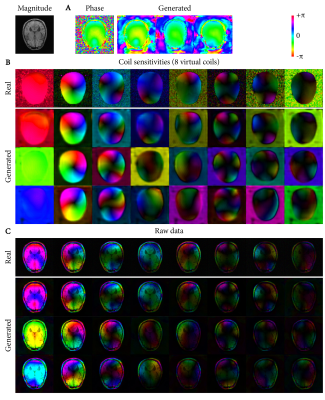
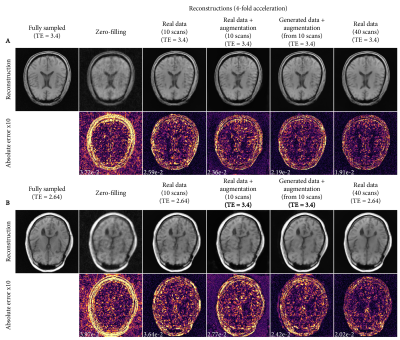
Figure 3 shows real and generated phase, CSM and raw data. The generated samples show a good representation of the variability of the dataset, but simultaneously can also match closely to real raw data.

Reconstructions from the different training strategies are shown in Figure 4, showing reduced errors when training the reconstruction network with generated raw data. Interestingly, both data augmentation and data generation show less smoothing than the baseline reconstructions.

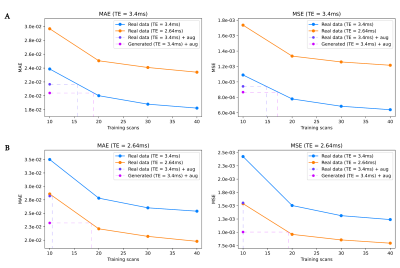
Mean reconstruction errors are shown in Figure 5. Both data augmentation and data generation using 10 scans show improved errors relative to the 10-scan baseline, achieving errors corresponding to ~50% more data for augmentation and ~80% more data for data generation (Fig 5A). Furthermore, compared to data augmentation, data generation shows improved generalization to a different echo time that was not seen during training (Fig 5B).

Discussion & Conclusion

We demonstrated that variability in raw datasets of limited size can be learned with deep learning and used to randomly generate realistic new phase and coil sensitivity maps. When these maps were recombined into synthetic raw data, deep-learning-based reconstruction benefited from the increased variability in the training data, improving reconstruction errors and generalizability over conventional data augmentation. Raw data generation may open the possibility of augmenting existing magnitude-only datasets into realistic synthetic raw data, allowing it to be included as training data for deep-learning-based reconstruction.

Both the raw data generation and reconstruction tasks presented here were performed at limited resolution, trained on only a single scan type, and trained with non-optimized network architectures, which could be improved upon in future experiments.

The presented raw data generation architecture shows that including the underlying MR physics in deep-learning experiments can provide new avenues for alleviating the raw data requirements of deep-learning-based reconstruction. Particularly when raw data is scarce this could make these reconstruction methods easier to apply to both new and existing imaging sequences.

Acknowledgements

This work was supported by the Research Council of Norway (FRIPRO Researcher Project 302624).

References

1. Knoll F, Murrell T, Sriram A, et al. Advancing machine learning for MR image reconstruction with an open competition: Overview of the 2019 fastMRI challenge. Magn. Reson. Med. 2020;84:3054–3070

2. Zhu B, Liu JZ, Cauley SF, Rosen BR, Rosen MS. Image reconstruction by domain-transform manifold learning. Nature 2018;555:487–492

3. Zbontar J, Knoll F, Sriram A, et al. fastMRI: An Open Dataset and Benchmarks for Accelerated MRI. ArXiv:1811.08839 [physics, stat]; 2019.

4. Knoll F, Zbontar J, Sriram A, et al. fastMRI: A Publicly Available Raw k-Space and DICOM Dataset of Knee Images for Accelerated MR Image Reconstruction Using Machine Learning. Radiol. Artif. Intell. 2020;2:e190007

5. Shimron E, Tamir JI, Wang K, Lustig M. Subtle Inverse Crimes: Naïvely training machine learning algorithms could lead to overly-optimistic results. ArXiv:2109.08237 [cs]; 2021.

6. Shorten C, Khoshgoftaar TM. A survey on Image Data Augmentation for Deep Learning. J. Big Data 2019;6:60

7. Zhang T, Pauly JM, Vasanawala SS, Lustig M. Coil compression for accelerated imaging with Cartesian sampling. Magn. Reson. Med. 2013;69:571–582

8. Inati SJ, Hansen MS, Kellman P. A Fast Optimal Method for Coil Sensitivity Estimation and Adaptive Coil Combination for Complex Images. In: Proceedings of the 22nd Annual Meeting of the ISMRM, 2014.

9. Makhzani A, Shlens J, Jaitly N, Goodfellow I, Frey B. Adversarial Autoencoders. ArXiv:1511.05644 [cs]; 2016.

10. Ronneberger O, Fischer P, Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In: Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015. Lecture Notes in Computer Science. Springer, Cham; 2015. pp. 234–241

Figures

Figure 1. Conditional adversarial auto-encoder architecture for phase map generation. A. Real magnitude-phase pairs are auto-encoded into a normally-distributed latent vector, which must generate back into the real phase map. B. A phase map generated from a random latent vector must encode back into the same latent vector. C. A cGAN architecture trains generated phase maps to be indistinguishable from real phase maps. Networks were chosen as UNet, fully convolutional networks (FCNs) and multi-layer perceptrons (MLPs). Training time was 4.5h on an RTX 2080 Super GPU.

Figure 2. A. Raw data generation using the phase and CSM generation networks. B. Deep-learning Compressed Sensing reconstruction of 2D image-space raw data (either real or generated) consisting of 8 virtual coils. A root-sum-of-squares reconstruction from fully sampled raw data was used as the target reconstruction. The undersampling mask was a 2D 4-fold variable-density random poisson-disc pattern. Training time was ~20min on an RTX 2080 Super GPU.

Figure 3. Phase (A), coil sensitivities (B) and raw data (C) generated from a single magnitude image. Three curated randomly generated phase, coil sensitivty and raw data samples are shown, with the first sample chosen as one nearly identical to the real raw data corresponding to the magnitude image. Complex images are represented with magnitude as image intensity and phase as image colour.

Figure 4. Compressed sensing reconstructions and absolute error maps (x10) for a single image from the TE=3.4 (A) and TE=2.64 (B) test sets. Reconstructions are shown for deep learning reconstruction networks trained with 10 (3rd column) and 40 (7th column) raw datasets with TE matching the test data; as well as trained on 10 scans of TE=3.4 data, with data augmentation (4th column) and raw data generation and data augmentation (5th column). Fully-sampled and zero-filled reconstruction are shown for reference. Error maps are annotated with the masked MAE value of the entire 3D image.

Figure 5. Mean absolute (MAE, left column) and mean squared (MSE, right column) reconstruction errors over the entire TE=3.4 (A) and TE=2.64 (B) test sets. Errors are shown for deep learning reconstruction networks trained with 10 to 40 raw datasets on TE=3.4 (blue) and TE=2.64 data (orange); as well as trained on 10 scans of TE=3.4 data, with data augmentation (purple) and raw data generation and data augmentation (pink), with dashed lines to visualize the effective amount of training data that would be required to achieve the same error level without data augmentation/generation.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

0049

DOI: https://doi.org/10.58530/2022/0049