0017

Tensor-valued Encoding in the Human Heart In vivo
Irvin Teh1, David Shelley2, Ana-Maria Poenar1, Erica Dall'Armellina1, Sven Plein1, Jürgen E. Schneider1, and Filip Szczepankiewicz3
1Leeds Institute of Cardiovascular and Metabolic Medicine, University of Leeds, Leeds, United Kingdom, 2Leeds Teaching Hospitals Trust, Leeds, United Kingdom, 3Clinical Sciences, Lund University, Lund, Sweden

Synopsis

Tensor-valued encoding holds great promise in enhancing specificity in myocardial characterisation relative to diffusion tensor imaging (DTI). However, its application in the heart is challenging due to motion and limited SNR. In this work, we employed optimized diffusion encoding waveforms with up to 2nd order motion compensation and compensation for concomitant gradient effects to demonstrate the first in vivo application of q-space trajectory imaging (QTI) in the human heart. Baseline myocardial measurements of microscopic fractional anisotropy, as well as isotropic and anisotropic mean kurtosis are reported for the first time in the heart.

Purpose

Cardiac diffusion MRI is an emerging method for non-invasive myocardial characterisation without use of contrast agents. Although diffusion tensor imaging (DTI) is regularly applied in disease, e.g. hypertrophic1, 2 and dilated cardiomyopathy3, infarction4 and amyloidosis5, it has poor specificity. Measuring the effects of microscopic anisotropy and multi-Gaussian diffusion, offers the potential for greater specificity.
Techniques applied in the preclinical ex vivo setting include double diffusion encoding (DDE) for measuring microscopic FA (µFA) which is insensitive to orientation dispersion6, oscillating gradient spin echo7, non-Gaussian signal models8, compartmental models9, time dependent diffusion10, 11 and tensor-valued encoding12.

Tensor-valued encoding, in particular, can be a highly efficient13 method for probing µFA and effects of multi-Gaussian diffusion, and has found application in various organs in brain and body imaging13-15. By employing arbitrary gradient waveforms, b-tensors of arbitrary shape can be efficiently produced, e.g. linear, planar and spherical b-tensor encoding (LTE, PTE, STE). By combining multiple b-tensor shapes, we can etimate microscopic diffusion anisotropy (µFA) as well as isotropic, anisotropic and total mean kurtosis (MKi, MKa, MKt)16-18.

However, tensor-valued encoding in the heart is challenging due to cardiac and respiratory motion, short T2, and lower efficiency of PTE and STE waveforms compared to LTE. Previously, we demonstrated that it was possible to perform LTE, PTE and STE at relatively low b-values in heart in vivo19, 20. In this work, we demonstrate, for the first time, q-space trajectory imaging (QTI) based on tensor-valued encoding at high b-values in a healthy human volunteer.

Methods

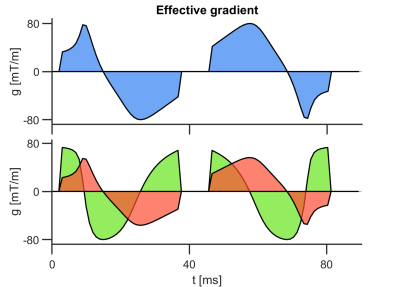
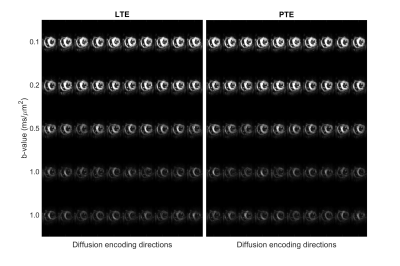
Data were acquired in two healthy volunteers on a Prisma 3T MRI scanner (Siemens Healthineers, Erlangen, Germany). Volunteers provided written consent, and the study was performed under approved ethics. Diffusion MRI data were acquired with a prototype single-shot spin-echo sequence with EPI-readout and Zoom-IT for reduced FOV imaging21. The scan was cardiac-triggered, and the subject was scanned free-breathing. Parameters were TR = 5 RR-intervals, TE = 103 ms, resolution = 3×3×10 mm3 in 5 slices, field-of-view = 320×111 mm2, b-values = [0.1, 0.2, 0.5, 1.0] ms/µm2 along [10, 10, 10, 20] rotations, repetitions = 4, total acquisition time ~40 min. LTE and PTE data were acquired alternately with randomized b-values. Gradient waveforms were motion-compensated to 2nd-order (velocity and acceleration; Figure 1)20. Data were denoised22, had Gibbs ringing removed23 in MRtrix24, and were motion/eddy-current corrected25. Parameters were estimated by q-space trajectory imaging (QTI)18 with positivity constraints on the covariance tensor26. Parameter maps are reported in one mid-myocardial short-axis slice in the left ventricle.

Results

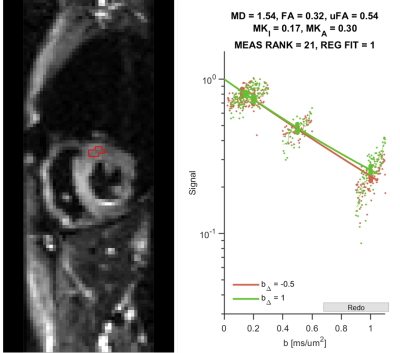
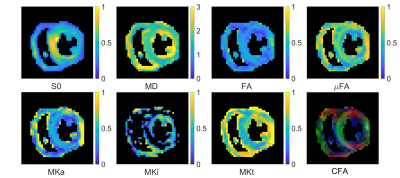
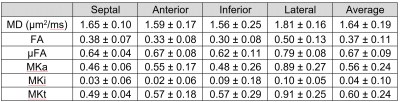
The registered images show visible diffusion contrast and minimal signal dropout (Figure 2). Plotting the log signal attenuation against b-value shows a small but measurable deviation between LTE and PTE signal at high b-value that provides the basis for estimating MKa (Figure 3). Parameter maps (Figure 4), and QTI parameters are reported in the septal, anterior, inferior and lateral walls of one healthy volunteer (Table 1).

Discussion and Conclusions

We report the first measurements of µFA and MK in the human heart in vivo. We observe that µFA > FA which indicates the presence of intra-voxel orientation dispersion, which would be consistent with the known transmural variation in cardiomyocyte orientation. Both µFA and MK were lower in the myocardium compared to in brain white matter where they have been reported as 0.74 and 0.93 respectively18. This may reflect the larger cell diameter and higher permeability of cardiomyocytes compared to axons. Low MKi values reflect low intra-voxel variation in isotropic diffusivity, which may reflect the low microstructural heterogeneity in healthy myocardium. As diffusion time effects have been observed at similar diffusion times, it is reasonable to assume that they are present in the QTI data as well. To minimise potential bias, we implemented a version of PTE that shares the frequency content of LTE along one axis.

Tensor-valued encoding in the heart in vivo is challenging for several reasons. First, is the need to compensate for motion. Constraining the motion-encoding reduces the encoding efficiency, and extends the required encoding time27. Coupled with a relatively short T2 (compared to brain), the SNR is relatively low. These issues were addressed by tailoring acceleration-nulled PTE gradient waveforms that had an efficient LTE sub-set20, in combination with large voxels, denoising and Gibbs removal. Nevertheless, the frequency content in LTE and PTE were not matched exactly, which may cause a bias27. Finally, a larger sample size is required to establish baseline parameter values. In future work, we will refine the acquisition and post-processing pipeline for optimal spatial resolution and acquisition time and quantify potential biases in data.

In conclusion, we have demonstrated, for the first time, QTI in the human heart in vivo, opening the way for improved specificity in characterising the myocardial microstructure.

Acknowledgements

We thank Jan Morez and Ben Jeurissen for supplying the code for the constrained QTI fitting. We thank Siemens Healthcare for the pulse sequence development environment. This work was supported by the British Heart Foundation, UK (PG/19/1/34076, FS/13/71/30378, CH/16/2/32089).

References

1. Das A, Chowdhary A, Kelly C, Teh I, Stoeck CT, Kozerke S, Maxwell N, Craven TP, Jex NJ, Saunderson CED, Brown LAE, Ben-Arzi H, Sengupta A, Page SP, Swoboda PP, Greenwood JP, Schneider JE, Plein S and Dall'Armellina E. Insight Into Myocardial Microstructure of Athletes and Hypertrophic Cardiomyopathy Patients Using Diffusion Tensor Imaging. Journal of magnetic resonance imaging : JMRI. 2020.

2. Ariga R, Tunnicliffe EM, Manohar SG, Mahmod M, Raman B, Piechnik SK, Francis JM, Robson MD, Neubauer S and Watkins H. Identification of Myocardial Disarray in Patients With Hypertrophic Cardiomyopathy and Ventricular Arrhythmias. J Am Coll Cardiol. 2019;73:2493-2502.

3. Nielles-Vallespin S, Khalique Z, Ferreira PF, de Silva R, Scott AD, Kilner P, McGill LA, Giannakidis A, Gatehouse PD, Ennis D, Aliotta E, Al-Khalil M, Kellman P, Mazilu D, Balaban RS, Firmin DN, Arai AE and Pennell DJ. Assessment of Myocardial Microstructural Dynamics by In Vivo Diffusion Tensor Cardiac Magnetic Resonance. J Am Coll Cardiol. 2017;69:661-676.

4. Das A, Kelly C, Teh I, Stoeck CT, Kozerke S, Chowdhary A, Brown LAE, Saunderson CED, Craven TP, Chew PG, Jex N, Swoboda PP, Levelt E, Greenwood JP, Schneider JE, Plein S and Dall'Armellina E. Acute Microstructural Changes after ST-Segment Elevation Myocardial Infarction Assessed with Diffusion Tensor Imaging. Radiology. 2021;299:86-96.

5. Gotschy A, von Deuster C, van Gorkum RJH, Gastl M, Vintschger E, Schwotzer R, Flammer AJ, Manka R, Stoeck CT and Kozerke S. Characterizing cardiac involvement in amyloidosis using cardiovascular magnetic resonance diffusion tensor imaging. Journal of cardiovascular magnetic resonance : official journal of the Society for Cardiovascular Magnetic Resonance. 2019;21:56.

6. Teh I, Lundell H, Whittington HJ, Dyrby TB and Schneider JE. Resolving Microscopic Fractional Anisotropy in the Heart. Paper presented at: In: Proceedings of the 24th Annual Meeting of ISMRM, Singapore; 2016.

7. Teh I, Schneider JE, Whittington HJ, Dyrby TB and Lundell H. Temporal Diffusion Spectroscopy in the Heart with Oscillatiing Gradients. Proc Int Soc Magn Reson Med. 2017:3114.

8. McClymont D, Teh I, Carruth E, Omens J, McCulloch A, Whittington HJ, Kohl P, Grau V and Schneider JE. Evaluation of non-Gaussian diffusion in cardiac MRI. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2017;78:1174-1186.

9. Farzi M, McClymont D, Whittington H, Zdora MC, Khazin L, Lygate CA, Rau C, Dall'Armellina E, Teh I and Schneider JE. Assessing Myocardial Microstructure with Biophysical Models of Diffusion MRI. IEEE transactions on medical imaging. 2021;PP.

10. Lasic S, Lundell H, Szczepankiewicz F, Nilsson M, Schneider JE and Teh I. Time-dependent and anisotropic diffusion in the heart: linear and spherical tensor encoding with varying degree of motion compensation. Proc Int Soc Magn Reson Med. 2020:4300.

11. Lundell H, Lasic S, Szczepankiewicz F, Nilsson M, Topgaard D, Schneider JE and Teh I. Stay on the beat: tuning in on time-dependent diffusion in the heart. Proc Int Soc Magn Reson Med. 2020:959.

12. Teh I, Lasic S, Lundell H, Wereszczyńska B, Budde M, Dall'Armellina E, Yuldasheva N, Szczepankiewicz F and Schneider JE. Multidimensional Diffusion MRI in the Ex Vivo Mouse Heart. Proc Int Soc Magn Reson Med. 2021:3618.

13. Nilsson M, Szczepankiewicz F, Brabec J, Taylor M, Westin CF, Golby A, van Westen D and Sundgren PC. Tensor-valued diffusion MRI in under 3 minutes: an initial survey of microscopic anisotropy and tissue heterogeneity in intracranial tumors. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2020;83:608-620.

14. Nery F, Szczepankiewicz F, Kerkela L, Hall MG, Kaden E, Gordon I, Thomas DL and Clark CA. In vivo demonstration of microscopic anisotropy in the human kidney using multidimensional diffusion MRI. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2019;82:2160-2168.

15. Nilsson M, Eklund G, Szczepankiewicz F, Skorpil M, Bryskhe K, Westin CF, Lindh C, Blomqvist L and Jaderling F. Mapping prostatic microscopic anisotropy using linear and spherical b-tensor encoding: A preliminary study. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2021;86:2025-2033.

16. Lasic S, Szczepankiewicz F, Eriksson S, Nilsson M and Topgaard D. Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion MRI with magic-angle spinning of the q-vector. Frontiers in Physics. 2014.

17. Szczepankiewicz F, van Westen D, Englund E, Westin CF, Stahlberg F, Latt J, Sundgren PC and Nilsson M. The link between diffusion MRI and tumor heterogeneity: Mapping cell eccentricity and density by diffusional variance decomposition (DIVIDE). NeuroImage. 2016;142:522-532.

18. Westin CF, Knutsson H, Pasternak O, Szczepankiewicz F, Ozarslan E, van Westen D, Mattisson C, Bogren M, O'Donnell LJ, Kubicki M, Topgaard D and Nilsson M. Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. NeuroImage. 2016;135:345-62.

19. Lasic S, Szczepankiewicz F, Dall'Armellina E, Das A, Kelly C, Plein S, Schneider JE, Nilsson M and Teh I. Motion-compensated b-tensor encoding for in vivo cardiac diffusion-weighted imaging. NMR in biomedicine. 2020;33:e4213.

20. Szczepankiewicz F, Sjolund J, Dall'Armellina E, Plein S, Schneider JE, Teh I and Westin CF. Motion-compensated gradient waveforms for tensor-valued diffusion encoding by constrained numerical optimization. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2021;85:2117-2126. 21. Szczepankiewicz F, Sjolund J, Stahlberg F, Latt J and Nilsson M. Tensor-valued diffusion encoding for diffusional variance decomposition (DIVIDE): Technical feasibility in clinical MRI systems. PloS one. 2019;14:e0214238.

22. Cordero-Grande L, Christiaens D, Hutter J, Price AN and Hajnal JV. Complex diffusion-weighted image estimation via matrix recovery under general noise models. NeuroImage. 2019;200:391-404.

23. Kellner E, Dhital B, Kiselev VG and Reisert M. Gibbs-ringing artifact removal based on local subvoxel-shifts. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2016;76:1574-1581.

24. Tournier JD, Smith R, Raffelt D, Tabbara R, Dhollander T, Pietsch M, Christiaens D, Jeurissen B, Yeh CH and Connelly A. MRtrix3: A fast, flexible and open software framework for medical image processing and visualisation. NeuroImage. 2019;202:116137.

25. Nilsson M, Szczepankiewicz F, van Westen D and Hansson O. Extrapolation-Based References Improve Motion and Eddy-Current Correction of High B-Value DWI Data: Application in Parkinson's Disease Dementia. PloS one. 2015;10:e0141825.

26. Morez J, Sijbers J, Vanhevel F and Jeurissen B. Constrained spherical deconvolution of nonspherically sampled diffusion MRI data. Human brain mapping. 2021;42:521-538.

27. Szczepankiewicz F, Westin CF and Nilsson M. Gradient waveform design for tensor-valued encoding in diffusion MRI. J Neurosci Methods. 2021;348:109007.

28. Sjolund J, Szczepankiewicz F, Nilsson M, Topgaard D, Westin CF and Knutsson H. Constrained optimization of gradient waveforms for generalized diffusion encoding. Journal of magnetic resonance. 2015;261:157-68.

Figures

Figure 1. Effective diffusion encoding gradient waveforms for linear (top) and planar (bottom) b-tensor encoding, with up to 2nd order motion-nulling and b = 1 ms/µm2. Other sequence features omitted for clarity. Waveforms were generated using a modified NOW toolbox28.

Figure 2. Registered images in a single short-axis slice collected with linear and planar tensor encoding, at b = [0.1, 0.2, 0.5, 1.0] ms/µm2 along [10, 10, 10, 20] rotations.

Figure 3. (Right) Normalised signal attenuation curves for linear (green; bΔ = 1) and planar (orange; bΔ = -0.5) tensor encoding in the myocardium (left). Signals averaged across ROI and used to fit a covariance model. Data points acquired across b = [0.1 0.2 0.5 1.0] ms/µm2.

Figure 4. S0 image and parameter maps in one healthy volunteer including mean diffusivity (MD; in µm2/ms), fractional anisotropy (FA), microscopic FA (µFA), isotropic, anisotropic and total mean kurtosis (MKi, MKa, MKt) and colour FA (CFA) map.

Table 1. Parameter values within ROIs in the myocardial wall in a single mid-short-axis slice of one healthy volunteer. Mean ± SD across voxels in the ROI.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)
0017
DOI: https://doi.org/10.58530/2022/0017