0014
Real-time myocardial landmark-tracking for MRI-guided cardiac radio-ablation using Gaussian Processes
Niek R.F. Huttinga1, Osman Akdag1, Martin Fast1, Joost Verhoeff1, Alessandro Sbrizzi1, and Stefano Mandija1
1Department of Radiotherapy, Computational Imaging Group for MR therapy & Diagnostics, University Medical Center Utrecht, Utrecht, Netherlands
1Department of Radiotherapy, Computational Imaging Group for MR therapy & Diagnostics, University Medical Center Utrecht, Utrecht, Netherlands
Synopsis
Accurate tracking of lesions within or near the heart presents a unique challenge due to cardiorespiratory motion during stereotactic radiotherapy. Mitigating this motion is essential to limit the risk of radiation-induced complications. Here, the feasibility of real-time prospective myocardial landmark-tracking with Gaussian Processes from few k-space readouts is demonstrated on the 1.5T Elekta Unity MR-linac. Retrospective and prospective phantom and in-vivo experiments were conducted in 2D, and preliminary in-silico experiments were done to demonstrate the feasibility in 3D. Results indicate high accuracy, and thereby great potential for real-time 3D myocardial target tracking for cardiac radio-ablation.
Introduction
During stereotactic radiotherapy, accurate targeting of lesions within/near the heart presents a unique challenge due to cardiorespiratory motion. Unmitigated motion blurs the prescribed radiation dose beyond the target lesion, thus increasing the risk of radiation-induced complications.MR-linacs currently support 2D-cine MR-based respiratory motion estimation at 4-8Hz. However, 3D motion management at this speed during cardiac radio-ablation[1] for ventricular tachycardia (VT) patients is not sufficient.
Here, we apply a previously introduced framework based on Gaussian Processes (GPs) for real-time myocardial landmark-tracking, i.e. tracking spatial coordinates of target landmarks[2,3]. The framework requires only few readouts of k-space data, and therefore has the potential to perform myocardial landmark-tracking at sufficiently high framerate (>100Hz), suitable for cardiac radio-ablation. In this proof-of-concept, we demonstrate the method in 2D on a phantom and in-vivo (healthy volunteers and a VT patient), and in 3D on simulations with a digital phantom, with the ultimate future goal of 3D prospective myocardial target tracking on a 1.5T Unity MR-linac.
Theory
GPs are frequently applied to regression problems; they learn from a set of function values $$$f(x_1),f(x_2),…,f(x_N)$$$, and then estimate unobserved function values and confidence intervals at new measurement locations, i.e. $$$f(x_{N+1}),f(x_{N+2}),…$$$. This inference can be performed in few milliseconds from few data, making it very suitable for radiotherapy applications.Here, we define the problem of tracking anatomical landmarks directly from k-space data and apply a GP to solve it. First, given a training set of landmark locations $$$f(X_D)$$$ and fast k-space readouts $$$X_D$$$, a GP is trained in 10 seconds. Next, the trained GP is applied to infer landmark locations from rapidly acquired k-space readouts $$$X_Q$$$ in a hold-out test set. The end-to-end acquisition+processing step takes few milliseconds.
Methods
GP details[3]Application of GPs requires a training set (here: myocardial landmarks). These landmarks are obtained with template matching (TM)[4]. The GP inputs are two mutually orthogonal spokes in 2D, and three in 3D, either retrospectively simulated or prospectively acquired. This can typically be acquired within 10ms, yielding a framerate of >100Hz. Training was performed in 10 seconds on the first half of all dynamics, testing was performed on the last half in milliseconds per dynamic. Results were visually compared with TM as independent reference, and through the root-mean-square-distance (RMSD) the end-point-distance (EPD) (Euclidean distance between vectors) metrics.
Experiments
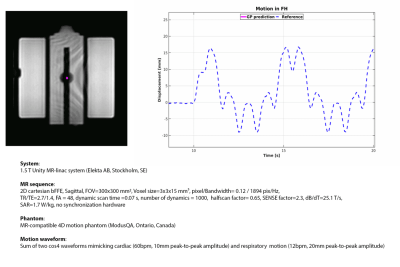
First, the feasibility for GP-based myocardial landmark-tracking was retrospectively validated with 2D cine-MRI of an MR-compatible 4D motion phantom (details: Fig.1).
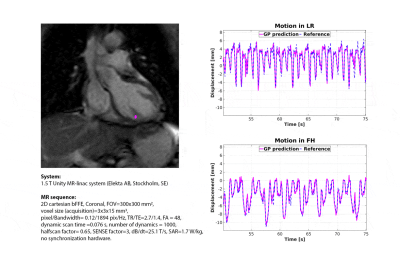
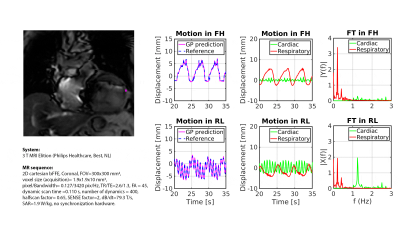
Second, retrospective myocardial landmark-tracking was demonstrated in a healthy volunteer and on a patient with cardiac arrhythmia, scheduled for cardiac radio-ablation (details: Fig.2,3).
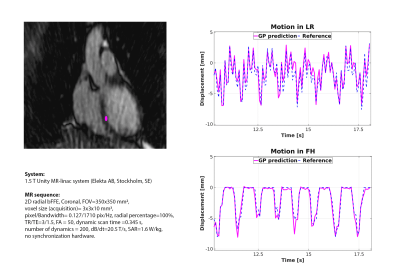
Third, prospective myocardial landmark-tracking was investigated for a healthy volunteer. A 2D uniform radial cine-MRI was acquired (details: Fig.4), and GP inputs were extracted from raw MR-data.
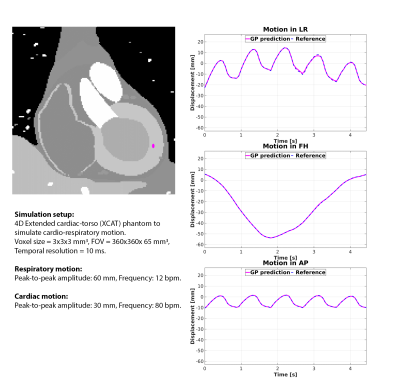
Finally, the extension to 3D landmark-tracking was investigated using the XCAT phantom (details: Fig.5). The phantom and in-vivo volunteer data were acquired on a 1.5T Unity MR-linac, the patient data on a clinical 3T MRI.
Results
Fig.1 shows the GP prediction and its comparison with TM on the phantom measurements. The low RMSD (0.2mm) and EPD (0.3±0.2mm) demonstrate the capability to retrospectively perform myocardial landmark-tracking in good agreement with TM.Sub-voxel differences with respect to TM were obtained for the healthy volunteer (RMSD-FH=0.8mm; RMSD-LR=0.6mm; EPD=0.5±0.6mm) and the patient (RMSD-FH=0.4mm; RMSD-LR=0.3mm; EPD =0.3±0.2mm) (Fig.2 and 3).
Additionally, Fig.3 shows that cardiac and respiratory motion components can be extracted from the GP estimates. The cardiac frequency peak at 1.3Hz matches the measured heart-rate of the patient ($$$\sim$$$80 beats-per-minute).
Fig.4 shows the prospective GP estimates and the comparison with TM on a healthy volunteer. The good agreement between GP and TM (RMSD-FH=0.4mm; RMSD-LR=0.6mm; EPD=0.6±0.4mm) demonstrates the capability of GP to perform myocardial landmark-tracking with similar accuracy as TM, but with >100Hz framerate.
Fig.5 shows retrospective 3D GP estimates for 3D simulated data from a digital XCAT phantom. Sub-voxel agreement with TM is obtained (RMSD-FH=0.1mm; RMSD-LR=0.4mm; RMSD-AP=0.1mm; EPD=0.2±0.1mm), indicating the potential extension to in-vivo 3D myocardial landmark-tracking.
Discussion & Conclusions
In this work, we have demonstrated the feasibility of myocardial landmark-tracking on a phantom, healthy volunteers and a VT patient. We have also demonstrated the feasibility to prospectively perform myocardial landmark-tracking on a Unity MR-linac. Ultimately, we have demonstrated in-silico the feasibility of an extension to 3D. In practice, however, a 3D extension would require an in-vivo training set with 3D landmark targets and further validations in clinical settings. This will be subject of future work.The proposed method has the potential to aid an MR-linac radiotherapy workflow both before (e.g., motion estimation for treatment planning) and during radiation (motion management, treatment control). Moreover, given the high potential temporal resolution in 3D (>100 Hz theoretically achievable with only three readouts as inputs), our approach may be relevant for VT patients, where VT storms may occur during treatment. Such VT episodes would lead to high standard-deviations in the GP prediction, which could prospectively be used to temporarily halt the treatment for safety reasons[3].
Ultimately, these first results on a VT patient seem to demonstrate robustness to imaging artifacts introduced by cardiac implant devices, specifically indicating the method’s potential for cardiac radio-ablation on VT patients.
Acknowledgements
The authors thank dr. P. Borman, dr. T. Schakel, dr. Ir. T. Bruijnen for patching the Unity MR-linac scanner to enable data export and technical support in the research project; dr. S.M.G. van de Pol, dr. F.A.A. Mohamed Hoesein, and dr. R.J. Hassink for clinical support.References
[1] Cuculich, P, et al. “Noninvasive Cardiac Radiation for Ablation of Ventricular Tachycardia. N Engl J Med, 2017, doi: 10.1056/NEJMoa1613773.
[2] Sbrizzi, A, et al. “Acquisition, reconstruction and uncertainty quantification of 3D non-rigid motion fields directly from k-space data at 100 Hz frame rate”, Proc. Intl. Soc. Mag. Reson. Med. 27, 2019: #0795.
[3] Huttinga, NRF et al. “Joint 3D motion-field and uncertainty estimation at 67Hz on an MR-LINAC", Proc. Intl. Soc. Mag. Reson. Med. 29, 2021: #4552.
[4] Akdag, O, et al. “Feasibility of free breathing real-time cine-MRI for MR-guided cardiac radioablation on the Unity MR-linac", Proc. Intl. Soc. Mag. Reson. Med. 29, 2021: #4014.
Figures
Fig. 1: Cartesian 2D cine-MRI images were acquired using a motion phantom consisting of a static box, and moving cylinder with a spherical insert. A GP was trained to track the magenta-marked myocardial target from two simulated k-space spokes along FH and LR. Template-matching with a circle Hough transform was performed on the insert to train and validate the GP. The figure shows estimates on test samples.
Fig. 2: Coronal Cartesian 2D cine-MRI images were acquired in a healthy volunteer on a 1.5T Unity MR-linac system. A GP was trained to track the magenta-marked myocardial target from two simulated k-space spokes along FH and LR. Template matching was performed to train and validate the GP. The figure shows estimates on test samples.
Fig. 3: Coronal Cartesian 2D cine-MRI images were acquired in a patient carrying a CIED. A GP was trained to track the magenta-marked myocardial target from simulated FH and LR k-space spokes. Template matching was performed to train and validate the GP. The estimated motion pattern was decomposed in cardiac/respiratory motion, and the frequency spectra are shown. Clear peaks can be observed in respectively cardiac/respiratory frequency ranges. The figure shows estimates on test samples.
Fig. 4: Coronal radial 2D cine-MRI images were prospectively acquired in a healthy volunteer. A GP was trained to track the magenta-marked myocardial target. A single channel of raw k-space data of two prospectively acquired spokes along approximately FH and LR were selected as input. Template matching was performed to train and validate the GP. The figure shows estimates on test samples.
Fig. 5: The XCAT digital phantom was used to simulate 3D cardiorespiratory motion. Data were simulated along FH, AP, LR spokes by computing projections over the image, and a GP was trained to track the magenta-marked myocardial target from the three spokes. The GP was trained and validated on ground-truth landmark locations resulting from the simulations. The figure shows estimates over both training (first half), and testing (second half) data for the 3D landmark coordinates.
DOI: https://doi.org/10.58530/2022/0014