Background:

Diffusion imaging techniques have become a major part of diagnostic imaging today. MR Radiographers/Technologists around the world use them daily yet, the various types of diffusion pulse sequences and the concept of diffusion itself are often not well understood. The purpose of this abstract is to help describe the basic fundamentals of diffusion and how they are applied to MR imaging

Teaching Points:

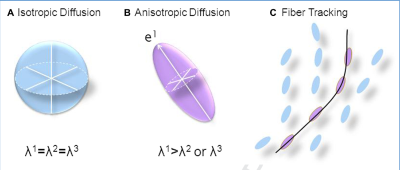
Diffusion is a physical process that refers to the net movement of molecules in a random translational motion from a region of high concentration to one of lower concentration due to thermal energies of the molecules, which is often referred to as Brownian Motion [1]. In MRI we are referring to the movement of water molecules over time. In a free, unrestricted medium, molecules move randomly over time and over a three-dimensional (3D) space that can be calculated assuming a 3D gaussian distribution [2]. The statistical distance of random travel is described by a diffusion coefficient (D) [3]. The technical innovations needed to merge diffusion statistics with MR imaging did not occur until the 1980’s with the first DWI images of the brain presented at the 1985 London SMRM Meeting by Le Bihan [4]. In order to better describe the complex diffusion found in biological tissues on a voxel scale, Le Bihan introduced the statistical parameter apparent diffusion coefficient (ADC) [5]. The ADC is calculated from scans performed at different b values. ADC reflects the degree of diffusion (movement) of water molecules through tissues. The “b value” is key to the diffusion sequence, which is based on the time course and intensity of the magnetic field pulses. Higher b values are more sensitive to diffusion, but also have low signal to noise (SNR). The pulse sequences used to acquire diffusion are usually echo planar or fast gradient recalled echo scans acquired in a set, one without the diffusion gradients and one with the diffusion gradients in order to eliminate the contribution from T1 and T2 weighting and calculate the ADC maps of the diffusion in a voxel by voxel basis [6]. The first part of the sequence pair is most commonly referred to as the “b-0” component that is used to separate the diffusion background from the diffusion measurement acquisition part. The T2 component in diffusion imaging can be significant and sometimes prolonged, resulting in a hyperintensity on the images referred to as T2 shine-through. The ADC maps helps to determine if the hyperintensity on a DWI is from true reduction in diffusion or T2 shine through [7]. DWI techniques can be quite helpful in clinical imaging, especially in tumor characterization and cerebral ischemia where assessment of microcirculation can help characterize areas of free and restricted water movement. The thought of looking at restriction of movement, displacement, and tortuosity of structural compartments was speculated by many and eventually lead to the concept of anisotropy or directional water movement. In 1994, the diffusion tensor was described by Basser, Mattiello and Le Bihan as a mathematical way to characterize anisotropic diffusion [8] (Figure 1). Diffusion Tensor Imaging (DTI) is based on a Gaussian model, just as DWI, in that it describes the diffusion of water molecules assuming a Gaussian description of the movement of the water molecules but it looks at the displacement in all directions. A symmetric tensor of diffusion along each axis with correlation of displacements along each axis was described that became known as the diffusion tensor vectors. There are three eigenvalues (or diffusivities) and three eigenvectors (principal directions) associated with tensor concept that define the movement frame through their magnitude of diffusivity. The diffusion tensor model allowed for the development of more mathematical descriptions that we use in diffusion such as fractional anisotropy (FA), mean diffusivity (MD), axial diffusivity (AD), and radial diffusivity (RD) [8,9]. DTI is able to collect a combination of factors such as the mean diffusion, the degree of anisotropy and the direction of a fiber which has enabled fiber maps and tractography. Basic DTI is limited in that it cannot discern multiple fibers running in multiple directions within a single voxel. For techniques such as fiber tracking, the individual voxels are then connected to each other by mathematically connecting the adjacent voxels. Diffusion MRI has grown into a whole host of techniques including non-Gaussian techniques to try to predict the changes to microstructure on a nanometer range while our images are on the millimeter range. Among the newer diffusion are Diffusion Kurtosis Imaging (DKI), Q-Space, Diffusion Spectral Imaging (DSI), Q-ball, and Quasi-diffusion magnetic resonance imaging (QDI) [8-12] as researchers strive to explore microstructure and the structures of the human body

Summary:

Diffusion imaging is common in modern MRI examinations and looks at the random movement of water molecules over time. Diffusion weighted imaging evolved first, defining b values and the apparent diffusion coefficient for MRI. DWI/ADC is used clinically to detect acute stroke, purulent fluid, and hypercellular tumor. The interest to evaluate the microstructure of neural tissues has allowed the field of diffusion to grow into tensor imaging and beyond.

Acknowledgements

Disclaimer: The opinions and assertions expressed herein are those of the author(s) and do not necessarily reflect the official policy or position of the Uniformed Services University or the Department of Defense.