4296
Improving tractography Reconstruction using Local-phase Features1Department of Medical Physics and Biomedical Engineering, Tehran university of Medical Science, Tehran, Iran (Islamic Republic of), 2Quantitative MR Imaging and Spectroscopy Group, Research Center for Molecular and Cellular Imaging, Tehran, Iran (Islamic Republic of)
Synopsis
Tractography of the brain fibers from diffusion signals in magnetic resonance imaging needs to be more sensitive to structures of diffusion images to reduce the number of ODF used to predict tracts and avoid determining false-positive cases in pixels whose values may have changed due to noise or other unwanted factors. The local-based methods can be improved tractography results. In this abstract, we designed a mask based on the local structures of the diffusion phantom images in 64 directions. Using this mask we reduced the number of gradients and false-positive predicted results from the outputs of the tractography algorithm.
Introduction
Despite the increase in the number of methods for detecting brain fibers, it is still not possible to say with certainty which the method offers the best possible answer. Based on the limitations of DTI modeling and classic tractography algorithms, many articles are geared towards using the HARDI-based tractography method [Tuch (2002); Hagmann et al. (2004)]1,2 determined the principal direction of the diffusion ODF computed from DSI by using a streamlined algorithm. Moreover, to compute more complex fiber configurations, [Parker and Alexander (2003)]3 used a mixture of Gaussian densities, and similarly in their algorithm, [Campbell et al. (2006)]4 offered an extension of the streamlined approach with curvature constraint that predicts fibers crossing according to the QBI model that Tuch had introduced before and Descoteaux et al. (2007)5 proposed another extension to streamlined tractography based on the multiple maxima information of the fiber ODF. From this fiber ODF, they extracted all available maxima and allow for splitting in multiple directions at each step. In this study, first, a physical phantom was constructed based on the placement of nerve fibers introduced in6 and several water-permeable threads were used to build the paths. The phantom images were obtained in 64 directions and 3 slices. First, the local frequency of each image was calculated in different slice directions. The mean values of each image had smaller values and were replaced by zero, and the remaining pixels were used as the input address of the tractography algorithms to calculate the odds. The output was such that each pixel with a non-zero local frequency value had its address and number in the original image was selected and its pixel value in the the original image was sent as input to the tractography algorithm, and finally the general shape of the fibers in the phantom was determined using the Hough transform 7.Material and methods
The image model based on local phase information is I(x)=A(x)cos(φ(x))+I 8. We use a Poisson filter kernel with a subtraction spherical filter with values of lambda = 10 and ratio = .98. We designed as follows that the Fourier transform of diffusion images in different directions and slices are given as the input of this filter. The output is p=[(diffusion Images)© DOP] and q=[(diffusion Images)© (icosΦφ,isinφ) DOP). We will have f≡(gradient(φ)).n=(p.gradient(q)-q.gradient(p))/(p′2+abs(q)′2) and n=[cosθ,sinθ].Next, we designed a mask whose values of each pixel represent information about the local structures of the image, and finally, this the mask is multiplied in the images obtained from the diffusion model.Mask(x,y)=0, if (local f Matrix)(x,y)<mean(local f Matrix(:,:)); otherwise Mask=1.
The relation above states that if the value of the Mask in each pixel is equal to one, that pixel represents the local structure of the image, this local structure can represent a line or an edge. Finally, the main image is multiplied in different directions in pixels by pixels in the designed mask so that only pixels are selected as the input of the tractography algorithm, which represents significant changes and values as a local structure. In this work, we use Q-ball Imaging (QBI) [Tuch, 2004] 9. Here we use the normalized and dimensionless ODF estimator in QBI, derived in [Aganj et al., 2010] 10
Experimental results and discussion
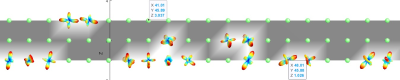
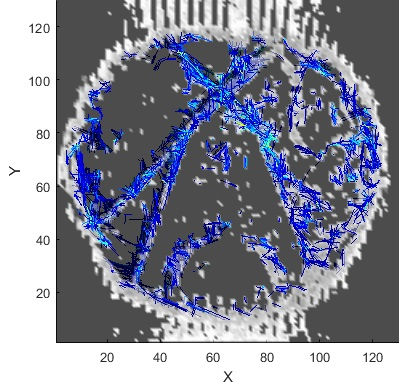
It is well known that one of the goals of diffusion imaging reconstruction is to obtain the most complex tracts by applying the lowest gradient directions. Here we used the mask that was presented in the section before. At the heart of our algorithm is a quadrature filter with lambda = 10 and ratio = .98, the output of which is convoluted with the diffusion images obtained from the phantom to determine the local phase features that indicate the number of changes in the gray levels of the images. These changes indicate the structures in the images, where the structures are the same as the fibers. On the other hand, inside a voxel, the diffusion of water molecules along the fibers can be imaged by applying gradients, so if the tractography is in the direction of local structures of images, the number of ODF required to implement the trajectory algorithm was reduced (Figure 3.b.). Therefore, it can be concluded that it is not necessary to use all 64 gradient directions for diffusion images shown in Figure 1 and we need to use only the certain directions that the outputs of the mask determine for us. Figure 4 is the output of the mask applied to the images obtained from the phantom (Figure 1), according to which it can be seen that the most complex configuration predicted in the phantom (U-shape) has been correctly detected.Conclusions
Reconstruction of multi-fiber imaging in the brain using the mathematical model of the signal distribution function in three parts is performed as follows. In part one, presenting a mathematical model of the signal of diffusion of water molecules in the white matter of the brain by Q-ball imaging. In the second part, designing and presenting a new tractography algorithm based on the signal model obtained from the local phase features. Finally, Designing and manufacturing a physical phantom to evaluate the results obtained from previous steps.Acknowledgements
No acknowledgement found.References
1-Tuch, D., Reese, T., Wiegell, M., Makris, N., Belliveau, J., & Wedeen, V. (2002). High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity. Magnetic Resonance in Medicine, 48, 577–582.
2- Hagmann, P., Thiran, J.P., Jonasson, L., Vandergheynst, P., Clarke, S., Maeder, P., Meuli, R., 2003. DTI mapping of human brain connectivity: statistical fiber tracking and virtual dissection. NeuroImage 19, 545–554.
3-Parker GJ, Alexander DC. 2003. Probabilistic Monte Carlo based mapping of cerebral connections utilizing whole brain crossing fiber information. Info Process Med Imaging 18:684–695.
4- Campbell, J.S.W., Savadjiev, P., Siddiqi, K., Pike, G.B., 2006. Validation and regularization in diffusion MRI tractography. Third IEEE International Symposium on Biomedical Imaging (ISBI): from Nano to Macro. IEEE, Arlington, Virginia, USA, pp. 351–354.
5- Descoteaux, M., Angelino, E., Fitzgibbons, S., Deriche, R., 2007. Regularized, fast, and robust analytical q-ball imaging. Magnetic Resonance in Medicine 58, 497–510.
6- Poupon, C., Rieul, B., Kezele, I., Perrin, M., Poupon F., Mangin, J.F. 2008. New diffusion phantoms dedicated to the study and validation of high-angular-resolution diffusion imaging (HARDI) models. Magnetic Resonance in Medicine, 60(6), 1276-83.
7- Aganj, I. et al. 2011. A Hough transform global probabilistic approach to multiple-subject diffusion MRI tractography. Medical image analysis 15, 414–425.8- Tuch, D., 2004. Q-ball imaging. Magnetic Resonance in Medicine 52, 1358–1372.
9- Felsberg M." Optical Flow Estimation from Monogenic Phase" in Proc. 1st Int. Conf. Complex Motion, pp. 1–13, 2004.
10- Aganj, I., Lenglet, C., Sapiro, G., Yacoub, E., Ugurbil, K., Harel, N., 2010. Reconstruction of the orientation distribution function in single and multiple shell q-ball imaging within a constant solid angle. Magnetic Resonance in Medicine. 64 (2), 554–566.