Introduction

There are several applications of tractography such as helping in brain surgery or studying the effects of disease on brain connectivity across populations. To extract specific white matter bundles from whole-brain tractogram and performing inter or intra-group analyses on them, we need to align data from all subjects to a common reference. In this paper, we introduce the StND method for non-rigid tractography registration. StND first linearly registers the two given bundles and then performs high-level deformations for better alignment of white matter bundles.

Methods

Given two bundles, static bundle, and moving bundle, StND performs non-rigid streamline registration to align the moving bundle with the static bundle. Let $$$S_{i}$$$ be a streamline and $$$T$$$ a tractogram/tract. $$$T = \{S_{1}, S_{2},..., S_{n}\}$$$, $$$S_{i} \in T$$$, $$$S_{i} = \{s_{1}, s_{2},..., s_{n}\}$$$, where $$$s_{i}$$$ is a 3D vector point. Streamlines in T can have different numbers of points. StND linearly registers two bundles using streamline-based linear registration (SLR)¹. SLR helps in finding the first correspondence among streamlines of two tracts. StND then converts streamline data from static and linearly registered moving bundle into 3D data points sets. In order to treat tractography data as a 3D point-set registration problem. We get all the points in $$$T$$$ and save information of the streamline index of each point in a separate index list (which is used to bring 3D points back into streamline-space). Point-set $$$P$$$ becomes a list of 3D point vectors from all streamlines $$$P = \{s_{1}, s_{2},..., s_{n}\}$$$. It applies the Coherent Point Drift (CPD)^2,3 on two point-sets to perform high-level deformations. The CPD algorithm takes a probabilistic approach to aligning two point-sets. Registration is formulated as a maximum-likelihood estimation problem using the Gaussian-Mixture-Model (GMM) method. The points in the moving set are considered as the GMM centroids and the static point-set represents the data points generated by the GMM. The GMM centroids from the moving point-set are fitted to the static point-set by maximizing the likelihood. When the two point-sets are optimally aligned, the correspondence is the maximum of the GMM posterior probability for a given data point. To preserve the topological structure of the point-sets, the GMM centroids are forced to move coherently as a group. The expectation-maximization algorithm is used to optimize the cost function. The CPD method concurrently finds the nonrigid transformation and the correspondence amongst two point-sets using motion coherence theory⁴. After nonrigid registration, 3D point-set data is converted back to the original streamline space. Points are ordered into streamlines by using point-streamline-index information saved in the index list.

Results

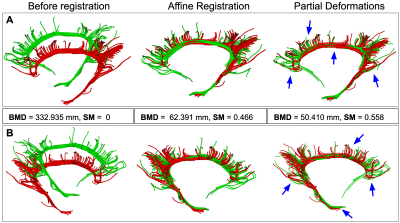
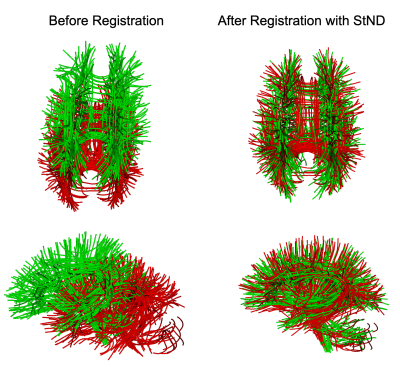
Results of StND registration on two Cingulum bundles are shown in Fig.1. We used a high value of regularization parameter $$$\lambda$$$ = 0.8 for nonrigid registration as we do not want to completely change the structure of the original bundle by deforming it too much. Smoothness parameter $$$\beta$$$ was set to 20. In Fig.1, A shows the front and B shows the back view of Cingulum bundles. Where the red bundle is static and the green bundle is a moving bundle. Blue arrows point towards the areas of improved results with nonrigid registration. Note that the original anatomical structure of the bundle is preserved after deformations. The quality of registration is assessed by calculating Bundle-based Minimum Distance (BMD)¹ and Bundle Shape Similarity Score (SM)⁵ between bundles. BMD decreases and SM increases as we register two bundles together as shown in Fig.1. For this experiment, it took 11.59 seconds to run StND on a 2.3 GHz Intel Core i5 system. We can also register the whole brain tractograms with the StND method as shown in Fig.2.

Discussion

The optimal expected output of nonrigid tract registration is non-trivial to decide. The same type of white matter bundle can have different shapes and sizes for different subjects. Deforming the original anatomical shape of the bundle is not necessarily ideal as it can lose its characteristics needed in the analysis. For example, a patient with a tumor will have some pathways missing from the area of tumor location. Deforming the shape of the bundle too much, in this case, can lead to undetected abnormalities/tumor in the analysis. StND provides the user the option to decide how much they want to deform the bundle by changing the values of $$$\lambda$$$ and $$$\beta$$$. Where $$$\lambda$$$ controls the trade between regularizing the deformation and having points match very closely. The lower the value of $$$\lambda$$$ the more closely the point-sets would match. $$$\beta$$$ controls the smoothness of the deformation.

Conclusion

White matter tract registration is a crucial step for individual or group analysis of white matter tracts. Many registration algorithms try to deform completely one structure to the other trying to fit exactly the target step. That could be catastrophic for tractography applications as many of the bundles could have erroneous streamlines driving the registration into an anatomically impossible shape. In this paper, we introduced a non-rigid registration method that allows for partial deformations to better align two tracts as compared to linear or image-based non-rigid registration. We use partial deformation because in that way the anatomy corresponds more naturally/logically accurate rather than completely warping one shape to another.

Acknowledgements

We would like to acknowledge that research reported in this publication was supported by the National Institute Of Biomedical Imaging And Bioengineering of the National Institutes of Health under Award Number R01EB027585.