4285
ODF-Fingerprinting Improves Reconstruction of Fibers Crossing at Shallow Angles: A Study on Diffusion Phantom1Center for Advanced Imaging Innovation and Research (CAI2R), NYU School of Medicine, New York, NY, United States, 2Psychology Software Tools, Inc., Pittsburgh, PA, United States, 3Department of Neurosurgery, Perlmutter Cancer Center, Neuroscience Institute, Kimmel Center for Stem Cell Biology, NYU School of Medicine, New York, NY, United States, 4University of Pittsburgh, Pittsburgh, PA, United States
Synopsis
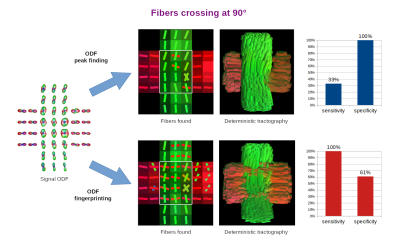
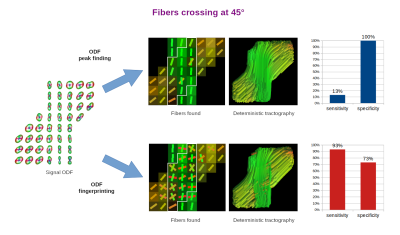
ODF peak finding typically fails to reconstruct fibers crossing at angles below 45 degrees. We aim to break this barrier with ODF-Fingerprinting. Our approach replaces the peak finding mechanism with pattern matching, allowing to use all the information stored in ODFs. In this work, we study the ability of ODF-Fingerprinting to reconstruct fibers crossing at 90, 45, and 30 degrees in a diffusion phantom composed of textile tubes with 0.8µm diameter, approaching the anatomical scale of axons. Our approach reaches much higher sensitivity (84-100%) than the ODF peak finding (0-33%), especially at the shallow angles.
Introduction
Most tractography algorithms rely on identification of peaks in Orientation Distribution Functions (ODFs) to reconstruct white matter fibers from Diffusion Weighted Images (DWIs) [1,2,3]. However, the ODF peak finding approach lacks precision in determining crossing fibers, especially when they cross at shallow angles [2,3]. ODF-Fingerprinting (ODF-FP) [4] alleviates this issue by replacing the peak finding mechanism with pattern matching. For any given ODF calculated from a DWI, our method seeks the closest match in a precomputed ODF-dictionary composed of synthetically generated samples. This modification allows to use all the information stored in an ODF to reconstruct crossing fibers, rather than to rely solely on finding ODF peaks.In this work, we study the ability of ODF-FP to reconstruct fibers crossing at 90°, 45°, and 30° in a Taxon™ (textile water filled tubes) anisotropic diffusion phantom [5]. The phantom contains microtubes with $$$0.8~$$$µm diameter, approaching the anatomical scale of axons found in the human brain, thus providing ground truth information for tractography. Having this, we compare ODF-FP and the ODF peak finding approach in determination of crossing fibers. The ability to reconstruct them correctly is crucial in the human brain for tractography-based surgical planning [3] and measurements of brain structural connectivity [1,2,3].
Methods
Data:We scanned the phantom (Figure 1) at $$$2\times2\times2~$$$mm resolution, $$$TE/TR=74/8000~$$$ms, using a multishell diffusion protocol with $$$b=1000,2000,3000~$$$s/mm2, 90 directions each, interleaved with 20 images at $$$b=0$$$. Then, we ran Generalized Q-space Imaging (GQI) [6] reconstruction of ODFs, implemented in DSI-Studio [7], choosing a uniform 321-point tessellation of a unit hemisphere to obtain discrete ODF samples. From that, we reconstructed fiber configurations by finding local maxima of ODFs (also in DSI-Studio).
ODF-Dictionary:
We generated an ODF-dictionary (Figure 2) holding 100,000 random configurations of 1 or 2 fibers simulated with a multicompartment diffusion model [8]:
$$S(b)=S(0)\cdot\left[p_{iso}e^{-bD_{iso}}+\sum_{i=1}^{2}p^{(i)}\kappa^{(i)}(b,\mathbf{g}\cdot\mathbf{n}^{(i)})\right],$$
where $$$S(0)$$$ is the signal without diffusion encoding ($$$b = 0$$$), while the contribution of $$$i$$$-th fiber ($$$i = 1,2$$$) is defined as
$$\kappa^{(i)}(b,\mathbf{g}\cdot\mathbf{n}^{(i)})=f^{(i)}e^{-bD^{(i)}_{a,\parallel}(\mathbf{g}\cdot\mathbf{n}^{(i)})^2}+\left(1-f^{(i)}\right)e^{-bD^{(i)}_{e,\parallel}(\mathbf{g}\cdot\mathbf{n}^{(i)})^2-bD^{(i)}_{e,\perp}\left(1-(\mathbf{g}\cdot\mathbf{n}^{(i)})^2\right)},$$
where $$$\mathbf{n}^{(i)}$$$ is the fiber orientation (chosen from 321 directions defined by the tessellation) and $$$\mathbf{g}$$$ is the direction of the diffusion encoding gradient.
To ensure sufficient coverage of the parameter space, the volumes of free water $$$p_{iso}\in[0,0.2]$$$ and neurites $$$p^{(1)},p^{(2)}\geq0.2$$$ were drawn randomly with a uniform distribution ensuring that $$$p_{iso}+p^{(1)}+p^{(2)}=1$$$. Analogously, we randomized the fraction sizes $$$f^{(i)}\in[0.3,0.8]$$$ and respective diffusivities: free water $$$D_{iso}\in[2,3]$$$, intra-axonal $$$D^{(i)}_{a,\parallel}\in[1.5,2.5]$$$, and extra-axonal $$$D^{(i)}_{e,\parallel}\in[1.5,2.5],D^{(i)}_{e,\perp}\in[0.5,1.5]$$$. The b-values and gradient directions mirrored the DWIs' acquisition protocol.
Evaluation:
In order to quantify the results, we selected one slice of the acquired image and manually defined ROIs representing ground truth areas of single and crossing fibers at 90°, 45°, and 30° (Figures 3-5, respectively). In all tested cases, we applied the same Quantitative Anisotropy (QA) filtering threshold QA < 0.66 (automatically adapted by DSI-Studio) to eliminate artifacts caused by noise.
Finally, we classified each successful reconstruction of a crossing fiber configuration as true positive (TP) and each successful reconstruction of a single fiber as true negative (TN). The remaining voxels were classified as false negatives (FN) and false positives (FP), respectively. From these, we computed the sensitivity and specificity measures as follows:
$$sensitivity=TP/(TP+FN),\quad specificity=TN/(TN+FP).$$
Results
The reconstruction of fibers in the studied diffusion phantom posed a challenging task due limited angular resolution of the acquisition and intrinsic ODF peak width [1,9]. Unsurprisingly, the most difficult cases were the 30° and 45° crossings.The ODF peak finding approach failed to reconstruct most of the 30° and 45° crossings, since it merged them into a single fiber. This resulted in extremely low sensitivity (0-33%) and very high specificity (100%). On the contrary, ODF-FP successfully identified the majority of crossing fibers (84-100% sensitivity), although it tended to produce spurious fibers in the single fiber voxels (47-73% specificity).
Discussion
ODF peak finding is an inherently limited method for fiber identification, as it typically fails when the fibers cross at angles below 45° [2,3,10]. ODF-FP aims to break this barrier. By matching the entire traces of ODFs with the precomputed ODF-dictionary, our approach can identify fibers crossing at shallow angles, where neighboring ODF peaks merge and become indistinguishable for peak finding algorithms (Figures 2b and 5). The latter behavior has a strong impact on the human brain tractography, especially when reconstructing cortical terminations of fascicles [2,3] or thin cranial nerves [11].The diffusion phantom used in this study provided human-like ground truth data representing fibers crossing at 90°, 45°, and 30°. Our experiments showed that ODF-FP was more capable of reconstructing these crossings than the ODF peak finding approach. Even though the presented sensitivity and specificity measures (Figures 3-5) implicitly depended on the selected QA < 0.66 threshold, the outperformance of ODF-FP was evident.
The experiments highlighted a limitation of our approach which resides in the ODF-dictionary. When using ODF-FP, it is crucial to ensure that the synthetically generated ODFs meet the characteristics of the input signal. Here, we chose the multicompartment diffusion model with relatively broad parameter ranges to cover a large spectrum of possible fiber configurations. Fine-tuning of the above to the specifics of the phantom microtubes could decrease the number of false positives, although it would limit the universality of the ODF-dictionary.
Acknowledgements
This project is supported in part by the National Institutes of Health (NIH, R01-NS082436, R01-EB028774, and NIH/NINDS, R44-NS103729). This work was performed under the rubric of the Center for Advanced Imaging Innovation and Research (CAI2R, https://www.cai2r.net), a NIBIB Biomedical Technology Resource Center (NIH P41-EB017183).References
[1] B. Jeurissen, A. Leemans, J.-D. Tournier, D. K. Jones, J. Sijbers, Investigating the prevalence of complex fiber configurations in white matter tissue with diffusion magnetic resonance imaging, Human brain mapping (2013).
[2] M. Descoteaux, R. Deriche, T. R. Knosche, A. Anwander, Deterministic and probabilistic tractography based on complex fibre orientation distributions, IEEE transactions on medical imaging (2008).
[3] S. Jbabdi, H. Johansen-Berg, Tractography: where do we go from here?, Brain connectivity (2011).
[4] S. H. Baete, M. A. Cloos, Y.-C. Lin, D. G. Placantonakis, T. Shepherd, F. E. Boada, Fingerprinting orientation distribution functions in diffusion MRI detects smaller crossing angles, NeuroImage (2019).
[5] W. Schneider, S. Pathak, Y. Wu, D. Busch, D., J. Dzikiy, Taxon anisotropic phantom delivering human scale parametrically controlled diffusion compartments to advance cross laboratory research and calibration, ISMRM 2019.
[6] F.-C. Yeh, V. J. Wedeen, W.-Y. I. Tseng, Generalized q-sampling imaging, IEEE transactions on medical imaging (2010).
[7] F. Yeh, Diffusion MRI reconstruction in DSI Studio, Advanced Biomedical MRI Lab, National Taiwan University Hospital. Available online at: http://dsi-studio.labsolver.org/Manual/Reconstruction\#TOC-Q-Space-Diffeomorphic-Reconstruction-QSDR (2017).
[8] Y. Assaf, R. Z. Freidlin, G. K. Rohde, P. J. Basser, New modeling and experimental framework to characterize hindered and restricted water diffusion in brain white matter, Magnetic Resonance in Medicine (2004).
[9] A. Barnett, A., Theory of Q-ball Imaging Redux: Implications for Fiber Tracking, Magnetic Resonance in Medicine, (2009).
[10] J. D. Tournier, C. H. Yeh, F. Calamante, K. H. Cho, A. Connelly, C. P. Lin, Resolving crossing fibres using constrained spherical deconvolution: Validation using diffusion-weighted imaging phantom data, Neuroimage (2008).
[11] M. Yoshino, K. Abhinav, F. C. Yeh, S. Panesar, D. Fernandes, S. Pathak, P. A. Gardner, J.C. Fernandez-Miranda, J.C., Visualization of cranial nerves using high-definition fiber tractography. Neurosurgery (2016).
Figures
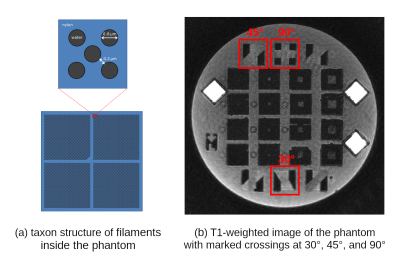
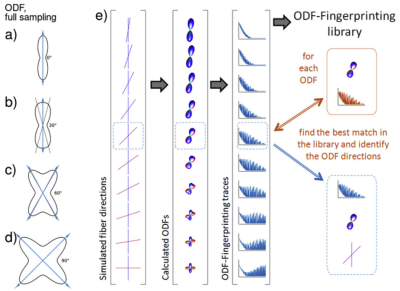
Figure 2. Exact ODFs of a single fiber (a) and two crossing fibers (b-d). The ODF dictionary (e) is composed of synthetically generated ODFs with known fiber configurations. They are matched with the input data by comparing the full ODF traces – rather than seek the ODF peaks – to reconstruct the crossing fibers.