4284

Robust residual bootstrapping algorithm for accurate SH representation of DW MRI signal that contains outliers

Viljami Sairanen^1,2 and Chantal M. W. Tax^3,4
¹Department of Computer Science, University of Verona, Verona, Italy, ²Translational Imaging in Neurology, Department of Medicine and Biomedical Engineering, University of Basel, Basel, Switzerland, ³CUBRIC, Cardiff University, Cardiff, United Kingdom, ⁴Image Sciences Institute, University Medical Center Utrecht, Utrecht, Netherlands

Synopsis

Diffusion MRI measurements are affected by noise which propagates into the model estimation. Residual bootstrapping has been proposed to assess the uncertainty of parameter estimates, but do not consider the confounding effect of measurement outliers (e.g. due to subject motion), limiting their usage on clinical data. We present a robust bootstrapping algorithm and demonstrate its performance on the estimation and uncertainty quantification of rotationally invariant spherical harmonic (RISH) features with simulations and clinical data. Our algorithm can improve the reliability of cross-scanner harmonization relying on RISH and probabilistic tractography.

Introduction

Parameter estimation in diffusion MRI (dMRI) is challenged because of measurement noise. Uncertainty quantification of estimates using techniques such as bootstrapping can provide invaluable information for group comparisons and tractography^1,2. However, bootstrapping commonly ignores the fact that intensity outliers due to e.g. subject motion can have a significant impact on estimates.

Robust techniques^3–6 have been developed to detect and reduce the impact of measurement outliers, by assigning a weight representing the reliability of each measurement or excluding outliers. These efforts have focused on the robust estimation of diffusion tensor imaging and diffusion kurtosis imaging, in which case heteroscedasticity of residuals has to be considered when using the log-transform in weighted linear least squares estimators^4,7,8. This work presents a robust residual bootstrap algorithm for the homoscedastic case, which is evaluated on the estimation and uncertainty quantification of spherical harmonics (SH) and rotationally invariant SH (RISH) features⁹, which are becoming increasingly popular as a dMRI-signal representation e.g. in cross-scanner harmonization¹⁰. Robust uncertainty estimates could, amongst others, increase the reliability of harmonization techniques¹⁰ and probabilistic tractography².

Theory

The SH representation of the dMRI-signal is obtained by solving a linear least squares problem¹¹ (eq. 1):
$$\mathbf{y}=\mathbf{X}\beta+\varepsilon,\tag{1}$$
with measurements $$$\mathbf{y}$$$, design matrix $$$\mathbf{X}$$$, independent and identically distributed errors $$$\varepsilon$$$, and the SH-coefficients $$$\beta$$$. The SH-coefficients should be estimated with weighted linear least squares¹² if the data contains outliers (eq. 2):
$$\hat{\beta}\approx\left(\mathbf{X}^T\mathbf{WX}\right)^{-1}\mathbf{X}^T\mathbf{Wy},\tag{2}$$
where the diagonal of the weight matrix $$$\mathbf{W}$$$ contains measurement reliability-estimates.

Previous SH-bootstrapping methods typically ignore outliers¹¹, and this work proposes a robust homoscedastic bootstrapping algorithm in which the residuals $$$\mathbf{r}\approx\mathbf{y}-\mathbf{X}\hat{\beta}$$$ are adjusted for the reliability of the corresponding measurement $$$\mathbf{y}$$$ stored in $$$\mathbf{W}$$$. The residuals are furthermore adjusted for leverage with the hat matrix¹¹ $$$\mathbf{H}=\mathbf{X}\left(\mathbf{X}^T\mathbf{WX}\right)^{-1}\mathbf{X}^T\mathbf{W}$$$ in eq. 3, resulting in an adjusted residual $$$\tilde{r}_i$$$ for each measurement $$$i$$$:
$$\tilde{r}_i=\frac{r_iW_{ii}}{\sqrt{1-H_{ii}}}.\tag{3}$$
With random resampling of the adjusted residuals $$$\tilde{r}_i$$$, a bootstrap sample $$$y_i^*$$$ can be generated:
$$y_i^*=\mathbf{X}_i\hat{\beta}_i+\tilde{r}_i,\tag{4}$$
where $$$j$$$ is randomly selected from the set $$$[1,...,n]$$$. SH-coefficients of each bootstrap can be estimated using eq. 2 by setting $$$\mathbf{W}=\mathbf{I}$$$ as bootstrap samples have equal reliability.

Methods

Simulations
A synthetic dMRI-signal with crossing fibres was simulated with the StickBall model using dmipy¹³ and the Human Connectome Project’s gradient scheme with a b-value of $$$3000\frac{\mathrm{s}}{\mathrm{mm}^2}$$$ and 90 directions. Stick orientations $$$\left(\theta,\phi\right)$$$ were $$$\left(\frac{\pi}{6},\frac{\pi}{6}\right)$$$ and $$$\left(\frac{\pi}{2},\frac{3\pi}{4}\right)$$$ and their parallel diffusivity $$$1.7\cdot10^{-9}\frac{\mathrm{m}^2}{s}$$$, and the ball isotropic diffusivity was $$$3.0\cdot10^{-9}\frac{\mathrm{m}^2}{s}$$$.

Signal drop-out artefacts were introduced to 0-30% of the signals by decreasing the signal with 100% before adding Rician noise with a signal-to-noise ratio of 20 (2000 realizations). Outlier selection was done by randomly picking a direction and finding the closest directions to mimic a worst-case scenario.

In vivo data
A 3T MRI neonatal dataset with numerous motion artefacts was used to evaluate clinical feasibility. The protocol had 13 non-DW images and two b-values of $$$750\frac{\mathrm{s}}{\mathrm{mm}^2}$$$ and $$$1800\frac{\mathrm{s}}{\mathrm{mm}^2}$$$ with 60 and 74 DWIs respectively. Acquisition parameters were TR 3300ms, TE 103ms, resolution 2mm3 isotropic, and multi-slice acceleration 2. DWIs were processed using ExploreDTI¹⁴ with the SOLID-plugin³ to detect slice-wise outliers and follow the uncertainty propagation during the subject motion- and eddy current correction.

Estimation and bootstrapping
We fitted SH and computed RISH features $$$\parallel C_i\parallel^2=\sum_{j=1}^{2i+1}C_{ij}^2$$$^9,10 on simulations and the neonatal data both with LLS and RLLS estimators¹² (eq. 2). 1000 bootstrap samples were generated from the estimates.

Results

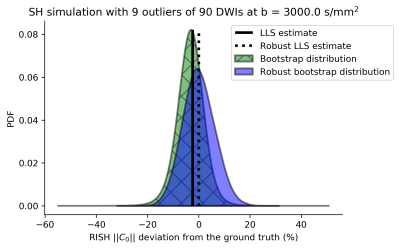
Simulations
FIG. 1 depicts a probability density function for 10% outliers demonstrating that LLS estimates and corresponding bootstraps are underestimated compared to the ground-truth. RLLS estimates and the robust bootstraps are less affected by the outliers.

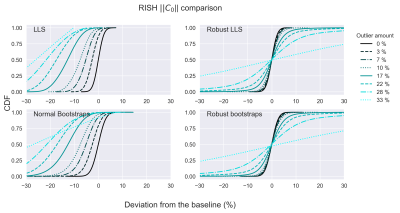
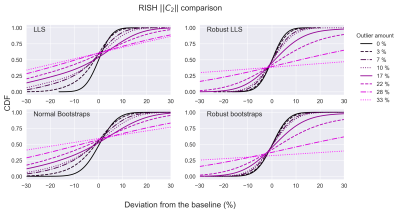
To visualize all simulations simultaneously, cumulative distribution functions (CDF) were computed (FIG. 2 and FIG. 3 for C₀ and C₂ respectively). Non-robust bootstrap/LLS CDFs of C₀ rapidly lose accuracy (CDF=0.5 deviates from x=0) with increasing outlier-fraction whereas robust bootstrap/RLLS CDFs remained accurate up to 10% of outliers. The C₂ bootstrap CDFs indicate a gradual decrease in accuracy and more rapid decrease in precision (decreasing CDF steepness) with non-robust bootstrapping/LLS whereas robust bootstrapping/RLLS CDFs remained stable up to 10% outliers.

In vivo data
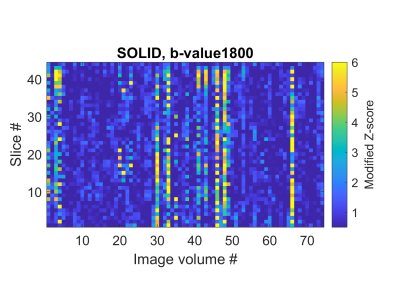
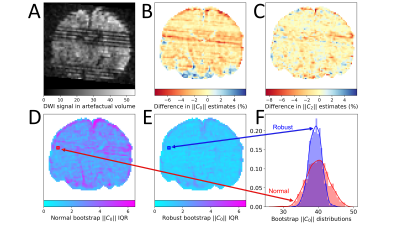
The SOLID output of the $$$b=1800\frac{\mathrm{s}}{\mathrm{mm}^2}$$$ shell used in the analysis is shown in FIG. 4 indicating several slice-wise outliers. FIG. 5 demonstrates the differences between methods, revealing that in the presence of outliers, RLLS and robust bootstrapping can still produce reliable estimates of the features and their uncertainties.

Discussion and Conclusion

We presented a novel robust residual bootstrap algorithm to evaluate the uncertainty of dMRI models and signal representations exhibiting homoscedasticity, and showcased its performance in SH and RISH estimation. Our algorithm could successfully quantify uncertainty when the number of outliers remained below 10%. Moreover, the results on a neonatal dataset demonstrated visually (FIG. 5) that the robust bootstrap distribution was less affected by outliers. In future, we aim to explore if block-bootstrapping would be beneficial in long acquisitions where resampling residuals might be biased e.g. due to signal drift.¹⁵ Our algorithm could improve the reliability of analyses that aim to study SH⁹ features, harmonize DW measurements across scanners¹⁰, or to perform probabilistic tractography².

Acknowledgements

This study was conducted using data from the Human Connectome Project (www.humanconnectome.org). VS was supported by the Brain Research Foundation Verona and the Emil Aaltonen Foundation. CMWT was supported by a Sir Henry Wellcome Fellowship (215944/Z/19/Z) and a Veni grant (17331) from the Dutch Research Council (NWO).

References

1. Harms, R. L., Fritz, F. J., Schoenmakers, S. & Roebroeck, A. Fast quantification of uncertainty in non-linear diffusion MRI models for artifact detection and more power in group studies. bioRxiv 651547 (2019). doi:10.1101/651547

2. Jeurissen, B., Leemans, A., Jones, D. K., Tournier, J. D. & Sijbers, J. Probabilistic fiber tracking using the residual bootstrap with constrained spherical deconvolution. Hum. Brain Mapp. 32, 461–479 (2011).

3. Sairanen, V., Leemans, A. & Tax, C. M. W. Fast and accurate Slicewise OutLIer Detection (SOLID) with informed model estimation for diffusion MRI data. Neuroimage 181, 331–346 (2018).

4. Tax, C. M. W., Otte, W. M., Viergever, M. A., Dijkhuizen, R. M. & Leemans, A. REKINDLE: Robust Extraction of Kurtosis INDices with Linear Estimation. Magn. Reson. Med. 73, 794–808 (2015).

5. Pannek, K., Raffelt, D., Bell, C., Mathias, J. L. & Rose, S. E. HOMOR: Higher Order Model Outlier Rejection for high b-value MR diffusion data. Neuroimage 63, 835–842 (2012).

6. Chang, L. C., Walker, L. & Pierpaoli, C. Informed RESTORE: A method for robust estimation of diffusion tensor from low redundancy datasets in the presence of physiological noise artifacts. Magn. Reson. Med. 68, 1654–1663 (2012).

7. Collier, Q., Veraart, J., Jeurissen, B., Den Dekker, A. J. & Sijbers, J. Iterative reweighted linear least squares for accurate, fast, and robust estimation of diffusion magnetic resonance parameters. Magn. Reson. Med. 73, 2174–2184 (2015).

8. Sairanen, V., Leemans, A., Jones, D. K. & Tax, C. M. W. Rebooting diffusion MRI uncertainty distributions in the presence of outliers with ROBOOT. Proc. Intl. Soc. Mag. Reson. Med. 26, 5346, 2018. ISSN: 1545-4428

9. Kazhdan, M., Funkhouser, T. & Rusinkiewicz, S. Rotation invariant spherical harmonic representation of 3D shape descriptors. Proc. 2003 … 156–165 (2003).

10. Mirzaalian, H. et al. Inter-site and inter-scanner diffusion MRI data harmonization. Neuroimage 135, 311–323 (2016).

11. Jeurissen, B., Leemans, A., Jones, D. K., Tournier, J. D. & Sijbers, J. Probabilistic fiber tracking using the residual bootstrap with constrained spherical deconvolution. Hum. Brain Mapp. 32, 461–479 (2011).

12. Veraart, J., Sijbers, J., Sunaert, S., Leemans, A. & Jeurissen, B. Weighted linear least squares estimation of diffusion MRI parameters: Strengths, limitations, and pitfalls. Neuroimage 81, 335–346 (2013).

13. Fick, R. H. J., Wassermann, D. & Deriche, R. The Dmipy Toolbox: Diffusion MRI Multi-Compartment Modeling and Microstructure Recovery Made Easy. Front. Neuroinform. 13, 64 (2019).

14. Leemans, A., Jeurissen, B., Sijbers, J. & Jones, D. ExploreDTI: a graphical toolbox for processing, analyzing, and visualizing diffusion MR data. Proc. 17th Sci. Meet. Int. Soc. Magn. Reson. Med. 17, 3537 (2009).

15. Vos, S. B. et al. The Importance of Correcting for Signal Drift in Diffusion MRI. doi:10.1002/mrm.26124

Figures

FIG. 1 An example of one noise realization with the LLS and RLLS estimates and respective probability density functions of the bootstrap samples for RISH C₀ in a setup with 10% outliers. The deviation from the ground-truth value is shown on the x-axis. RLLS is less affected by outliers as the corresponding bootstrap distribution is centered around the robust estimate whereas the LLS estimate and corresponding bootstrap distribution are both biased to underestimate C₀. However, the increased uncertainty due to outliers is seen in the wider distribution of the robust bootstrap.

FIG. 2 Cumulative distribution functions (CDF) of RISH C₀ were calculated over all 2000 noise realizations with LLS (left top), RLLS (right top) and their 1000 bootstraps on the second row. The incremental number of outliers resulted in a rapid loss of accuracy (CDF=0.5 value diverges rapidly from x=0) and more gradual loss of precision (CDF steepness decreases) of C₀ estimates with LLS estimates and their bootstrap samples. With the robust alternatives, the accuracy and precision remained stable up to 10% outliers.

FIG. 3 Cumulative distribution functions (CDF) of RISH C₂features were calculated over all 2000 noise realizations with LLS (left top), RLLS (right top) and their 1000 bootstrap samples on the second row. The incremental number of outliers resulted in a slow loose in accuracy (CDF=0.5 value remains near x=0) but rapid loose in precision (CDF losing steepness) of the C₂ features with LLS estimates and their bootstrap samples. With the robust alternatives, the accuracy and precision remained relatively intact up to 10% in outliers.

FIG. 4 Slice-wise outlier detection (SOLID) results of the neonatal data on the b=1800s/mm³ shell. Slices with modified Z-score below 3 were considered as having normal intensity variation and were not downweighted during estimation i.e. their weight was one. Slices with modified Z-scores between 3 and 6 were linearly downweighted with weights decreasing from one to zero. Measurements with modified Z-scores above 6 were completely excluded with a weight of zero.

FIG. 5 RISH-feature bootstrapping on the neonatal dataset. A DWI volume with slice-wise outliers after image registration to correct for motion. B-C Difference between LLS and RLLS estimators for the RISH features (negative colors indicate LLS < RLLS). D-E Interquartile ranges of the C₀ bootstrap samples. Slice-wise outliers are visible in D (non-robust bootstrap) but not in E (robust bootstrap). F C₀bootstrap distributions of one voxel in an outlier slice demonstrating a narrower distribution using robust bootstrapping.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

4284