4283
Blurred streamlines: a new concept to improve tractography accuracy by spatially blurring signal contributions
Alessandro Daducci1, Francesco Gobbi1, Nicola Febbrari1, Matteo Battocchio1, and Simona Schiavi1
1University of Verona, Verona, Italy
1University of Verona, Verona, Italy
Synopsis
Tractography is a powerful tool to study brain connectivity but it suffers from an intrinsic trade-off between sensitivity and specificity. The former can be increased by constructing more streamlines, while filtering techniques can improve the latter. However, creating many streamlines may introduce redundancy in the tractograms and negatively affect the performances of filtering methods, especially those based on linear optimization. Here, we present the “blurred streamlines”, a novel concept based on a combination of streamline clustering and spatial blurring of their signal contributions. Preliminary results show the potential of this formulation and open new perspectives for improving tractography accuracy.
Introduction
Tractography represents an invaluable tool in neuroscience as it allows studying brain connectivity in vivo. However, to achieve high sensitivity a large number of streamlines is required which also introduces many false positives1. To address this problem, microstructure informed tractography methods have been proposed2-7. They combine the tractogram with signal forward-models to infer the individual contributions of each streamline and filter out those not supported by the data. The Convex Optimization Modeling for Microstructure Informed Tractography (COMMIT)6 achieves this by solving the linear system: $$\operatorname{argmin}\;||\boldsymbol{A}\boldsymbol{x}-\boldsymbol{y}||_2^2\;\;\text{s.t.}\;\boldsymbol{x}\ge0$$ where the signal contributions of streamlines are encoded as separate columns of $$$\boldsymbol{A}$$$ (Fig. 1). Consequently, if some streamlines follow similar trajectories, they become redundant for explaining the data and the corresponding columns tend to become linearly dependent, making it difficult to interpret the estimated contributions $$$\boldsymbol{x}$$$. To prevent the onset of collinearity8, we introduce the novel concept of “blurred streamlines”.Methods
The proposed method is shown in Fig. 2. Given a tractogram, we first cluster its streamlines to minimize the redundancy between them, and then we spatially blur the signal contributions of the resulting centroids to guarantee coverage of all voxels. A streamline usually contributes to the signal only in those voxels it passes through (Fig. 3A,left); the terms blurred streamlines and blurred signal contributions mean that a streamline can instead contribute also to adjacent voxels and capture the uncertainty of fiber trajectories estimated through tractography (Fig. 3A,right).The procedure to achieve this is illustrated in Fig. 3B-C and is based on the Frenet-Serret frames9,10. For each centroid streamline $$$C$$$ we create replicas of $$$C$$$ by sweeping a series of $$$N$$$ circles with radii $$$r\in\{r_1,\ldots,r_N\}$$$ along its path (Fig. 3B). All circles lie on a plane that is always orthogonal to $$$C$$$ throughout the sweep and are subdivided into $$$M$$$ sectors separated by an angle $$$\alpha=2\pi/M$$$. Each circle defines exactly $$$M$$$ copies of $$$C$$$, one per sector, which are obtained by radially displacing all points of $$$C$$$ from their initial position to a distance $$$r$$$ and rotating them by an angle $$$k\alpha$$$, with $$$k\in\{1,\ldots,M\}$$$, about the center. The signal contributions of a replica are computed as usual, i.e., considering only the traversed voxels, and the total signal contributions corresponding to a centroid are obtained by summing those of all its replicas. However, the signal contributions of all replicas at radius $$$r$$$ are scaled, as function of $$$r$$$, according to a Gaussian distribution centered on $$$C$$$ with standard deviation $$$\sigma$$$ (Fig. 3C). Therefore, the blurred signal contributions of a centroid $$$C_i$$$, which form the $$$i$$$-th column of $$$\boldsymbol{A}$$$, are defined as: $$\boldsymbol{A_i}=\sum_{j=1}^N w(r_j) \sum_{k=1}^M S(C_i,r_j,\alpha_k)$$ where $$$\alpha_k=2\pi k/M$$$ and $$$S(C_i,r_j,\alpha_k)$$$ are the signal contributions of the replica of $$$C_i$$$ at radius $$$r_j$$$ and sector $$$\alpha_k$$$, which are then scaled by the factor $$$w(r_j)=\exp({-0.5\,r_j^2/\sigma^2})$$$.
We evaluated the efficacy of blurred streamlines on a well-known synthetic phantom as in7, which consists of 27 bundles between 53 gray-matter regions mimicking realistic fiber configurations of the brain (Fig. 4A). We generated 1 million streamlines using both deterministic and probabilistic algorithms of MRtrix311, discarding those ending prematurely in white matter. Finally, we used QuickBundles12 with the Average of Pointwise Euclidean Metric to cluster the streamlines.
Results and Discussion
Fig. 4 analyzes the behavior of our new formulation when varying the extent of clustering and blurring; plots correspond to deterministic tracking, which contained 273 invalid bundles (IB), but similar results were obtained for probabilistic. Standard COMMIT (i.e., no clustering) reduced the IB by ≈17% (273→226) without losing valid bundles (VB), but a much higher percentage of IB can be removed with blurred streamlines (≈71%, 273→80). As the blur radius increases more IB are filtered out, but an excessive blur may lead to losing VB, although only marginally (Fig. 4B). Fig. 4C shows that increasing the blur requires more computation time (6’→1h20’) and RAM (377MB→6.5GB). Nonetheless, clustering can reduce significantly the tractogram size (Fig. 4C,left) and, thus, alleviates the computational demands of our method. Fig. 5 visually compares the connectomes estimated using COMMIT, both deterministic and probabilistic cases, with and without blurred streamlines, but using the same computational resources.We point out that a direct approach to reduce redundancy by removing linearly dependent columns from $$$\boldsymbol{A}$$$ is impractical due to the size of the data, i.e., millions of streamlines, thousands of voxels, and several dMRI measurements. Our preliminary results show the effectiveness of our heuristic solution, which also helps to improve the accuracy of reconstructions. Future work will be necessary to confirm its validity in the case of real brain data, as well as its benefits in combination with COMMIT27. Finally, we investigated the effects of blurred streamlines using COMMIT; however, since other filtering procedures3-7 might suffer from redundancy in the tractograms, blurred streamlines may have positive effects also for such methods.
Conclusions
We called attention to the presence of redundancy in tractography and the possible ramifications it may have on the accuracy of the reconstructions when using filtering techniques based on linear formulations. To mitigate this problem, we introduced a novel way to define how streamlines contribute to the signal. Our results suggest that this new formulation represents an effective solution towards more accurate tractography reconstructions.Acknowledgements
Alessandro Daducci was supported by the Rita Levi Montalcini Programme for young researchers of the Italian Ministry of Education, University and Research. The authors would like to thank Filippo Baccaglini and Valentina Nale (M.Sc. students at the University of Verona) for their help during the initial stages of the project.References
- K. Maier-Hein et al., “The challenge of mapping the human connectome based on diffusion tractography,” Nat Commun, vol. 8, pp. 1349, 2017
- A. Daducci, A. Dal Palú, M. Descoteaux, J.-P. Thiran, “Microstructure informed tractography: Pitfalls and open challenges,” Front Neurosci, vol. 10, pp. 247, 2016
- R. Smith, J.-D. Tournier, F. Calamante, A. Connelly, “SIFT: spherical-deconvolution informed filtering of tractograms,” Neuroimage, pp. 298–312, 2013
- R. Smith, J.-D. Tournier, F. Calamante, A. Connelly, “SIFT2: Enabling dense quantitative assessment of brain white matter connectivity using streamlines tractography,” NeuroImage, vol. 119, pp. 338–51, 2015
- F. Pestilli, J. Yeatman, A. Rokem, K. Kay, B. Wandell, “Evaluation and statistical inference for human connectomes,” Nat Methods, pp. 1058–63, 2014
- A. Daducci, A. Dal Palù, A. Lemkaddem, J.-P. Thiran, "COMMIT: Convex Optimization Modeling for Microstructure Informed Tractography," IEEE Trans Med Imaging, vol. 34, no. 1, pp. 246-57, 2015
- S. Schiavi, M. Ocampo-Pineda, M. Barakovic, L. Petit, M. Descoteaux, J.-P. Thiran, A. Daducci, "A new method for accurate in vivo mapping of human brain connections using microstructural and anatomical information," Sci Adv, vol. 6, no. 31, pp. eaba8245, 2020
- D. A. Belsley, E. Kuh, R.E.Welsch, Regression diagnostics: identifying influential data and sources of collinearity, New York (N.Y.) : Wiley, 1980
- J. A. Serret, "Sur quelques formules relatives à la théorie des courbes à double courbure," J Math Pures Appl, pp. 193-207, 1851
- J. F. Frenet, "Sur les courbes à double courbure," J Math Pures Appl, pp. 437-47, 1852
- J.-D. Tournier, R. Smith, D. Raffelt, R. Tabbara, T. Dhollander, M. Pietsch, D. Christiaens, B. Jeurissen, C.-H. Yeh, A. Connelly, "MRtrix3: A fast, flexible and open software framework for medical image processing and visualisation," Neuroimage, vol. 202, pp. 116-37, 2019
- E. Garyfallidis, M. Brett, M. Correia, G. Williams, I. Nimmo-Smith, "Quickbundles, a method for tractography simplification," Front Neurosci, vol. 6, pp. 175, 2012
Figures
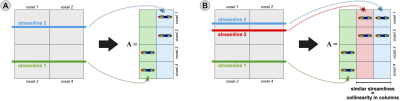
Fig. 1. The problem addressed in this work. When streamlines follow similar trajectories, the corresponding columns in matrix A tend to become linearly dependent, posing serious concerns for the interpretation of the estimated coefficients.
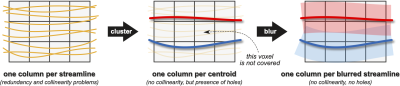
Fig. 2. Our solution consists of two steps. First, we cluster the input streamlines (left, yellow) to minimize the redundancy between them. The resulting centroids (middle, red and blue streamlines) are, by construction, sufficiently dissimilar and likely generate non-collinear columns in A. However, the simplified tractogram with only these centroids may not cover properly all voxels. Thus, we spatially blur their signal contributions (right, transparent areas) to guarantee proper coverage.

Fig. 3. Blurred streamlines. A streamline contributes to the signal only in those voxels it passes through, whereas a blurred streamline can contribute also to adjacent voxels. The signal contributions decrease as function of the distance r and according to a Gaussian distribution with standard deviation σ centered on the streamline itself.
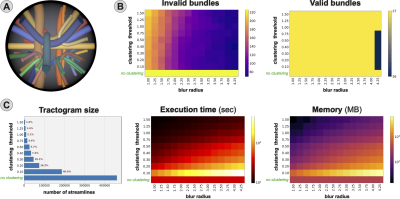
Fig. 4. Characterization of the behavior of the blurred streamlines formulation when varying the extent of the clustering (clustering threshold) as well as of the blur (blur radius). In simulated data with known ground truth, we evaluated the number of valid bundles (VB) and invalid bundles (IB), the size of the clustered tractogram as well as the required computational resources (execution time and RAM). Plots correspond to deterministic tractography.
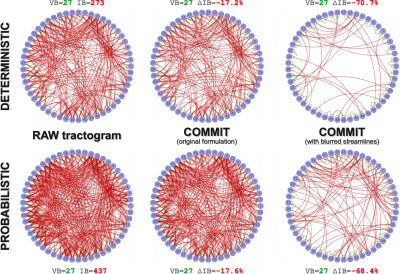
Fig. 5. Quantitative comparison of the performance of COMMIT without and with blurred streamlines. ΔIB is the reduction (in percentage) of the IB with respect to the raw tractogram. Green and red arcs represent the reconstructed VB and IB between the 53 gray-matter regions (blue nodes). For both deterministic and probabilistic cases, the standard COMMIT can reduce the number of IB by ≈17%, whereas the introduction of blurred streamlines enables a much higher percentage of reduction (≈70%).