4269
Real-time electric field estimation in transcranial magnetic stimulation using deep learning and magnetic resonance imaging1Wuhan Institute of Technology, Wuhan, China, 2Brigham and Women's Hospital, Boston, MA, United States, 3Harvard Medical School, Boston, MA, United States, 4Massachusetts General Hospital, Boston, MA, United States
Synopsis
Transcranial magnetic stimulation (TMS) is an effective treatment approach for mental disorders. Accurate and rapid prediction of TMS-evoked electric field (E-field) in brain tissue is important for accurate targeting and to understand the mechanism of treatment response. The standard method for E-field prediction is based on physical modeling which usually takes long computational time. In this work, we introduce a method based on deep neural networks (DNNs) for real-time E-field prediction. We show that the trained DNN can predict high-precision whole-brain E-field in 0.24 seconds. Moreover, diffusion-MRI based tissue conductivity tensor can improve the prediction accuracy of E-field.
Introduction
Transcranial magnetic stimulation (TMS) is a non-invasive neuromodulation technique that has been used to treat patients with mental disorders such as major depressive disorder (MDD), obsessive-compulsive disorder and also used in basic neuroscience research1. In TMS, a magnetic coil with oscillating current is placed near the scalp to generate electric field (E-field) in brain tissue in order to modulate neural activity in a target brain region2. However, due to the complex geometry and tissue structure of the brain, such as the skull thickness, the electrical conductivity variation across different tissues, the maximal stimulation strength of E-field does not always happen at the expected location3 and the stimulated brain target is not straightforward to identify4. Thus, it is necessary to accurately estimate the distribution of electric field (E-field) induced in the brain to improve brain targeting in TMS5. Numerical computations, which is based on the finite element method, have been used to estimate the stimulated electric field (E-field) by TMS in brain tissue. But the relatively long computation time limits the real-time application of this approach. The goal of this work is to integrate the deep learning technique with subject-specific magnetic resonance imaging (MRI) data to accelerate the prediction of E-field.Method
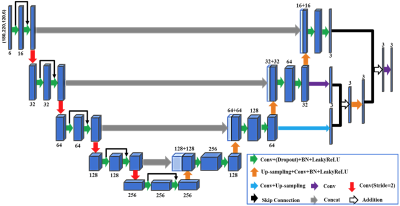
We propose a deep neural network (DNN) that uses MRI data and the magnetic field of TMS coil to predict the E-field. The architecture of the proposed DNN is illustrated in Fig. 1 which integrates the 3D U-net architecture, residual modules and a mechanism to combine multi-scale features maps and is referred to as 3D-MSResUnet. The input data of the DNN includes the principal tissue conductivity vector estimated using subject-specific diffusion MRI (dMRI) and T1w MRI5 and the magnetic field of the TMS coil. The diffusion tensors estimated using dMRI can improve the accuracy of the estimated E-field. To examine the advantage of using dMRI in the proposed method, we also trained another DNN with the same architecture, but the input data only includes the T1w MRI and the magnetic field of the TMS coil. We note that a DNN based method has been proposed in6 which uses the standard U-net and T1w MRI to predict the E-field. Our method uses a novel DNN architecture, dMRI based tissue conductivity and the coil magnetic field, which is unique to our method compared to previous works.We trained the DNN using simulation data based on 60 subjects from the Human Connectome Project. The reference E-field maps were simulated using the SimNIBS toolbox5 based on the Magstim 70 mm Figure-of-Eight TMS coil7. Each subject had 4056 simulated E-field volumes that were obtained with 52 TMS coil positions and 78 coil direction at each position. Then, we tested the trained DNN using data from another 5 subjects that were not used in the training. We evaluated the correlation coefficient, angular difference between the DNN-predicted and the reference E-field. Moreover, we computed the distance between the peak magnitude of the E-field maps to evaluate the difference in targeting accuracy. The performance of the DNN of was not only examined at the coil positions that were used in the training but also any positions that were not trained.
Results
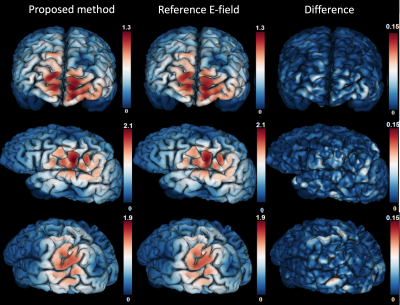
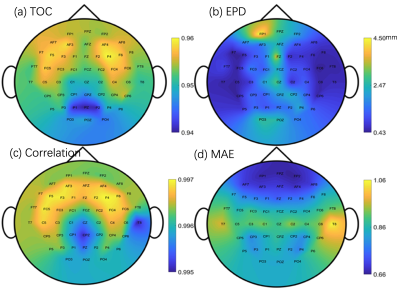
All the evaluation metrics showed that the DNN-predicted E-field maps were similar to the FEM-based reference with arbitrary coil positions and orientations. Fig. 2 illustrates the magnitude of the predicted E-field using the proposed method and the reference and their differences at a fixed coil position. Fig. 3 illustrates the spatial distribution of the several evaluation metrics, including (a) the overlapping coefficient of the surface area with top 5% magnitude of E-field, i.e. target overlapping coefficient, (b) E-field peak distance, (c) E-filed correlation coefficient, (d) maximum absolute error, between DNN-predicted and reference E-field with coil placed at different positions. In particular, the average overlap ratio of the target regions, i.e. the target overlapping coefficient was 96.2% and the correlation coefficient of the E-field was 99.7%. Moreover, the average distance between the locations of the peak values as predicted by the proposed method and the true E-field was only about 1.3 mm, indicating the proposed approach provided high accuracy for TMS targeting. Furthermore, the angular differences between the predicted E-field with anisotropic conductivity tensor and the ground truth was about 9 degrees, which is much lower than the 13-degree angular error using only T1w images (without anisotropic conductivity tensors). Finally, the prediction time for a whole-brain three-dimensional E-field was about 0.24 seconds, which is much shorter than the computational time of the standard FEM approach which is about 5 – 10 minutes. The rich information provided by our approach and the ultra-short computational time makes it suitable to be applied in clinical settings.Conclusion
Our results have shown that deep learning is a promising technique for real-time E-field prediction in TMS. Real-time E-field prediction can significantly improve the targeting accuracy that is help of improve treatment efficacy and to understand the mechanism of treatment response. Thus, the proposed deep learning and MRI based method can improve the treatment of MDD, OCD and other brain disorder.Acknowledgements
This work was supported in part by NIH grants K01MH117346 (LN), R21MH116352 (LN), R21MH115280 (LN and JC). XG was supported by Graduate School of Huazhong University of Science and Technology. This study was completed while XG visited the Psychiatry Neuroimaging Laboratory at Brigham and Women’s Hospital in 2019. The authors would like to thank Fan Zhang and Joshua Goldenberg for their helpful assistance.References
[1] Rossi S, Hallett M, Rossini PM, Pascual-Leone A, Group S of TMSC. Safety, ethical considerations, and application guidelines for the use of transcranial magnetic stimulation in clinical practice and research. Clin Neurophysiol 2009;120:2008–39.
[2] Saturnino GB, Madsen KH, Thielscher A. Efficient Electric Field Simulations for Transcranial Brain Stimulation. BioRxiv 2019:541409.
[3] Bungert A, Antunes A, Espenhahn S, Thielscher A. Where does TMS stimulate the motor cortex? Combining electrophysiological measurements and realistic field estimates to reveal the affected cortex position. Cereb Cortex 2016;27:5083–94.
[4] Bakir AA, Bai S, Lovell NH, Martin D, Loo C, Dokos S. Finite Element Modelling Framework for Electroconvulsive Therapy and Other Transcranial Stimulations. Brain Hum. Body Model., Springer; 2019, p. 27–47.
[5] Saturnino GB, Thielscher A, Madsen KH, Knösche TR, Weise K. A principled approach to conductivity uncertainty analysis in electric field calculations. Neuroimage 2019;188:821–34.
[6] Yokota T, Maki T, Nagata T, Murakami T, Ugawa Y, Laakso I, et al. Real-Time Estimation of Electric Fields Induced by Transcranial Magnetic Stimulation with Deep Neural Networks. Brain Stimul 2019;12:1500–7.
[7] Thielscher A, Kammer T, Electric field properties of two commercial figure-8 coils in TMS: calculation of focality and efficiency. Clin Neurophysiol 2004; 115:1697–1708.
Figures