4255
Joint Radial Trajectory Correction for Fast T2* Mapping on an MR-Linac1Joint Department of Physics, The Institute of Cancer Research, London, United Kingdom, 2The Royal Marsden NHS Foundation Trust, London, United Kingdom, 3Computer Science Department, The University of Bath, Bath, United Kingdom
Synopsis
Measuring T2* relaxation during the course of MR-guided radiotherapy can characterize tumour hypoxia, which is associated with treatment resistance. T2* mapping with radial trajectories allows for efficient coverage of k-space but is susceptible to errors arising from gradient delays. We propose a method that jointly estimates gradient delays and T2* using model-based reconstruction. Using the numerical phantom and the in-vivo prostate data we demonstrated that the proposed approach performs better for different noise levels for both fully sampled and undersampled datasets. This will allow better integration of T2* mapping for hypoxia imaging into an MR-linac treatment work flow.
Background
T2* mapping can be a potential biomarker to characterize hypoxia and monitor treatment response throughout the course of MR-guided radiotherapy on an MR-Linac1. However, implementing a T2* mapping sequence that is robust, immune to system imperfections, and has acceptable acquisition time is challenging. T2* mapping with radial sampling allows for better coverage of k-space and is less sensitive to motion and flow artifacts. However, radial trajectories are susceptible to errors arising from gradient delays and short‐term eddy currents. Several approaches have been proposed in the past to correct for deviations of the gradient waveform. These include methods that require separate calibration scans2, special hardware to monitor the gradient field3 and calibration-less methods that jointly estimate images, and gradient delays4,5. We proposed a joint gradient delay and T2* estimation from an undersampled golden angle radial stack-of-stars trajectory for MR-guided radiotherapy on an MR-Linac.Theory
The proposed approach combines Trajectory Auto-Corrected Image Reconstruction (TrACR)4 with model-based reconstruction6 of the T2* maps. The k‐space trajectory errors are modeled as a sum of weighted error basis functions and the cost function is optimized using a conjugate gradient algorithm. The proposed approach extends this cost function to include the physical model of T2* relaxation and regularise the cost function with the model consistency term:$$ \operatorname*{arg\,min}_{∆t_k,T2^*,M_0,x_n}∑_n^N∑_c^C\parallel F({\triangle t_k})S_c x_n-y_{n,c}\parallel^2+ λ_1\parallel x_n - M_0 exp(-TE_n/(T2^*)\parallel ^2 $$
Here $$$x_n$$$ is the series of images (n = 1, …, N, and N the number of echoes),$$$ F({\triangle t_k})$$$ is a multichannel non‐uniform fast Fourier transform (NUFFT) operator parameterized by k‐space shifts caused by the delays $$$\triangle t_k$$$ for every $$$k$$$ location, $$$S_c$$$represents the coil sensitivity maps (with c = 1,…, C, and C the number of coils) and $$$\lambda$$$ is the regulariser weight. The cost function in the above equation is optimized using alternating minimization which alternates between minimizing the objective function and imposing model-consistency. First, we fix the gradient delay $$$\triangle t_k$$$ and solve for the coil images $$$x_n$$$. After solving for the $$$x_n$$$, $$$ \triangle t_k$$$ is approximately solved using nonlinear Polak–Ribière CG algorithm as described in (6). The gradient timing delay $$$\triangle t_k$$$can then be used to update k‐space coordinates for the next iteration.
Materials and Methods
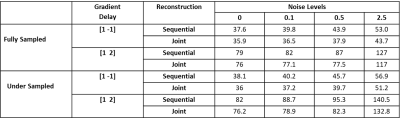
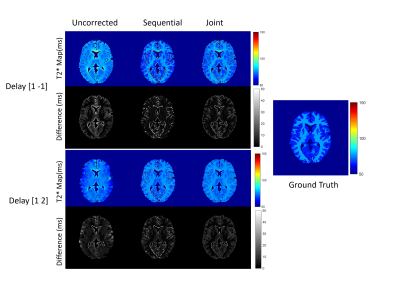
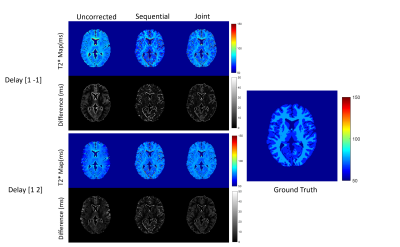
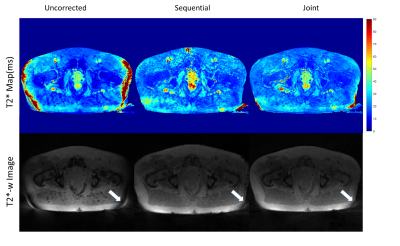
To validate the algorithm, numerical simulations were performed based on a 256 × 256 brain image7 with T2* relaxation maps. Multi-echo T2*-weighted images were calculated using simulated coil sensitivity profiles for 8 channels. The simulation was performed using a golden angle radial k-space trajectory with 512 spokes and 402 readout points. Gradient delays were simulated for x and y gradient coils separately ([1,-1] and [1, 2] in units of the sampling time), to generate corrupted k‐space data as described5. Complex Gaussian noise was added to the raw k-space data with varying noise levels (0, 0.1, 0.5, and 2.5). The dataset was undersampled retrospectively and spokes were removed from the start of the acquisition of each echo. T2* maps were estimated using the proposed approach where gradient delay correction and T2* estimation were performed jointly and the sequential approach where T2* estimation was performed after the gradient delay correction. Root mean squared error (RMSE) was calculated from the reconstructed and the ground truth T2* maps for fully sampled and undersampled dataset. In-vivo data were collected in five prostate patients undergoing radiotherapy on a 1.5 T MR- Linac (Elekta AB. Stockholm, Sweden) using a radial stack-of-stars spoiled multi-gradient echo sequence8 with the following parameters (8 echoes, 269 spokes, TR = 48 ms, ΔTE=5ms, FOV = 400x400x180 mm and 1.5x1.5x6 mm3 acquisition voxel size). The acquisition time for the fully sampled scan was 7:56 min. The data was reconstructed and corrected for the gradient delays using the joint and sequential approach as described above.Results
Numerical simulations demonstrated that for both the fully sampled and undersampled dataset, the joint estimation performed better than the sequential approach. Table 1 compares the RMSEs for the numerical phantom for both the undersampled and fully sampled datasets. As expected, the RMSEs increased as the level of noise increased in all the cases. Overall, the RMSEs for the gradient delay [1, -1] was less than for the gradient delay [1, 2]. T2* maps reconstructed without correction, joint and sequential approach are shown in Figure 2 for fully sampled data and Figure 3 for undersampled data. The corresponding difference maps reveal that the joint reconstruction resulted in less error as compared to the sequential approach. Similar results were observed in the in-vivo data (Figure 4) where T2* maps reconstructed with the proposed approach showed better T2* estimation as compared to the sequential reconstruction.Discussion and Conclusion
This is a proof-of-concept study exploring the correction of radial k-space trajectories for T2* mapping. We find that a joint correction and model-based reconstruction improved the quality of T2* parameter maps for fully and undersampled data sets. The reconstruction from undersampled data could be improved further by varying the angular sampling pattern for different echo times. These will be explored in future work, which will also focus on fast computation methods to facilitate implementation into the clinical workflow on the MR-Linac.Acknowledgements
No acknowledgement found.References
1. Panek R, Welsh L, Baker LC, Schmidt MA, Wong KH, Riddell AM, et al. Noninvasive imaging of cycling hypoxia in head and neck cancer using intrinsic susceptibility MRI. Clinical Cancer Research. 2017;23(15):4233-41.
2. Duyn JH, Yang Y, Frank JA, van der Veen JW. Simple correction method for k-space trajectory deviations in MRI. Journal of Magnetic Resonance. 1998;132(1):150-3.
3. Barmet C, Zanche ND, Pruessmann KP. Spatiotemporal magnetic field monitoring for MR. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine. 2008;60(1):187-97.
4. Ianni JD, Grissom WA. Trajectory auto‐corrected image reconstruction. Magnetic resonance in medicine. 2016;76(3):757-68.
5. Jiang W, Larson PE, Lustig M. Simultaneous auto‐calibration and gradient delays estimation (SAGE) in non‐Cartesian parallel MRI using low‐rank constraints. Magnetic resonance in medicine. 2018;80(5):2006-16.
6. Bano W, Golbabaee M, Benjamin A, Marshall I, Davies M, editors. Improved Accuracy of Accelerated 3D T2* Mapping through Coherent Parallel Maximum Likelihood Estimation. Proceedings of the Joint Annual Meeting ISMRM-ESMRMB, Paris, France; 2018.
7. Collins DL, Zijdenbos AP, Kollokian V, Sled JG, Kabani NJ, Holmes CJ, Evans AC. Design and construction of a realistic digital brain phantom. IEEE transactions on medical imaging. 1998 Jun;17(3):463-8.
8. Block KT, Chandarana H, Milla S, Bruno M, Mulholland T, Fatterpekar G, et al. Towards routine clinical use of radial stack-of-stars 3D gradient-echo sequences for reducing motion sensitivity. Journal of the Korean Society of Magnetic Resonance in Medicine. 2014;18(2):87-106.
Figures