Introduction

Imaging simulation, is an essential step of radiation treatment planning. For better delineation of the target and organs-at-risk (OARs), MR has increasingly been adopted as a simulation platform complementary to CT. Despite demonstrated successes in many other disease sites, MR simulation is challenging in the mobile abdominal site because 1) multi-contrast images (useful for differentiating multiple OARs or the target) are typically acquired in separate scans with unmatched parameters or varied motion compensation strategies, and are susceptible to inter-scan misalignment; 2) image quality of breath-hold scans can be severely degraded in patients with poor compliance or limited breath-hold capacity; 3) existing 4D MR (i.e. motion resolved volumetric imaging for better understanding of target motion) techniques are all limited to a single contrast weighting ^1-4, which may be suboptimal for target delineation. In this work, we present a standalone MR simulation technique that accomplishes multiple tasks: to provide multiple, dynamic contrast weightings with inherent spatial co-registration and to provide motion-resolved volumetric images.

Method

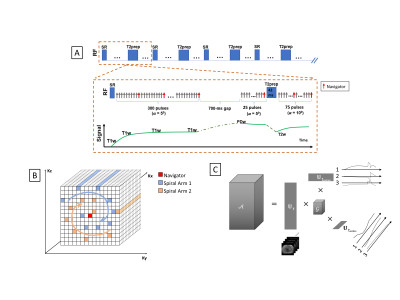
Sequence Design:
As shown in Fig. 1, each repetition time (TR) of our multi-task (MT) MR sequence starts with a saturation recovery (SR) pulse followed by a group of FLASH readouts during T1 recovery, a short temporal gap, and a second and third group of FLASH readouts before and after T2-preparation, respectively. K-space is sampled with a Cartesian spiral-in pattern (Fig. 1B) with 10 lines in each spiral arm and the 10th line being the k-space center and used as the navigator. This sampling pattern allows for 1) a more densely sampled k-space center region but faster reconstruction time compared to radial sampling and 2) reduced eddy current effects and thus high-quality navigator and images due to smaller k-space jumps when the k-space center is sampled ^5,6.

Image reconstruction framework:
Using MR Multitasking⁷ (MT), a low-rank tensor (LRT) technique, we can efficiently encode an image function of these multiple MR spatiotemporal dimensions (i.e. physical dimensions, motion, contrast) into linear combinations of the spatial coefficients $$$\mathbf{U}_\mathbf{r}$$$ , as shown in fig. 1C. In this case, $$ \mathcal{A}\ =\mathcal{G}\ \times_1\mathbf{U}_\mathbf{r}\times_2\mathbf{U}_{motion}\times_3\mathbf{U}_{contrast}$$
Where $$$\mathcal{A}$$$ is the tensor representing a multidimensional image A(r,$$$t_{motion}$$$, $$$t_{contrast}$$$) with r being the physical dimensions [x,y,z], and $$$t_{motion}$$$, $$$t_{contrast}$$$ being the temporal dimensions. The $$$\mathbf{U}$$$ matrices contain basis functions for each dimension, and $$$\mathcal{G}$$$ is the core tensor. A combined temporal factor $$$\mathrm{\Phi}=\mathcal{G}\times_2\mathbf{U}_{motion}\times_3\mathbf{U}_{contrast}$$$ is determined from Bloch-constrained low-rank tensor completion and motion binning from the navigator data. We then determine $$$\mathbf{U}_\mathbf{r}$$$ by$$
\hat{\mathbf{U}}_\mathbf{r} = \underset{\mathbf{U}_\mathbf{r}}{\arg\min} \|d-\Omega(\Phi \times_1 E \mathbf{U}_\mathbf{r})\|^2_2
$$
where $$$\mathbf{d}$$$ contains the measured imaging data, $$$\Omega$$$ is the spiral-in Cartesian sampling operator, $$$\mathbf{E}$$$ is the multi-channel spatial encoding operator, and $$$\lambda$$$ is the Lagrange multiplier for $$$R\left(\mathbf{U}_\mathbf{r}\right)$$$, a wavelet regularizer.

Experiments:
The MT-MR sequence was evaluated through in-silico and in-vivo experiments, using following imaging parameters: coronal orientation, FOV = 256(SI) x 358(LR) x 256(AP) mm³, resolution = 1.6 x 1.6 x 3.2(interpolated to 1.6) mm³, echo spacing/TE = 6/2.62 ms, gap time = 700ms, total scan time = 9:30min. 3D images were reconstructed with 8 motion phases.
We first simulated the sequence using the digital abdomen motion phantom developed by Lo et al.^8,9 The quality of reconstructed images were evaluated against the “digital truth” of the phantom by 1) visually comparing contrast weightings and liver dome’s locations at motion state 1 and 8 and 2) calculating structural similarity (SSIM) maps (structural component) between MT-MR images and the ground truth at motion state 8 (end-exhalation).
We also performed testing on 6 healthy volunteers on a 3T system (MAGNETOM Vida, Siemens Healthcare, Erlangen, Germany). During the scan, volunteers were instructed to lie still and breathe normally. Repeated free-breathing MR images (>1 fps) of a 2D coronal slice were acquired to provide motion references in 3 subjects. The ranges of respiratory motion measured at the liver dome were compared between MT-MR and the reference method.

Results

In silico
Fig. 2 shows the reconstructed results from the digital phantom simulations at motion state 1 and 8 across 3 contrast points, along with their respective digital truth. MT-MR provided visually comparable contrast weightings and liver locations when compared to the digital truths. The structural SSIM maps show that our reconstruction algorithm was successful in recovering the majority of anatomical structures, although most structural differences occur at organ boundaries, likely due to edge blurring.

In vivo
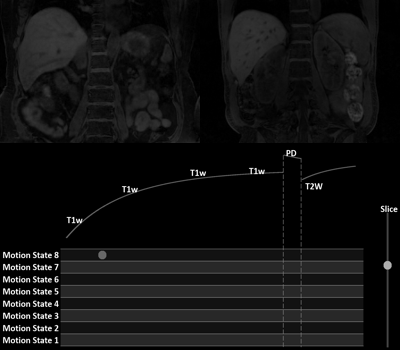
Fig. 3 showcases the capabilities of our MT-MR technique. One may visualize abdominal structures in a flexible fashion because of the availability of volumetric, motion-resolved, multi-contrast images. The differences in motion ranges of the liver dome between MT-MR and 2D references were within 0.2 mm (Fig. 4A). Fig. 4B shows the matched liver locations from volunteer 1 between MT-MR and the 2D reference images.

Discussion

In this work, we developed an MT-MR simulation technique that provides respiratory motion-resolved, spatially co-registered multi-contrast, and volumetric MR images for abdominal radiation treatment planning. Its technical feasibility was demonstrated on a digital phantom and healthy volunteers. There is still room to further improve spatial resolution. More importantly, the technique needs to be validated in patients receiving radiation therapy. In conclusion, MT-MR is technically feasible in serving MR simulation in abdominal radiation treatment planning.

Acknowledgements

This work is supported by NIH grant NIH/NIBIB R01EB029088