Synopsis

MR-linac systems allow for real-time tumor position updates. Higher temporal resolution imaging through k-space undersampling allows for an increased number of position updates, however iterative reconstructions may negate the decrease in acquisition time and undersampling artifacts may impact tracking stability.

In this study a fast method to denoise and suppress image artifact using a U-net is presented. Undersampled Cartesian and radial cine images were acquired from a patient with a liver tumor on an MR-linac. Tumor tracking stability was assessed. Denoising was found to improve tracking stability and has potential in high temporal resolution cine imaging on MR-linac systems.

Introduction

Hybrid MR-linac systems allow for the direct tumor visualization using real-time cine MRI during radiotherapy. Tumor motion can be compensated for by tracking the tumor contour and gating radiation delivery when the tumor moves out of the target region. For this purpose fast imaging in combination with robust tumor tracking is essential. Faster image acquisition can be achieved through sub-Nyquist sampling of k-space data, however this can lead to prolonged reconstruction times which is unsuitable for real-time tracking. In this work, the temporal resolution of a cine sequence is increased by undersampling radial and Cartesian acquisitions. To compensate for the resultant undersampling artifacts, a U-net was used for denoising. In addition, a second U-net was employed for tumor tracking.

Methods

All images were acquired on a low-field MR-linac (MRIdian Linac System, ViewRay Inc., Cleveland, Ohio, USA). One healthy volunteer was measured in order to optimize network parameters as well as one patient undergoing treatment for liver cancer for which the denoising method could be tested and tracking performance evaluated.

A bSSFP sequence was implemented to maximize signal-to-noise ratio [1] with the following parameters: voxel size = 2.3x2.3x7.5 mm³, field of view = 300x300 mm², TR/TE = 3.14 ms / 1.57 ms, flip angle = 90°. Both radial and Cartesian k-space read-out schemes were implemented. Radial scheme used the 10th tiny golden angle increment between spokes [2], and were reconstructed using both an adjoint NUFFT [3] as well as iterative SENSE [4]. Undersampled Cartesian images were reconstructed by a zero-filled inverse FFT as well as GRAPPA [5] using five calibration lines.

All reconstructions were performed with varying undersampling factors, performed retrospectively, in order to assess image quality. Images were reconstructed using 128 k-space lines (reference images, 2.5 fps), 30 lines (10.6 fps), 20 lines (15.9 fps) and 10 lines (31.8 fps) for both Cartesian and radial data. From the reference images, 50 tumor contours were manually created. A 5-fold cross-validation was used to analyze 200 images in total.

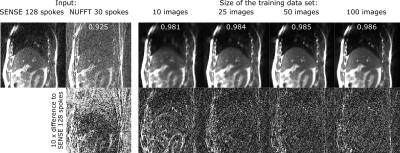
Denoising of undersampled radial and Cartesian images was performed using a neural network with the U-net architecture [6]. The U-net was trained over 100 epochs with 50 pairs of images: one image with 128 spokes and lines, respectively, and the corresponding undersampled image.

The tumor was tracked in the images with and without denoising using a second U-net network with the same architecture. This U-net was trained with image augmentation over 150 epochs with 10 images and their manual tumor contours.

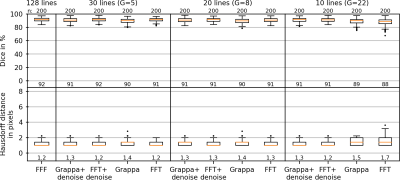
Images were compared to the reference images quantitatively using a normalized cross-correlation. The tracking was evaluated using two metrics: dice coefficient and the Hausdorff distance.

Results

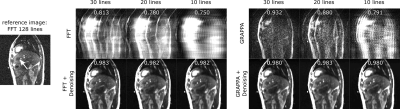
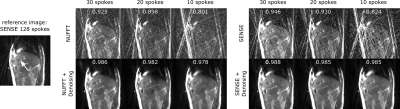
Denoising performance increased with the size of the training data set (Fig. 1). Using 10 training images was sufficient to increase image quality and suppress noise and streaking artifacts, however significant blurring occurred. With 50 training images, blurring is reduced such that vessels within the liver are clearly visible.

On a visual inspection of the images (Fig. 2), it can be seen that denoising strongly improves image appearance compared to images reconstructed with inverse FFT or GRAPPA, even in the case of high undersampling factors. This is also demonstrated quantitatively, on observation of the normalized cross-correlation values. For radial images (Fig. 3), denoising is also highly effective and a similar trend to that of the Cartesian images can be observed.

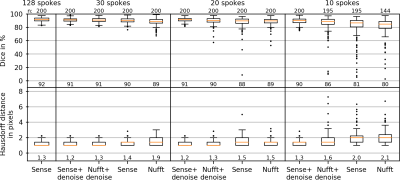
Tracking metrics are shown in Figs. 4 and 5 for Cartesian and radial image data. It can be seen that for highly undersampled data, image denoising improved tracking stability. In this case, Cartesian-acquired images can be seen to have improved tracking metrics compared to radially-acquired images.

Discussion

In this study, the Cartesian-acquired images tended towards improved denoising, artifact reduction and tracking performance compared to the radially-acquired images. One reasoning for this is that the radial data were acquired with a golden-angle increment, leading to a varying appearance of undersampling artifacts between frames in the image time series. In this case the U-net data training may have had difficulty in learning these artifacts, in comparison to the static appearance of the Cartesian undersampling artifacts.

In terms of tumor tracking, it should be acknowledged that the U-net based tracking method was surprisingly effective at tumor tracking in images without denoising, in which very few features were visible in the images. However, denoising improved the stability of the tumor tracking in the case of high undersampling factors. A larger patient cohort containing different tumor shapes and contrasts, and a variety of breathing patterns would be required to extract the potential trends in these data.

The use of parallel imaging in the denoising process was found to have only a small impact on tumor tracking. As a single frame of denoised data can be processed within 53 ms, after learning, on standard desktop hardware, this allows for an online implementation of this technique.

Conclusion

Image denoising using U-net allows for a fast, potentially online, method for reducing noise and the appearance of undersampling artifacts in highly undersampled cine images used in tumor tracking in MR-guided radiotherapy.

Acknowledgements

No acknowledgement found.