4202
Acoustic and sampling optimization of 3D Radial MRI using neural network optimization1Department of Medical Physics, University of Wisconsin-Madison, Madison, WI, United States, 2Department of Radiology, University of Wisconsin-Madison, Madison, WI, United States, 3University of Wisconsin-Madison, Madison, WI, United States
Synopsis
3D radial sampling can enable ultrashort echo times, reduce sensitivity to motion, and provide high levels of acceleration. These methods have recently been used to perform free-running pediatric body imaging. However, the optimization of projection sampling remains an open problem and current schemes often produce high acoustic noise with an unfavorable noise texture. In this work, we demonstrate the optimization of trajectories using a joint consideration of sampling and acoustic performance. To perform this we introduce a neural network framework and investigate variable TR optimization as means to simultaneously distribute projections optimally and minimize acoustic noise autocorrelation.
Introduction
3D-radial MRI has been proposed to provide motion resolved, ultrashort echo time, and highly accelerated imaging. To achieve this, methods have been proposed to design projection angles and their sampling order using reordering of spiral on a spherical surface1, spherically mapped 2D golden means 2, and phyllotaxis sampling3, among others. These techniques aim to minimize artifacts caused by clustering of projections, which often arises when sub selecting data in time, and/or respiratory/cardiac position.. These techniques hold two challenges: (1) the design choices are often heuristic and may not produce the ideal sampling, especially when irregular gating is applied, and (2) the acoustic noise generated by these sequences is often high and of an unfavorable texture. The acoustic aspect is especially detrimental for pediatric and functional imaging, where it may in turn translate to bulk motion, alter physiology, and increase patient anxiety. Previous efforts have been made towards hardware design3 and bandlimited gradients5,6. In this work, we propose a neural network based framework to allocate the spatial and temporal location of the projections and also a variable TR shift optimization to achieve more uniform sampling and preferable acoustic noise features.Methods
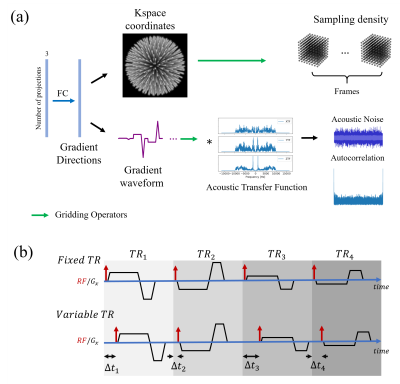
Our approach is based on a procedure as illustrated in Figure 1 (a), consisting of a neural network based trajectory generator, acoustic noise simulation, and losses based on sampling density and acoustic autocorrelation. All components in the chain are differentiable, allowing for back-propagation and gradient based optimization in a GPU accelerated framework based on a combination of PyTorch7 and SigPy8. Trajectory generation uses fully connected layers to learn directions that would scale the base gradient waveforms. From this, k-space coordinates are generated and also a gradient which is used for acoustic simulation. In one realization of this architecture, we also allow for variable TRs, as shown in Figure 1(b), where the position of the gradients and RF, a learned parameter, is allowed to vary. The delay is such that the average TR is the desired TR and no delay is greater than the dead time in a TR without delay. (autocorrelation). Acoustic sound pressure waves were simulated by convolving the gradient waveforms with acoustic transfer functions provided by the vendor. Noise waveforms are used to calculate the autocorrelation which is minimized. Gridding of k-space coordinates to a 4D (3D+time) array enables optimization spatiotemporal uniformity using the L2 norm of the sampling density estimate, with the net loss being a weighted sum of sampling and acoustic autocorrelation loss.Experiments Two sets of projections were generated by the neural network, one being 10,000 projections without 4D sampling uniformity for static reconstruction and the other being 15,000 projections with 4D sampling uniformity for dynamic reconstruction. Ultrashort echo time (UTE) scans of phantom and volunteers were performed on 3.0T with 10,000 projections, TR=2.4 ms, flip angle=4 $$$^{\circ}$$$. Exemplary human scans were acquired with TR=0.1/2.4 ms for scans without gradient shift and TR=5.1 ms for scans with gradient shift.
Results
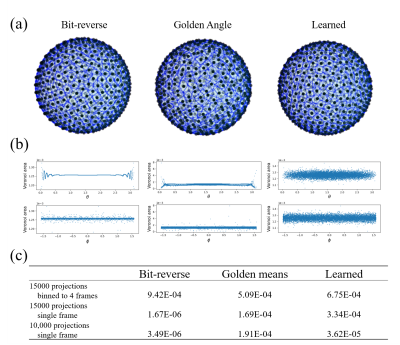
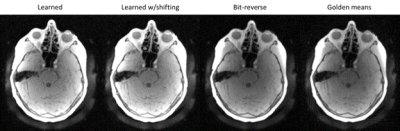
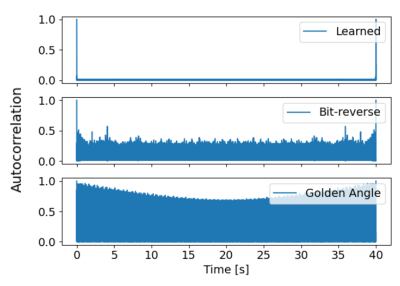
Figure 2 shows spherical Voronoi areas for bit-reverse, golden angle and learned approach (500 projections for the purpose of illustration) and the Voronoi areas dependencies on polar and azimuthal angle. Both bit-reverse and golden angle approach show significant dependency on $$$\theta$$$ while the learned method shows none. Also shown in figure 2 (c) is the standard deviation of Voronoi areas. The learned distribution showed comparable results to the two existing methods. However, as the 15,000 projections were optimized with gridding to 40 frames in time, and it shows higher standard deviation for all projections compared with the other two methods, which indicates that the gating performance of the network has room for improvement.Figure 3 shows results from phantom scan. Both golden angle and bit-reverse shows asymmetric coherent artifacts due to the dependency of sampling density on $$$\theta$$$. Whereas the images acquired with neural network based projections scan shows overall better image quality. Results from a volunteer scan are shown in figure 4. Golden means sampling shows more significant streaking artifacts than others. As for the aspect of minimizing acoustic noise autocorrelation, figure 5 illustrates that the learned approach yields not correlated noise compared with golden angle and bit-reverse.
Discussion and conclusion
We demonstrated that a more uniform distribution of radial projections and a whiter acoustic noise could be learned via unsupervised learning. We showed that the image quality of learned trajectories could be better than both existing methods. However the optimization of the learned methods is heuristic currently, with fixed width Hann kernels for kspace and linear kernel for gradient waveform. Potentially, iterative weights estimation could be incorporated into the framework allowing the kernel to be optimized. Moreover, what would be a good metric for acoustic noise remains an open and subjective question. Also, more accurate transfer functions could be measured. Future work could be done in exploring these aspects to improve this framework.Acknowledgements
We gratefully acknowledge research support from GE Healthcare and funding from NIH R01 HL136965.References
1. H. K. Song, L. Dougherty, and M. D. Schnall, “Simultaneous acquisition of multiple resolution images for dynamic contrast enhanced imaging of the breast,” Magn. Reson. Med., vol. 46, no. 3, pp. 503–509, Sep. 2001, doi: 10.1002/mrm.1220.
2. R. W. Chan, E. A. Ramsay, C. H. Cunningham, and D. B. Plewes, “Temporal stability of adaptive 3D radial MRI using multidimensional golden means,” Magn. Reson. Med., vol. 61, no. 2, pp. 354–363, 2009, doi: 10.1002/mrm.21837.
3. D. Piccini, A. Littmann, S. Nielles‐Vallespin, and M. O. Zenge, “Spiral phyllotaxis: The natural way to construct a 3D radial trajectory in MRI,” Magn. Reson. Med., vol. 66, no. 4, pp. 1049–1056, 2011, doi: https://doi.org/10.1002/mrm.22898.
4. A. Katsunuma, H. Takamori, Y. Sakakura, Y. Hamamura, Y. Ogo, and R. Katayama, “Quiet MRI with novel acoustic noise reduction,” Magn. Reson. Mater. Phys. Biol. Med., vol. 13, no. 3, pp. 139–144, Oct. 2001, doi: 10.1007/BF02678588.
5. F. Hennel, F. Girard, and T. Loenneker, “‘Silent’ MRI with soft gradient pulses,” Magn. Reson. Med., vol. 42, no. 1, pp. 6–10, 1999, doi: https://doi.org/10.1002/(SICI)1522-2594(199907)42:1<6::AID-MRM2>3.0.CO;2-D.
6. J. Hutter et al., “Quiet echo planar imaging for functional and diffusion MRI,” Magn. Reson. Med., vol. 79, no. 3, pp. 1447–1459, 2018, doi: 10.1002/mrm.26810.
7.A. Paszke et al., “PyTorch: An Imperative Style, High-Performance Deep Learning Library,” Adv. Neural Inf. Process. Syst., vol. 32, pp. 8026–8037, 2019.
8. “(ISMRM 2019) SigPy: A Python Package for High Performance Iterative Reconstruction.” http://archive.ismrm.org/2019/4819.html (accessed Dec. 16, 2020).
Figures