Introduction

Parallel imaging (PI) is a central technique in MRI applications for achieving shorter scan times. Despite the abundance of advanced methods and algorithms, a large proportion of PI applications employ regular Cartesian undersampling and reconstruction. However, more general non-Cartesian sampling trajectories promise improved PI performance. Recently, the MRzero framework¹ has been proposed for automated MR sequence generation based on differentiable Bloch simulations and a supervised learning approach. In the present work, MRzero is extended by PI capability and first steps towards full sequence optimization including non-Cartesian k-space trajectories for improved PI performance are presented.

Methods

MRzero is a fully differentiable Bloch-equation-based MR simulation that mirrors the acquisition on a real MR scanner. By that, it allows for an analytic derivative-driven non-linear optimization of sequence parameters like spatial encoding gradients (2D), RF pulses and timing of sequence events. Details on the MRzero implementation are given in¹. In the original single-channel approach, image reconstruction was performed via the adjoint of the encoding operator composed of the known k-space locations . To enable parallel imaging with arbitrary k-space trajectories, we employ CG SENSE² by forming the multi-channel image encoding operator
$$\boldsymbol{E}_{(r,m),n} = B_{1,r}^-(\boldsymbol{x}_n) \exp(\text{i} \boldsymbol{k}_m \cdot \boldsymbol{x}_n)$$
with coil sensitivities $$$B_{1,r}^-$$$ of the r-th channel at voxel locations $$$\boldsymbol{x}_n$$$. A reconstructed image $$$\boldsymbol{m}_\text{reco}$$$ can then be formed from the multi-coil k-space signal $$$\boldsymbol{s}_r$$$ by solving the linear equation system $$$\boldsymbol{E}^H\boldsymbol{E} \boldsymbol{m}_\text{reco}=\boldsymbol{E}^H \boldsymbol{s}_r$$$ with the CG algorithm. Expressing CG reconstruction as a function $$$\boldsymbol{m}_\text{reco}=f(\boldsymbol{s}_r)$$$ allows formulating the optimization objective function for the sequence parameters $$$\Psi$$$ as
$$\Psi^*=\underset{\Psi}{\text{arg min}} ||\boldsymbol{m}_\text{target} - f(\text{SCANNER}(\Psi,\Phi)\boldsymbol{m}_0)||_2^2 + R(\Psi)$$
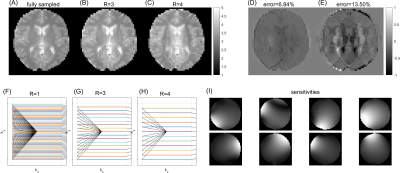
with the forward simulation operator $$$\text{SCANNER}(\Psi,\Phi)$$$ as described in ¹ and the desired target image $$$\boldsymbol{m}_\text{target}$$$. In this work, the regularization $$$R(\Psi)$$$ included additional terms penalizing both high g-factors and the trajectory exceeding k-space boundaries. Despite the iterative reconstruction represented by $$$f$$$, the loss function is still differentiable with respect to the sequence parameters $$$\Psi$$$, which allows for efficient gradient descent optimization as in the original MRzero approach. As target for the optimizations, simulated reconstruction of a fully sampled Cartesian FLASH sequence (matrix size 48x48, flip angle FA=5°, TR=8 ms) on a numerical brain phantom was used. Realistic coil sensitivities for simulations were obtained from a 20ch Rx head coil by performing a fully sampled phantom scan (Figure 1I).

Results

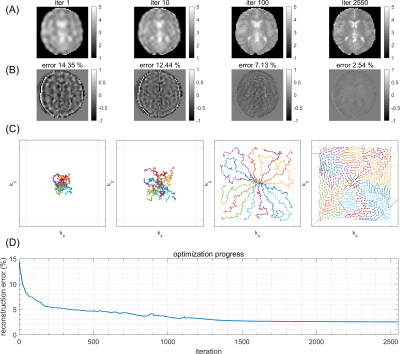
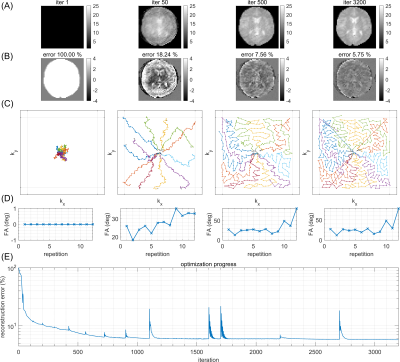
Figure 1A shows the target image simulated from a fully sampled Cartesian FLASH sequence (Figure 1A). Cartesian undersampling of this trajectory (Figure 1B,C) leads to reconstruction artifacts, which can be observed in the difference maps (Figure 1D,E). Learned free non-Cartesian trajectories can improve the reconstruction of undersampled datasets: Figure 2 shows iterations of such an optimization for acceleration R=3, starting with an initialization at random sampling locations close to k-space center, which spread over iterations to finally cover the entire k-space (Figure 2C). This yields increasingly better reconstructions (Figure 2A) with lower prediction error (Figure 2B), converging to a solution with reconstruction error clearly below the regularly undersampled Cartesian case (Figure 1B,D). Next, the potential of MRzero for full sequence parameter optimization was addressed. For this, additionally, the FA of each RF excitation pulse were initialized at zero and left as free optimization parameters. To make the optimization task more difficult, for the target FLASH sequence, FA was increased to 25° and TR to 20 ms, whereas for the optimization, TR was fixed at 8 ms. This enforces learning a variable FA pattern to compensate for blurring induced by transient signal decay. Figure 3A,B shows that for acceleration R=4 this learned sequence yields reconstruction errors below 6%, again clearly below the Cartesian undersampling case (Figure 1C,E). The learned variable FAs (Figure 3D) show a plausible pattern of increasing FA over repetitions.

Discussion

The conducted simulation experiments showed that deviating from regular Cartesian undersampling can provide better PI reconstructions. This is not surprising, as incoherent undersampling spreads the aliasing artifact across the entire image, which makes this a key ingredient of compressed sensing techniques⁴. Thus, extending the MRzero reconstruction by such techniques or even deep learning reconstructions would thus be a next logical step. Recently, there have been several works on learning-based non-Cartesian trajectory optimization for both single-channel^5,6 and PI acquisition^7,8. Although MRzero cannot yet compete with these approaches in terms of achievable resolution, it has the advantage of a very general formulation of the MR acquisition. This enables not only optimization of sampling trajectories, but also joint optimization of all sequence parameters, like RF pulses and timings, and the reconstruction process according to a target contrast of interest. For realistic application, as a next step, hardware limitations of the gradient system, i.e. maximum gradient strengths and slew rates, need to be taken into account, which can e.g. be formulated as additional penalty terms in the loss function.

Conclusion

Parallel imaging was incorporated into the MRzero framework, enabling full supervised optimization of sequence parameters, including non-Cartesian k-space trajectories for multi-channel acquisitions and variable excitation flip angles. This offers the potential of finding acquisition schemes that are better suited for parallel imaging than conventional Cartesian undersampling. As this was shown herein for simulated data only, next steps will focus on translating the results to a real MR system.

Acknowledgements

Financial support of the Max-Planck Society and ERC Advanced Grant "SpreadMRI", No 834940 is gratefully acknowledged.