Introduction

Many advanced pulse sequences combine contrast-preparation modules, like T1, T2, diffusion or perfusion weighting, with an efficient acquisition scheme for high resolution, large spatial coverage, or both. This requires a low-high profile order to ensure the k-space center be acquired at the beginning of the readout to preserve the prepared contrast. A long readout to fill the rest of the k-space would be desired for speedy acquisition. Typical fast imaging methods include turbo-filed-echo (TFE), ¹ balance steady-state-free-precession (bSSFP) ² and turbo-spin-echo (TSE). ³ k-Space data are filtered by a modulation transfer function (MTF) due to magnetization relaxation during the acquisition, which may cause signal/contrast loss and blurring, ^4,5 and is studied limitedly using the image-space point spread functions (PSF). ^5,6 For TSE with 180° refocusing, T2 relaxation is the main effect for PSF; ⁵ For TFE and bSSFP, analytical characterization of relaxation-induced PSF has not been studied, as multiple factors (T1/T2, flip angle and TR) interact together. Here, we derived the analytical formulations of the MTF and PSF for Cartesian TFE, bSSFP for the first time, which are compared to TSE. The contrast-to-noise ratio (CNR) is defined and maximized with optimal TFE/TSE factor (N), flip angles (FA, α).

Theory

TFE
The transient-state transverse signal after the $$$n^{th}$$$ excitation pulse is: $$M_{xy}(n)=A\varepsilon^{n-1}+B,$$$$A=M_z(0)E_2\sin\alpha-B,\quad B=\frac{M^0(1-E_1)}{1-\varepsilon}E_2\sin\alpha.$$ Here, $$$\varepsilon=e^{-TR/T1}\cos\alpha$$$, $$$M_z(0)$$$ is the initial longitudinal signal, $$$E_1=e^{-TR/T1}$$$, $$$ E_2=e^{-TE/T2^*}$$$ and $$$M^0$$$ is the equilibrium signal.
MTF at k-space location $$$k\in[-0.5, 0.5]$$$ with a low-high profile order in a single phase encoding direction is: $$MTF(k)=M_{xy}(2|k|N)=A\varepsilon^{2|k|N}+B.$$The corresponding PSF in the image domain is: $$PSF(x)=A\frac{\varepsilon^N(N\ln\varepsilon\cos(\pi x)+\pi x\sin(\pi x))-N\ln\varepsilon}{N^2\ln^2\varepsilon+\pi^2x^2}+B\ \text{sinc}(\pi x).$$The peak amplitude is a linear function of $$$M_z(0)$$$: $$PSF(0)=\frac{A(\varepsilon^N-1)}{N\ln\varepsilon}+B=\text{Slope}\ M_z(0)+\text{Intercept},$$ $$\text{Slope}=\frac{\varepsilon^N-1}{N\ln\varepsilon}E_2\sin\alpha,\quad\text{Intercept}=(1-\frac{\varepsilon^N-1}{N\ln\varepsilon})B.$$Based on this linearity, we define the CNR as the slope multiplied by an offset of SNR gain from an extended acquisition window ($$$ACQ=NTR$$$), which is proportional to $$$\sqrt{ACQ}$$$: $$CNR_{TFE}=\text{Slope}\sqrt{NTR}=\frac{\varepsilon^N-1}{\ln\varepsilon}\sqrt{\frac{TR}N}E_2\sin\alpha.$$Theoretically, $$$CNR_{TFE}$$$ is monotonically increasing with TR. For a fixed TR, there is an optimal solution: $$N^*=\frac{1.26}{\tau-0.5\ln{q(\tau)}},\quad \alpha^*=\arccos\sqrt{q(\tau)},\quad CNR_{TFE}^*=0.64\sqrt\frac{TR(1-q(\tau))}{\tau-0.5\ln{q(\tau)}}E_2.$$Here $$$\tau=\frac{TR}{T1}$$$, and $$$q(\tau)\in(0, 1)$$$ is a solution of the transcendental equation $$$-q\ln q+(1+2\tau)q-1=0$$$.

bSSFP
For bSSFP, the MTF assuming TE=TR/2 is: $$MTF(k)=A\lambda^{2|k|N}+B.$$$$A=M_z(0)\sin\frac{\alpha}2-B,\quad B=\frac{M^0\sqrt{E_2}(1-E_1)\sin\alpha}{1-(E_1-E_2)\cos\alpha-E_1E_2}.$$Here $$$\lambda=E_2\sin^2(\frac{\alpha}2)+E_1\cos^2(\frac{\alpha}2)$$$, and note that $$$E_2=e^{TR/T2}$$$ in bSSFP. ⁷
The corresponding PSF is: $$PSF(x)=A\frac{\lambda^N(N\ln\lambda\cos(\pi x)+\pi x\sin(\pi x))-N\ln\lambda}{N^2\ln^2\lambda+\pi^2x^2}+B\ \text{sinc}(\pi x).$$The peak amplitude is also a linear function of $$$M_z(0)$$$: $$PSF(0)=\frac{A(\lambda^N-1)}{N\ln\lambda}+B=\text{Slope}\ M_z(0)+\text{Intercept},$$ $$\text{Slope}=\frac{\lambda^N-1}{N\ln\lambda}\sin\frac{\alpha}2,\quad\text{Intercept}=(1-\frac{\lambda^N-1}{N\ln\lambda})B.$$The CNR of bSSFP is monotonically increasing with TR and there is an optimal solution for each TR:$$CNR_{bSSFP}=\frac{\lambda^N-1}{\ln\lambda}\sqrt{\frac{TR}N}\sin\frac{\alpha}2.$$$$N^*=\frac{1.26}{\ln m},\quad \alpha^*=\arccos\frac{2m-E_1-E_2}{E_1-E_2},\quad CNR_{bSSFP}^*=0.64\sqrt\frac{TR(E1-m)}{-(E_1-E_2)\ln m}.$$Here $$$m=max\{q(E_1),E_2\}$$$, and $$$q(E_1)$$$ is a solution of the transcendental equation $$$-q\ln q+q-E_1=0$$$.
When $$$T1<\frac{-TR}{-TR/T2+\ln{(1+TR/T2)}}$$$, $$$\alpha^*=180^{\circ}$$$. In this case, a smaller FA can be chosen with some CNR sacrifice characterized by the factor $$$\eta$$$: $$N_{\eta}^*=\frac{1.26\eta^2T2}{xTR},\quad \alpha_{\eta}^*=2\arccos\sqrt x,\quad CNR_{\eta,bSSFP}^*=\eta CNR_{bSSFP}^*.$$Here $$$x$$$ is the solution of the transcendental equation $$$\frac{x\ln E_2}{\ln{(E_2x+E_1-E_1x)}}=\eta^2$$$.

TSE
This work focuses on TSE with only 180° refocusing pulses. The MTF is: ⁵$$MTF(k)=M_z(0)E_2e^{2|k|r}.$$Here $$$ E_2=e^{-ESP/T2}$$$ and $$$ r=\frac{ESP\times N}{T2}$$$, where ESP is the echo spacing.
The PSF is: ⁵$$PSF(x)=M_z(0)E_2\frac{e^{-r}(\pi x\sin(\pi x)-r\cos(\pi x))+r}{r^2+\pi^2x^2}.$$The peak amplitude is proportional to $$$M_z(0)$$$: $$PSF(0)=\frac{1-e^{-r}}rE_2M_z(0).$$The CNR is: $$CNR_{TSE}=(1-e^{-r})E_2\sqrt\frac{T2}r.$$It is maximized ($$$=0.64E_2\sqrt{T2}$$$) when $$$r=1.26$$$. ⁵ The optimal CNR will decay monotonically with longer ESP.

Methods

Transcendental equations are solved numerically in MATLAB (Mathworks Inc.). An example is studied with T1=1000ms, T2=100ms and T2*=50ms. We chose some typical sequences in this example: TFE (TR/TE=10/1.5ms), bSSFP (TR/TE=5/2.5ms) and TSE (ESP=10ms). The optimal choice of some other typical pairs of T1 (250-4000ms) and T2 (40-2000ms) values are also given.

Results

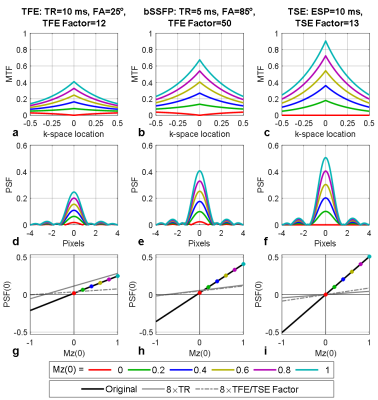
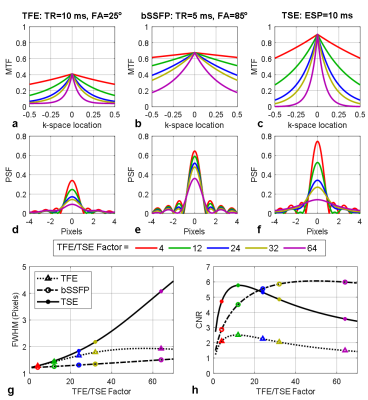
Figures 1 demonstrates the MTF (top) and PSF (middle) of variant M_z(0), and the linearity of peak-amplitude and Mz(0) (bottom) of typical TFE, bSSFP and TSE sequences. TFE has the largest peak-amplitude loss and large intercept (bias) increase when TR is 8× prolonged. The peak-amplitude loss of TSE is minimum.

Figure 2 demonstrates the MTF (top) and PSF (middle) of different TFE/TSE factors, and corresponding FWHM and CNR (bottom). FWHM of TFE (1.2-2pixels) and bSSFP (1.2-1.6pixels) are increased slower than TSE (1.2-4.5pixels). CNR* of bSSFP and TSE are similar (~6). Compared to TSE (N*=~13), bSSFP achieves this optimal CNR with a much larger TFE factor (N*=~50).

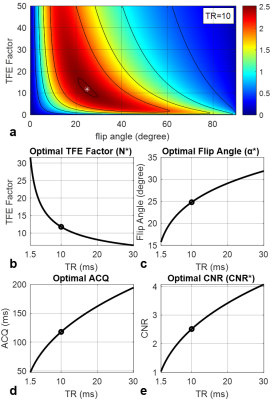
Figure 3a shows a concave CNR map of the TFE sequence at TR=10ms as a function of FA and TFE factor. The maximum CNR (2.51) found at N*/α*=12/25° meets the analytical solution. Figures 3b-3e shows monotonically decreasing N* and increasing α*, ACQ, and CNR*_TFE as TR increases.

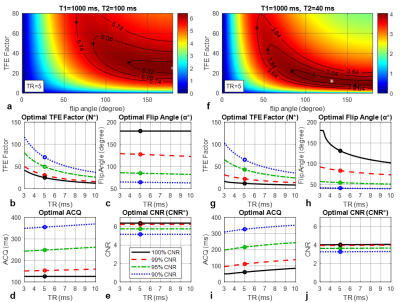
Figures 4a-4e and Figures 4f-4j demonstrate CNR maps and N*,α*, ACQ and CNR*_bSSFP with two different T1/T2 values. When T1=1000ms and T2=100ms, $$$T1<\frac{-TR}{-TR/T2+\ln{(1+TR/T2)}}$$$ and the optimal 100%, 99%, 95% and 90% CNR with α*/N*=180°/25, 128°/31, 85°/50 and 64°/71, meet the analytical solution. For all 3ms≤TR≤10ms, small CNR sacrifice (1%-10%) lead to a large decrease in FA (52°-116°) and increases in TFE Factor and ACQ.

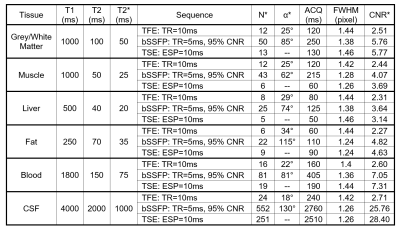
Table 1 provides the analytical solutions of N*, α*, ACQ, FWHM and CNR* of the selected TFE, bSSFP and TSE sequences with some typical T1/T2/ T2* values.

Discussion and Conclusion

This work provides guidance to choose TFE, bSSFP and TSE parameters based on analytical formulation, which is also a useful tool to analyze and compare signal loss and blurring effects. Considering CNR and FWHM, bSSFP is especially suitable for large TFE factors. Long TR and short TE are suggested for TFE, suitable for spiral acquisitions.

Acknowledgements

No acknowledgement found.