4197
Achieving High Spatial Resolution with Dual Polarity Missing Pulse Steady-State Free Precession in a Clinically Relevant Scan Time1Center for Magnetic Resonance Research and Department of Radiology, University of Minnesota, Minneapolis, MN, United States
Synopsis
Clinical MRI sequences for imaging near metallic implants are mainly multi-spectral approaches, with fast spin-echo acquisitions and large acceleration factors to achieve clinically relevant scan times. The authors previously reported a broadband, low flip angle method at 1.5T to image with large field inhomogeneity, such as near metallic implants, quickly relative to non-spatially selective multispectral approaches. Herein it is demonstrated that this approach, dual polarity missing pulse steady-state free precession, can achieve high spatial resolutions at 3T with a large 3D FOV in a clinically relevant scan time, ~8.74 minutes.
Purpose
A small number of sequences are currently available for MR imaging near metallic implants in a clinically relevant scan time (1-3) due to the large induced field inhomogeneities. While the accuracy and efficiency of dual polarity missing pulse steady-state free precession (MP-SSFP) has previously been demonstrated at 1.5T, the spatial resolution was 2mm isotropic, the scan time was 14 minutes, and the signal-to-noise ratio (SNR) was approximately 12 (4). Here, a high spatial resolution of 1mm isotropic is achieved with a large, 256mm3 FOV. The MP-SSFP sequence parameters have been tuned and experiments were performed at 3T to boost SNR. Parallel imaging was employed to attain clinically relevant scan times, using each gradient polarity acquisition as a set of virtual coils to improve the reconstruction.Methods
The Missing Pulse Steady-State Free Precession (MP-SSFP) (5) sequence was used, whereby a train of n small-flip angle pulses are applied to achieve a steady-state. Data are acquired in place of the n+1 pulse, where an echo forms. This sequence achieves radiofrequency (RF) refocusing with low peak amplitude. The dual polarity encoding was implemented such that acquisition of the same phase encoding line for each gradient polarity was separated by a single TR to limit motion artifacts. The displacement field was estimated by aligning the intensity-corrected, resampled magnitude images resulting from the opposing gradient polarities, parameterizing the displacement in terms of 3D B-splines (6).Phantom experiments were performed on a 3T Siemens Prisma scanner using a 32-channel head coil. The phantom consisted of agar with one stainless steel and one titanium screw embedded inside. Acquisitions were fully sampled experimentally and retroactively undersampled in the phase encoding dimensions (R=3x2) for this demonstration. The MP-SSFP sequence used n=4 pulses, TR=24ms, and 650 Hz/pixel receiver bandwidth. Hyperbolic secant (7) pulses were used, with time-bandwidth product 10, 500µs duration, 20kHz bandwidth, and 20˚ flip angle. The field-of-view (FOV) was 256x256x256 mm3 with 1mm isotropic resolution, and total scan time of 52.43 minutes. The retroactively undersampled acquisition would have taken 8.74 minutes.
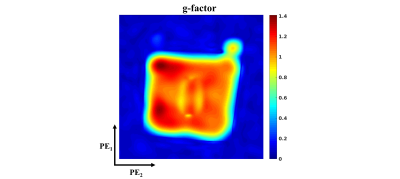
GRAPPA (8) was used for parallel imaging, with a 24x24 autocalibrating signal (ACS) region in the phase encoded dimensions. The ACS data were not included in the final reconstruction. The 2D GRAPPA reconstructions were performed per plane in the frequency encoding direction following Fourier Transform in that dimension of the data. The reconstruction was performed with data from each polarity concatenated along the coil dimension to increase the number of effective coils, similar to the virtual coil technique introduced by Blaimer et al. (9). A noise-only scan was used to correct for noise correlations between coils. The g-factor was determined using the analytical method introduced by Breuer et al. (10). The GRAPPA-reconstructed images were used as inputs for the distortion correction algorithm, which used 3mm spline knot spacing to estimate the displacement field.
Results
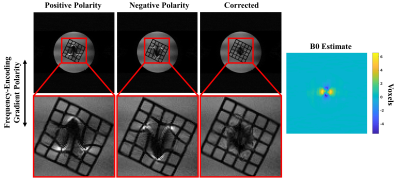
A comparison between the fully sampled and GRAPPA-reconstructed images is shown in Fig. 1 as one cross section along the frequency encoded dimension. The residual aliasing artifacts are not significant, as seen in the difference image of Fig. 1. Noise amplification is pronounced, (g-factor in Fig. 2), but the SNR remains acceptable in the reconstructed image, with a peak value of ~36 in the cross section shown in Fig. 1, as determined using an SNR unit reconstruction (11).The distortion corrected image is shown in Fig. 3 with a B0 estimate in voxel units. The geometric and intensity distortions are clearly corrected, but there is too little spatial encoding closer to the metal to accurately reconstruct the image, due to large intrinsic field gradients.
Discussion
The primary disadvantage of the MP-SSFP technique described here is the absence of slab selection, which would permit a shorter scan time. While slab selection is possible, phase encoding remains necessary in the spatially-selected dimension (1,3) to resolve slab distortions. On the contrary, the short TR of MP-SSFP alleviates the need for spatial selection.A common problem with Partial Fourier (PF) occurs in regions with rapid image phase variation, due to the inability to correct such phase variation with the symmetrically sampled portion of k-space. In contrast to MSI sequences, PF acceleration is suboptimal with dual polarity MP-SSFP, which simultaneously excites a broad bandwidth, leading to rapid phase variations near metallic implants. MSI sequences avoid this issue by only imaging a narrow bandwidth at any time. Hence, a small PF factor is acceptable but is not useful for substantial acquisition time reduction when using MP-SSFP as performed herein.
Compared to 1.5T, imaging near metallic implants at 3T requires higher bandwidth pulses to excite spins in close proximity to the metal. Even if excited, a large frequency encoding gradient is required to overcome the intrinsic field inhomogeneity sufficiently for the distortion correction technique presented here to successfully recover the undistorted image.
Future work will examine 2D CAIPIRINHA (12) in conjunction with dual polarity MP-SSFP to decrease noise amplification in GRAPPA. A unique feature which will permit a wider range of possible undersampling schemes is the sequential acquisition of each polarity image, so that the k-space sampling patterns for each set of virtual coils need not be the same.
Acknowledgements
This work was supported by the National Institutes of Health grants U01 EB025153 and P41 EB025144-01.References
1. Koch KM, Brau AC, Chen W, Gold GE, Hargreaves BA, Koff M, McKinnon GC, Potter HG, King KF. Imaging near metal with a MAVRIC-SEMAC hybrid. Magn Reson Med 2011;65(1):71-82.
2. Koch KM, Lorbiecki JE, Hinks RS, King KF. A multispectral three-dimensional acquisition technique for imaging near metal implants. Magn Reson Med 2009;61(2):381-390.
3. Lu W, Pauly KB, Gold GE, Pauly JM, Hargreaves BA. SEMAC: Slice Encoding for Metal Artifact Correction in MRI. Magn Reson Med 2009;62(1):66-76.
4. Mullen M, Garwood M. Reverse-Encoding MRI Near Metallic Implants Using Missing Pulse Steady-State Free Precession. In: ISMRM & SMRT Virtual Conference and Exhibition, 2020. p 3404.
5. Patz S, Wong ST, Roos MS. Missing pulse steady-state free precession. Magn Reson Med 1989;10(2):194-209.
6. Skare S, Andersson JL. Correction of MR image distortions induced by metallic objects using a 3D cubic B-spline basis set: application to stereotactic surgical planning. Magn Reson Med 2005;54(1):169-181.
7. Silver MS, Joseph RI, Hoult DI. Highly selective π/2 and π pulse generation. Journal of Magnetic Resonance (1969) 1984;59(2):347-351.
8. Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med 2002;47(6):1202-1210.
9. Blaimer M, Gutberlet M, Kellman P, Breuer FA, Kostler H, Griswold MA. Virtual coil concept for improved parallel MRI employing conjugate symmetric signals. Magn Reson Med 2009;61(1):93-102.
10. Breuer FA, Kannengiesser SA, Blaimer M, Seiberlich N, Jakob PM, Griswold MA. General formulation for quantitative G-factor calculation in GRAPPA reconstructions. Magn Reson Med 2009;62(3):739-746.
11. Kellman P, McVeigh ER. Image reconstruction in SNR units: a general method for SNR measurement. Magn Reson Med 2005;54(6):1439-1447.
12. Breuer FA, Blaimer M, Mueller MF, Seiberlich N, Heidemann RM, Griswold MA, Jakob PM. Controlled aliasing in volumetric parallel imaging (2D CAIPIRINHA). Magn Reson Med 2006;55(3):549-556.
Figures