Introduction

A MP-RAGE sequence is composed of the repetition of segments divided in three steps: (1) a magnetization preparation for contrast control, (2) data acquisition with a short time of repetition (TR) and low flip angle spoiled gradient echo scheme, and (3) a partial recovery step. Short segments and their rapid succession lead to a longitudinal steady state (contribution of transverse magnetization is destroyed).This Flash-type acquisition allows flexible contrasts. MP-RAGE is generally used in combination with an inversion preparation to generate T1 contrast. Nevertheless, it can be anticipated that contrast could be improved by playing both on T1 and T2 relaxations. This requires the optimization of more complex preparation schemes, which cannot be solved straightforwardly. Thus, an optimal control (OC) framework that allows longitudinal steady state is developed, based on the GRAPE algorithm^{2, 3}. The interest of our optimized preparation is quantified and demonstrated in vitro and in vivo on rat brain, for different segment duration.

Methods

Unlike previously proposed OC preparation schemes that considered full magnetization recovery^{4, 5}, the proposed framework takes into account the formation of a longitudinal steady state. More precisely, the action of the preparation on the magnetization is modelled by successive matrix multiplications and any transverse magnetization is assumed to be adequately spoiled before the preparation and potentially after. Then the condition of equilibrium gives a general expression of the longitudinal steady state as a function of acquisition parameters and preparation parameters that become variables of the considered optimization problem.The cost function used in the OC problem aims at maximizing the contrast when acquiring the central line of the k-space:

$$C =\alpha S_{a,i}^2 -S_{b,i}^2$$

$$$\alpha$$$ : weighting coefficient (10 in our case).
$$$S_{a/b,i}$$$ : signal intensity of tissue a, to be saturated, or tissue b, to be maximized, after the ith flip angle excitation of the gradient echo acquisition in a cycle, once the macro steady state is achieved.

The adequacy between theoretical and experimental contrast results were checked in vitro on tubes (glycerol + NiSO4). Relaxation times were measured and the optimized sequences were computed and applied on a 11.7T Bruker system to saturate the signal of one sample a (T1/T2 (ms): 719/76) and maximize the signal of one sample b of shorter T1 and T2 (T1/T2 (ms): 454/25) for different segment durations (from 4s to 0,5s). The matrix size was 128x128x16 pixels, segments of 32 readout were performed with centric encoding, an echo repetition time of 6.5ms and a 13° flip angle.

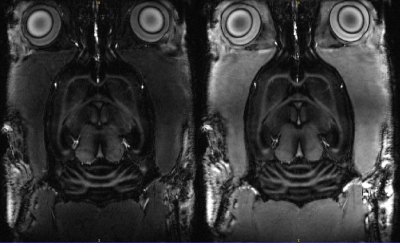
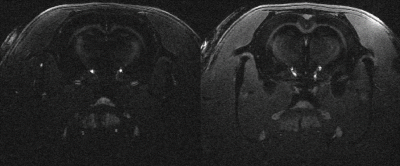
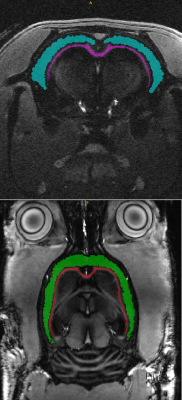
The sequences to enhance contrast between cortex (T2/T1 (ms): 34,2/1945) and corpus callosum (T2/T1 (ms): 31,2/1710 ) in the rat brain were optimized with the proposed OC framework and applied on Brucker 11.7T MRI preclinical scanner, for different segment duration from 3s to 1s. Two rat brains were scans: in coronal (first rat) and axial and coronal slices (second rat). Compared to previous in vitro acquisition, in-plane matrix was resized to 256x256 but other parameters were kept unchanged.

In each case, a preparation scheme of one pulse and two pulses were optimized (refocusing pulses are not counted).

Results

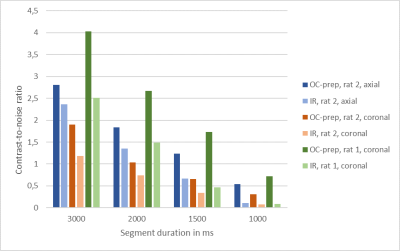
The proposed optimization method founds an inversion-recovery (IR) for one pulse preparation, and a T2prep-IR for two pulses preparation (referenced as OC-prep) for both in vitro like in vivo experiments. In vitro, we found a good correlation between the experimental contrast and the numerically predicted contrast for IR and OC-prep for different segment duration, with a contrast match ranging from 73% to 97%. In vivo an increase of the contrast-to-noise ratio between cortex and corpus callosum was obtained with OC-prep compared to IR prep over the two rats, for the four different segment duration and the different slices orientations (figure 2). This increase is at least 18% and exceeds 500% for segment duration of 1s, but in this case with a simple IR the signal is so slow that it is melted into the noise. The gain in contrast-to-noise ratio of OC-prep compared with IR is larger as segment duration decreases. In vivo, the increase lies between 83% and 274% for a segment duration of 1,5s, against only between 18% and 61% for a segment duration of 3s.

Discussion

In this present case, when seeking to maximize signal of short T1 and T2 tissues, the optimization results in a T2prep-IR scheme, which is a known solution that plays on T2 differences to enhance T1 contrast. The advantage here is that optimal pulse parameters (timing and flip angles) are computed automatically. Moreover, the proposed framework is generic and allows to optimize a preparation of an arbitrary number of pulses that could be used for more difficult contrast objectives such as involving three different tissues. Both in vitro and in vivo experiments suggest that the benefit of the CO-prep with respect to IR increases as the TR decreases. The proposed scheme is thus able to generate a better contrast-to-noise ratio in shorter acquisition times due to faster T2 relaxation.

Conclusion

Magnetization preparations optimized by the GRAPE algorithm that use both T1 and T2 relaxations allows to enhance contrast between brain tissues and most importantly for short acquisition times. Other developments are under study to integrate more acquisition parameters (TR, FA) into the optimization.

Acknowledgements

This work was performed on the platform PILoT, and by a laboratory member of France Life Imaging network (grant ANR-11-INBS-0006) and within the framework of LABEX PRIMES ANR-11-LABX-0063/ ANR-11-IDEX-0007.