4169
T2-Shuff-LL: Multi-contrast 3D Shuffling Combining Fast Spin-Echo and Look-Locker Gradient Echo
Jonathan Tamir1,2,3, Ken-Pin Hwang4, Naoyuki Takei5, and Suchandrima Banerjee6
1Electrical and Computer Engineering, The University of Texas at Austin, Austin, TX, United States, 2Diagnostic Medicine, Dell Medical School, The University of Texas at Austin, Austin, TX, United States, 3Oden Institute for Computational Engineering and Sciences, Austin, TX, United States, 4Imaging Physics, MD Anderson Cancer Center, Houston, TX, United States, 5MR Applications and Workflow, GE Healthcare, Hino, Tokyo, Japan, 6MR Applications and Workflow, GE Healthcare, Menlo Park, CA, United States
1Electrical and Computer Engineering, The University of Texas at Austin, Austin, TX, United States, 2Diagnostic Medicine, Dell Medical School, The University of Texas at Austin, Austin, TX, United States, 3Oden Institute for Computational Engineering and Sciences, Austin, TX, United States, 4Imaging Physics, MD Anderson Cancer Center, Houston, TX, United States, 5MR Applications and Workflow, GE Healthcare, Hino, Tokyo, Japan, 6MR Applications and Workflow, GE Healthcare, Menlo Park, CA, United States
Synopsis
Fast, volumetric multi-contrast and quantitative imaging has a broad range of applications, but applying them in 3D remains challenging. Most volumetric approaches rely on gradient-echo-based acquisitions to achieve high scan-efficiency, even though spin-echo imaging provides higher SNR. Here we explore a hybrid acquisition that combines a fast-spin-echo acquisition block with multiple spoiled gradient-echo blocks to acquire spin- and gradient-echo images. We use a shuffled acquisition ordering together with a global subspace constraint and local low rank regularization to accelerate the scan. Following reconstruction, we fit the time series of images to quantitative parameters directly in the subspace using dictionary matching.
Introduction
Multi-contrast imaging forms the backbone of many clinical imaging studies. Recently, there has been a push toward acquiring quantitative data in a highly efficient scan$$$^{1-3}$$$. To increase scan efficiency, these scans typically use 2D imaging in order to benefit from slice interleaving. Extending multi-parameter quantitative imaging to volumetric acquisitions is clinically desirable to obtain isotropic resolution, and a number of methods have been proposed$$$^{4-10}$$$. Spin-echo based imaging is considered the gold standard for quantitative T1 and T2 relaxometry due to its resilience to field inhomogeneity and high SNR. Nonetheless, volumetric relaxometry has traditionally relied on gradient echo (GRE) based acquisitions owing to their high scan efficiency, yet subtle differences in image contrast and quantitative maps are often present between spin and gradient echo. While volumetric FSE provides high quality contrast images, it has traditionally been limited clinically due to T2-decay blurring and low scan efficiency$$$^{11}$$$. Hybrid acquisitions combining an FSE block with a GRE block have been used to obtain multiple images in a single scan while effectively using the scan wait time to increase scan efficiency$$$^{12,13}$$$. In this work we take a similar path and combine a 3D FSE acquisition backbone with a Look Locker$$$^{14}$$$ spoiled gradient echo (SPGRE) during the scan deadtime. In this way, we are able to increase the scan efficiency while retaining a diversity of spin-echo and gradient echo images. We employ a shuffled phase encode ordering and a subspace-based local low rank (LLR) reconstruction$$$^{15}$$$ to resolve images along the full signal evolution curve$$$^{16-18}$$$. Using these images, we solve for quantitative proton density (PD), T1, T2, and B1 with a dictionary-based fit$$$^1$$$.Methods
Pulse Sequence Design. A 3D FSE pulse sequence was previously modified to re-sample phase encodes at different echo times$$$^{17}$$$ and with variable refocusing flip angles$$$^{11}$$$. Following the FSE train with driven equilibrium, we include a 180-degree adiabatic inversion pulse followed by a series of Look-Locker$$$^{14}$$$ SPGRE acquisition blocks (Fig. 1). The sequence timing was simulated using the Extended Phase Graph (EPG) algorithm$$$^{19,20}$$$. Acquisition parameters were empirically chosen to obtain an acceptable tradeoff between scan efficiency, T1- and T2- sensitivity, SNR, and scan time. The first four echoes of each acquisition block were used to acquire auto calibration data for sensitivity map estimation. Variable-density Poisson-disc sampling patterns were prescribed for each echo in one acquisition block, and repeated for the remaining acquisition blocks, resulting in 300 highly under-sampled images along the signal evolution curve.Subspace Design. A temporal subspace was constructed by simulating a dictionary of $$$N=205$$$k signal evolutions uniformly sampled from a grid of T1 (100 ms to 3000 ms, 20 ms resolution), T2 (10 ms to 3000 ms, 5 ms resolution), and B1 scaling values (80% to 120%, 10% resolution) (Fig. 2a). To remove large oscillatory components, each acquisition block was fit to a degree-10 polynomial (Fig. 2b). From this dictionary, a subspace of size $$$K=5$$$ was created through singular value decomposition$$$^{16,17}$$$, representing less than 2% model fitting error (Fig. 2c).
Reconstruction Algorithm. The forward model is $$$\mathbf{y}=\mathbf{Ex}$$$, where $$$\mathbf{x}$$$ is the time series of images along the signal evolution, $$$\mathbf{E}$$$ is the ESPIRiT-based$$$^{21}$$$ sensitivity encoding operator, and $$$\mathbf{y}$$$ are the k-space measurements. The model is relaxed, and the signal is approximated by $$$\mathbf{x}=\mathbf{\Phi\alpha}$$$, where $$$\mathbf{\Phi}$$$ is the pre-determined temporal basis of dimension $$$K$$$ and $$$\alpha$$$ are the temporal image coefficients. The reconstruction, implemented in BART$$$^{22}$$$, is posed as$$\min_{\mathbf{\alpha}}\frac{1}{2}||\mathbf{y}-\mathbf{E\Phi\alpha}||_2^2+\lambda\sum_{\mathbf{r}}||R_{\mathbf{r}}(\mathbf{\alpha})||_*$$LLR regularization was applied to the coefficients to enforce spatio-temporal sparsity$$$^{15}$$$. After reconstruction, the time series of images was obtained through back-projection. Following reconstruction, quantitative T1, T2, and B1 maps were evaluated through dictionary matching directly in the subspace$$$^{1,23}$$$ by projecting the dictionary onto the basis (Fig. 2d).
Experiments. As proof-of-principle, the NIST/ISMRM (CaliberMRI, Boulder CO) phantom was scanned on a 3 Tesla GE Discovery 750W (GE healthcare, Waukesha, WI), with scan parameters shown in Fig. 1c and total scan time 7:44 minutes. An additional scan was performed without shuffling to obtain baseline images, one for each acquisition block.
Results and Discussion
Fig. 3a shows the reconstructed basis coefficient images for one slice from the phantom at full and relative dynamic range. Fig. 3b compares one image from each acquisition block (with and without shuffling). Some residual incoherent aliasing remains, likely due to limitations in sampling pattern and sequence parameter selection. Nonetheless, there is reasonable agreement in image contrast with and without shuffling, as well as increase in image sharpness resulting from resolving the temporal relaxation curve in the former. Fig. 4 shows an animation of the time series of images for three slices from the phantom. Fig. 5 shows PD, T1, T2, and B1 maps resulting from the dictionary fit. Further evaluation of quantitative bias is left for future work.The proposed hybrid acquisition presents a number of opportunities for fast multi-contrast and quantitative imaging, namely due to the combination of spin and gradient echoes with high scan efficiency. However, due to the interplay between the biophysical tissue parameters and the acquisition blocks, careful modeling is needed to obtain an accurate quantitative fit.
Conclusion
We have demonstrated a hybrid, signal evolution-resolved acquisition combining FSE and SPGRE for volumetric multi-contrast and quantitative volumetric imaging.Acknowledgements
We thank Ke Wang for feedback on the subspace design. This work was supported by a seed grant from MD Anderson Cancer Center, Oden Institute for Computational Engineering and Sciences, and the Texas Advanced Computing Center.References
- Ma D, Gulani V, Seiberlich N, et al., Magnetic Resonance Fingerprinting. Nature 495, no. 7440 (2013). doi:10.1038/nature11971.
- Warntjes JBM, Leinhard OD, West J, Lundberg P. Rapid Magnetic Resonance Quantification on the Brain: Optimization for Clinical Usage. Magnetic resonance in medicine 60, no. 2 (2008). doi:10.1002/mrm.21635.
- Wang X, Tan Z, Scholand N, et al., Physics-based Reconstruction Methods for Magnetic Resonance Imaging. arXiv preprint arXiv:2010.01403 (2020).
- Ma D, Jiang Y, Chen Y, et al. Fast 3D magnetic resonance fingerprinting for a whole‐brain coverage. Magnetic resonance in medicine 79.4 (2018): 2190-2197.
- Wang F, Dong Z, Reese TG, et al. Echo planar time‐resolved imaging (EPTI). Magnetic resonance in medicine 81.6 (2019): 3599-3615.
- Dong Z, Wang F, Reese TG, et al. Echo planar time‐resolved imaging with subspace reconstruction and optimized spatiotemporal encoding. Magnetic Resonance in Medicine 84.5 (2020):2442-2455.
- Chaudhari AS, Black MS, Eijgenraam, S, et al., Five‐minute knee MRI for simultaneous morphometry and T2 relaxometry of cartilage and meniscus and for semiquantitative radiological assessment using double‐echo in steady‐state at 3T. Journal of Magnetic Resonance Imaging, 47(5) (2018), 1328-1341.
- Kvernby, S, Warntjes MJB, Haraldsson H, et al., Simultaneous three-dimensional myocardial T1 and T2 mapping in one breath hold with 3D-QALAS. Journal of Cardiovascular Magnetic Resonance 16.1 (2014): 1-14.
- Fujita S, Hagiwara A, Takei N, et al., Accelerated Isotropic Multiparametric Imaging by High Spatial Resolution 3D-QALAS With Compressed Sensing: A Phantom, Volunteer, and Patient Study. Invest Radiol. 2020.
- Keerthivasan, MB, Saranathan M, Johnson K, et al. An efficient 3D stack‐of‐stars turbo spin echo pulse sequence for simultaneous T2‐weighted imaging and T2 mapping. Magnetic resonance in medicine 82.1 (2019): 326-341.
- Busse RF, Hariharan H, Vu A, Brittain JH. Fast Spin Echo Sequences with Very Long Echo Trains: Design of Variable Refocusing Flip Angle Schedules and Generation of Clinical T2 Contrast. Magnetic resonance in medicine 55, no. 5 (2006). doi:10.1002/mrm.20863.
- Li G, M. Zaitsev M, Weigel M, et al., On the feasibility of hybrid acquisition in SPACE. Proc Intl Soc Mag Reson Med 22, Milan, 2014. p. 1467.
- Benkert T, Mugler JP, Rigie DS, et al., Hybrid T2 - and T1 -weighted radial acquisition for free-breathing abdominal examination. Magn Reson Med 2018. DOI: 10.1002/mrm.27200.
- Look DC, Locker DR. "Time saving in measurement of NMR and EPR relaxation times." Review of Scientific Instruments 41.2 (1970): 250-251.
- Trzasko JD, Manduca A. Local versus global low-rank promotion in dynamic MRI series reconstruction. In Proceedings of International Symposium on Magnetic Resonance in Medicine, Vol. 19, Montreal, Quebec, Canada, 2011. p. 4371.
- Huang C, Graff CG, Clarkson EW, et al., T2 Mapping From Highly Undersampled Data by Reconstruction of Principal Component Coefficient Maps Using Compressed Sensing. Magnetic resonance in medicine 67, no. 5 (2012). doi:10.1002/mrm.23128.
- Tamir JI, Uecker M, Chen W, et al., T2 Shuffling: Sharp, Multicontrast, Volumetric Fast Spin-echo Imaging. Magnetic resonance in medicine 77, no. 1 (2017). doi:10.1002/mrm.26102.
- Tamir JI, Taviani V, Vasanawala SS, Lustig M. T1-T2 Shuffling: Multi-Contrast 3D Fast Spin-Echo with T1 and T2 Sensitivity. Proc Intl Soc Mag Reson Med 25, Honolulu, HI, 2017. p. 0451.
- Hennig J. Multiecho imaging sequences with low refocusing flip angles. Journal of Magnetic Resonance (1988) 78.3 (1988): 397-407.
- Weigel M. Extended phase graphs: dephasing, RF pulses, and echoes‐pure and simple. Journal of Magnetic Resonance Imaging 41.2 (2015): 266-295.
- Uecker M, Lai P, Murphy MJ, et al., ESPIRiT-an Eigenvalue Approach to Autocalibrating Parallel MRI: Where SENSE Meets GRAPPA. Magnetic resonance in medicine 71, no. 3 (2014). doi:10.1002/mrm.24751.
- Uecker M, et al., BART Toolbox for Computational Magnetic Resonance Imaging, DOI: 10.5281/zenodo.592960.
- Tamir JI, Ong F, Anand S, et al., Computational MRI With Physics-Based Constraints: Application to Multicontrast and Quantitative Imaging. IEEE Signal Processing Magazine 37.1 (2020): 94-104.
Figures
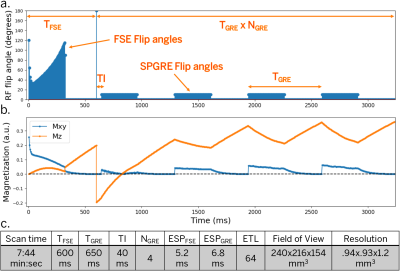
Figure 1. EPG Simulation and scan parameters. (a) RF flip angles (90-degree excitation not shown). (b) Transverse and longitudinal magnetization for T1=1600 ms, T2=80 ms (after arriving at a stable equilibrium magnetization). (c) Scan parameters for simulation and phantom experiments. The first acquisition block uses an FSE train with non-selective variable refocusing flip angles and a fast recovery tip-up pulse. After an adiabatic inversion pulse, a series of SPGRE blocks are played in sequence.
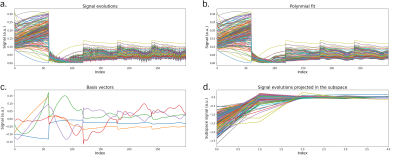
Figure 2. (a) A dictionary of signal evolutions was simulated according to the sequence parameters in Fig. 1c. (b) To remove highly oscillatory components, each acquisition block of each signal was fit to a degree-10 polynomial. (c) After, a basis of size K=5 was generated using singular value decomposition. (d) The dictionary is projected onto the subspace for quantitative fitting of the reconstructed subspace coefficient images.
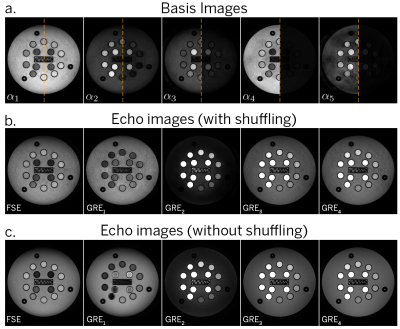
Figure 3. (a) Basis coefficient images from the multi-contrast shuffling reconstruction, shown at full and relative dynamic range). (b) Multi-contrast echoes after back-projection, showing one echo from each acquisition block (300 total images). (c) Multi-contrast echoes from a non-shuffled acquisition (5 total images).

Figure 4. Animated gif of the reconstructed time series of images at three different slices in the ISMRM-NIST phantom, corresponding to the three plates of contrast spheres. In total, a time series of 300 images are reconstructed.
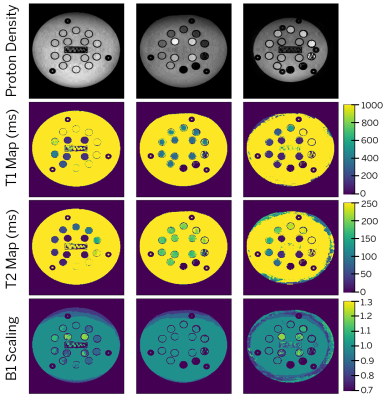
Figure 5. Results of quantitative mapping for the three slices from Fig. 4 using dictionary fitting. From top to bottom: proton density, T1 map (ms), T2 map (ms) and B1 scaling.