Introduction

T₂- and diffusion-weighted (DW) MR images are essential in protocols for breast, prostate, or head and neck cancer^1–3. The serial acquisition of these two MR contrasts can be time-consuming, and a co-registration is difficult, as DWI is typically using echo-planar acquisitions, that are prone to image distortion, whereas T₂w protocols often utilize fast spin echo sequences with an excellent geometric accuracy. To overcome some of these problems, several pulse sequences have been proposed to acquire diffusion ADC and T₂-maps in a single acquisition^4–7. Here, we present a new radial fast spin echo (FSE) sequence that interleaves diffusion weighting and multi-echo acquisition in an echo train, and uses a compressed sensing reconstruction to accelerate the acquisition.

Materials and Methods

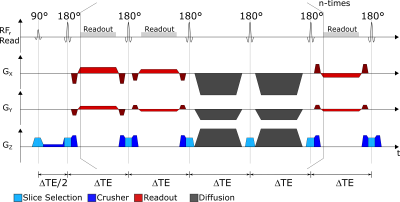
Pulse-Sequence
A radial FSE sequence for simultaneous T₂ and ADC measurements was implemented which employs a spin echo train with multiple acquisitions that is interleaved by diffusion sensitization blocks. Thus, each echo train acquires a unique set of radial k-space spokes with different echo times ΔTE and b-values (Figure 1). For identical ΔTE-b-pairs, the echo train is measured repeatedly to sample additional k-space spokes. Furthermore, the echo spacing ΔTE is varied to acquire additional ΔTE-b-pairs. Radial spokes are acquired with a Golden Angle increment so that no spoke is measured more than once.

Reconstruction
To reconstruct the parameter maps of T₂ and D (i.e., the ADC), a compressed sensing reconstruction algorithm was implemented (8):
$$I_{\text{Recon}}=\arg\underset{x}{\min}\left(\lVert\mathcal{F}\left(\mathcal{F}^{-1}\left(x\right)-y\right)\rVert_2+\lambda\,\lvert\text{TV}\left(x\right)\rvert_1\right)$$

where $$$x$$$ is the current image estimate, $$$y$$$ the measured raw-data, and $$$\mathcal{F\left(x\right)}$$$ and $$$\mathcal{F}^{-1}\left(x\right)$$$ are the non-uniform (inverse) Fourier transforms, $$$\lambda$$$ is an adjustable weight and $$$\text{TV}\left(x\right)$$$ the total variation in both spatial dimensions. The optimization problem is solved using conjugate gradients. Additionally, the signal equation
$$S=S_0e^{-bD}e^{-\frac{t}{T_2}}$$
is incorporated as prior knowledge in the iterative reconstruction algorithm. After each iteration, the current estimate $$$x$$$ is replaced by $$$x^\prime$$$, with
$$x^\prime=\mathcal{E}^{-1}\left(\mathcal{E}\left(x\right)\right)e^{-i\phi\left(x\right)}$$
Here, $$$\mathcal{E}\left(x\right)$$$ is the double exponential pixelwise least squares fit of $$$x$$$, yielding the parameter maps $$$S_0$$$, $$$D$$$, and $$$T_2$$$. $$$\mathcal{E}^{-1}\left(x\right)$$$ is the inverse function that generates signal intensities $$$S\left(b,D,t,T_2\right)$$$ from the parameter maps. Since $$$\mathcal{E}$$$ is only defined on absolute values, the phase $$$\phi\left(x\right)$$$ is added from the original images.

Simulation
Phantom data were simulated with three different ΔTE = [11, 11.5, 12] ms, and an echotrain with 15 readouts and diffusion blocks after 3 readouts each was used resulting in 45 TE between 11–288 ms and b-values between 0-831 s/mm². To assess the robustness against noise, complex Gaussian random noise (SNR=25 and 50) was added to a fully sampled data set.

Phantom Measurements
The sequence was implemented on a clinical 3T MRI system (PRISMA, Siemens, Erlangen, Germany) using the sequence prototyping environment PulseSeq⁹. Phantom images were acquired with the same parameters as in the simulation. For reference measurements, a standard diffusion weighted EPI with b=[50, 400, 800] s/mm² and a FSE sequence with 32 echoes between 13-442 ms were used.

Results

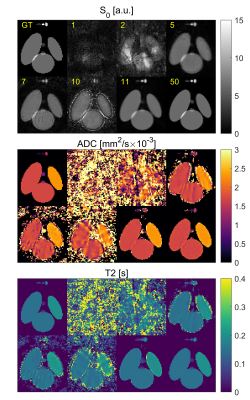
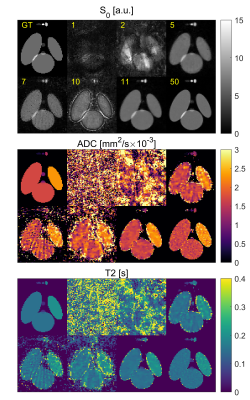
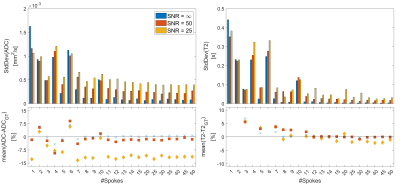
Simulation
Figure 2 shows the simulation results for a varying number of spokes for infinite SNR. Robust reconstruction with less than 0.85% deviation in ADC and T₂ can be achieved with 11 spokes or more. When noise is added (Figure 3) a similar behavior is seen: T₂ deviates at most by 1.9/2.2% for SNR of 50/25 for 11 or more spokes, whereas the ADC shows a stronger bias of 2.8/12.6% (Figure 4). The standard deviation of estimated ADC values does not decrease significantly if more than 25 spokes are acquired, and never falls below [0.10, 0.27, 0.40]·10^-3mm²/s for SNRs of [∞, 50, 25]. Similarly, the T₂ standard deviations never fall below [5.2, 18.9, 56] ms with the smallest deviation at 40 spokes.

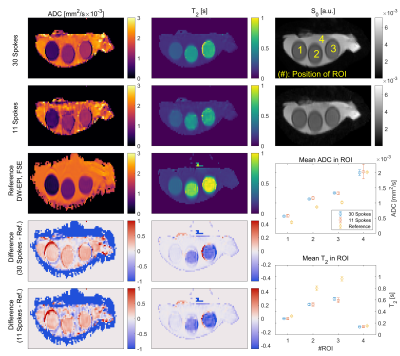
Phantom Measurement
In the phantom measurements for 11/30 spokes per ΔTE-b-pair (Figure 5), ADC values agree with the DW-EPI measurement for the highest ADC, but show a systematic deviation of up to 0.26·10^-3 mm²/s towards smaller ADCs. Lower diffusion values show smaller signal variations (±0.21·10^-3 vs. ±0.96·10^-3 mm²/s for ADC≈2 mm²/s). The T₂ measurement shows best agreement with the reference measurement for T₂<0.4s. Reconstruction with only 11 instead of 30 spokes produces consistent results in the ROI-based analysis (Figure 5). ADC in all ROIs and T₂ based values in ROIs 2 and 3 show a significantly larger standard deviation compared to the reconstruction based on 30 spokes.

Discussion and Conclusion

In this work we proposed a sequence to measure ADC and T₂ simultaneously. With the proposed parameters (11 spokes per ΔTE-b-pair, ΔTE = [11, 11.5, 12] ms and 4 diffusion blocks) and a TR of 5 s, ADC and T₂ maps for 18 slices can be measured in less than one minute. Since the b-value gradually increases over the echotrain, strong motion related random phase fluctuations are less probable, which allows the use of a multi-excitation procedure. A good slice profile should be used, as stimulated echoes can arise from imperfect excitation/refocusing which manifest in severe artifacts, thereby violating the model assumption in the reconstruction. The sequence circumvents distortion artifacts typical for EPI-based sequences by high bandwidths and the radial acquisition scheme.

Acknowledgements

No acknowledgement found.