4067
Acceleration of high-resolution proximal femur MRI using compressive sensing and sparsity in a retrospective study1Bioengineering, University of Pennsylvania, Philadelphia, PA, United States, 2Radiology, University of Pennsylvania, Philadelphia, PA, United States, 3Radiology, Center for Biomedical Imaging, New York University, New York, NY, United States, 4Orthopaedic Surgery, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PA, United States
Synopsis
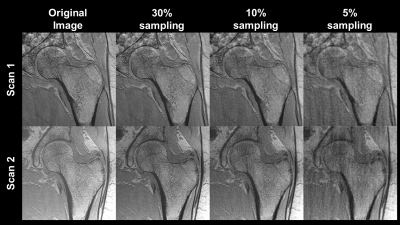
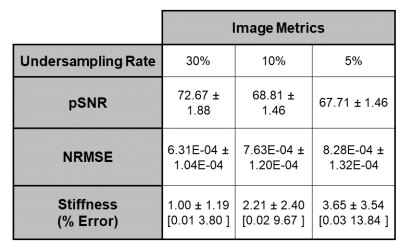
Retrospective compressive sensing techniques demonstrate promise accelerating acquisition of high-resolution images of the femur while maintaining sufficient image quality to assess fracture risk. While the trabecular bone microstructure was preserved at an undersampling rate of 30%, lower sampling rates of 10% and 5% exhibited visually apparent artifacts and image degradation. Similarly, bone stiffness at 30% resembled fully sampled data but the error increased as sampling rate decreased. Nevertheless, the results show that compressive sensing is a promising candidate for accelerating the acquisition rate, and further prospective studies are needed to further validate this finding.
INTRODUCTION
Hip fractures pose a sizable danger to affected patients. Within a year of the fracture event, 50% of patients cannot walk and 20-30% do not survive[1,2]. Existing clinical methods, which rely on dual energy X-ray absorptiometry (DXA) evaluation of mineral density, have high specificity but low sensitivity (<50%) for predicting fracture[3]. Recent MR advances have enabled direct imaging of trabecular microstructure at the hip[4-7]. Finite element analysis (FEA) of high-resolution proximal femur images have been shown to accurately simulate bone strength as a means of assessing mechanical competence[7,8].However, the spoiled gradient-recalled (SPGR) sequence used to acquire these microarchitectural images in vivo requires approximately 16 minutes. For clinical viability, the acquisition time for these high-resolution images should be as short as possible. In order to further push the envelope and reduce scan times, this work investigated the feasibility of performing a sparse undersampling and compressive sensing (CS)[9] method to reconstruct high-resolution proximal femur images, as well as the effect of undersampling rates on bone stiffness predictions.
METHODS
(1) CS allows for image reconstruction of highly undersampled k-space provided that there is a pseudorandom sampling method, the image is sparse or compressible in some transformation domain[9,10], and that prior information can be added to the optimization[9]. Here we employ the Daubechies discrete wavelet transform[11] as the sparsifying transform since MR images are known to be compressible in the wavelet domain[12-14]. Once in the wavelet domain, the absolute value of each voxel was computed, and the indices of the highest 15% of signal values were kept. Signal values at all other indices were set to zero, and the inverse discrete wavelet transform was taken of the remaining data. Successful recovery of a compressed image indicated potential for the implementation of compressive sensing techniques.(2) Retrospective undersampling was performed via Monte Carlo method described previously[9] with a binomial probability mass function centered at the origin of k-space. This emphasized the selection of low-frequency information which have higher magnitude Fourier coefficients. With this sampling scheme, 49 in vivo proximal femora MR images from a previous study[6] (Figure 3) which were already complex coil-combined were retrospectively undersampled to test the efficacy of CS methods for high-resolution bone imaging. Images of dimensions 512x512x60 were each undersampled at rates of 5%, 10% and 30% (i.e. 95%, 90%, and 70% of k-space data points were discarded for each image in each of these respective datasets), as seen in Figure 1. The scanner and sequence parameters for data acquisition of the original MR images are shown in Figure 2. The alternating direction method of multipliers (ADMM) was used to solve the following constraint problem:
$$\min_{\gamma}\frac{1}{2}||y - D \mathcal{F} \gamma||^2 + \lambda||\Psi \gamma||_1. $$
$$$y$$$ are the measurements in k-space, $$$\gamma$$$ is the image solution, $$$D$$$ is the downsampling operator, $$$\mathcal{F}$$$ is the 3-D discrete Fourier transform, $$$\Psi$$$ is the 3-D discrete wavelet transform, and $$$\lambda$$$ is a weighting parameter for the ADMM algorithm[10,15]. 10 iterations of ADMM were used, with $$$\lambda = 0.5$$$.
(3) Proximal femur stiffness was simulated using linear FEA methods to simulate a sideways fall fracture loading condition, as described previously[8]. Briefly, the images were manually segmented at the periosteal boundary and the voxel intensities were scaled to values representing material compositions in the range between pure bone marrow and pure cortical bone. Signal intensity was then inverted and scaled linearly between 0 and 100, with 100 assumed to be pure bone at 15 GPa and 0 corresponding to pure marrow at 0 GPa. Acetabular segmentations created boundary conditions around the femoral neck and additional force pads were added to the lesser trochanter[7]. Incremental strain was then applied to simulate a typical fall to the side[8].
RESULTS
At an undersampling rate of 30%, the model produced reliable reconstructions which preserved the majority of the trabecular microstructure. Only minor reductions in SNR and blurring along the cortical shaft can be seen. In contrast, at 10% and 5% undersampling rates, the trabecular microstructure is greatly obscured and major artifacts are present (Figure 3). Table 4 details image quantitative metrics and bone stiffness predictions. Similar to the image quality, the bone stiffness simulations perform best at 30% and decrease as the undersampling rate increases.DISCUSSION
The present abstract comprises the preliminary results that CS methods may be useful at reconstructing high-resolution bone MR scans which are sampled far below the Nyquist criterion. Image metrics and bone stiffness predictions were only marginally affected by large undersampling rates. However, it is important to note that these retrospective analyses were made on k-space data which were already complex coil-combined. It is likely that the addition of multiple coils as well as prospective undersampling will increase model complexity and reduce SNR and the reconstruction efficacy and thus the results should be viewed as an upper bound for what is possible for CS methods. Nevertheless, the results are promising and warrant further investigation.CONCLUSION
This study suggests that compressed sensing reconstruction methods may be useful in accelerating high-resolution proximal femur imaging. Ongoing work will extend the model to work for multi-coil parallel imaging acquisition and prospectively evaluate the effects of compressive sensing undersampling methods on bone strength predictions.Acknowledgements
NIH R01 AR068382, R01 AR076392, T32 EB009384References
1. Brauer, C.A., M. Coca-Perraillon, D.M. Cutler, and A.B. Rosen, Incidence and mortality of hip fractures in the United States. Jama, 2009. 302(14): p. 1573-9.
2. Magaziner, J., L. Fredman, W. Hawkes, J.R. Hebel, S. Zimmerman, D.L. Orwig, and L. Wehren, Changes in functional status attributable to hip fracture: a comparison of hip fracture patients to community-dwelling aged. Am J Epidemiol, 2003. 157(11): p. 1023-31.
3. Marshall, D., O. Johnell, and H. Wedel, Meta-analysis of how well measures of bone mineral density predict occurrence of osteoporotic fractures. Bmj, 1996. 312(7041): p. 1254-9.
4. Krug, R., S. Banerjee, E.T. Han, D.C. Newitt, T.M. Link, and S. Majumdar, Feasibility of in vivo structural analysis of high-resolution magnetic resonance images of the proximal femur. Osteoporos Int, 2005. 16(11): p. 1307-14.
5. Han, M., K. Chiba, S. Banerjee, J. Carballido-Gamio, and R. Krug, Variable flip angle three-dimensional fast spin-echo sequence combined with outer volume suppression for imaging trabecular bone structure of the proximal femur. Journal of magnetic resonance imaging : JMRI, 2015. 41(5): p. 1300-1310.
6. Chang, G., S. Honig, R. Brown, C.M. Deniz, K.A. Egol, J.S. Babb, R.R. Regatte, and C.S. Rajapakse, Finite element analysis applied to 3-T MR imaging of proximal femur microarchitecture: lower bone strength in patients with fragility fractures compared with control subjects. Radiology, 2014. 272(2): p. 464-74.
7. Rajapakse, C.S., A. Hotca, B.T. Newman, A. Ramme, S. Vira, E.A. Kobe, R. Miller, S. Honig, and G. Chang, Patient-specific Hip Fracture Strength Assessment with Microstructural MR Imaging-based Finite Element Modeling. Radiology, 2017. 283(3): p. 854-861.
8. Rajapakse, C.S., A.R. Farid, D.C. Kargilis, B.C. Jones, J.S. Lee, A.J. Johncola, A.S. Batzdorf, S.S. Shetye, M.W. Hast, and G. Chang, MRI-based assessment of proximal femur strength compared to mechanical testing. Bone, 2020. 133: p. 115227.
9. Lustig, M., D. Donoho, and J.M. Pauly, Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine, 2007. 58(6): p. 1182-1195.
10. Ye, J.C., Compressed sensing MRI: a review from signal processing perspective. BMC Biomedical Engineering, 2019. 1(1): p. 8.
11. Lee, G.R., R. Gommers, F. Waselewski, K. Wolfhart, and A. O'Leary, PyWavelets: A Python package for wavelet analysis. Journal of Open Source Software, 2019. 4(36): p. 1237.
12. Ma, J., M. März, S. Funk, J. Schulz-Menger, G. Kutyniok, T. Schaeffter, and C. Kolbitsch, Shearlet-based compressed sensing for fast 3D cardiac MR imaging using iterative reweighting. Phys Med Biol, 2018. 63(23): p. 235004.
13. Zibetti, M.V.W., A. Sharafi, R. Otazo, and R.R. Regatte, Compressed sensing acceleration of biexponential 3D-T(1ρ) relaxation mapping of knee cartilage. Magn Reson Med, 2019. 81(2): p. 863-880.
14. Li, Q., X. Qu, Y. Liu, D. Guo, Z. Lai, J. Ye, and Z. Chen, Accelerating patch-based directional wavelets with multicore parallel computing in compressed sensing MRI. Magn Reson Imaging, 2015. 33(5): p. 649-58.
15. Wang, Y., J. Yang, W. Yin, and Y. Zhang, A New Alternating Minimization Algorithm for Total Variation Image Reconstruction. SIAM Journal on Imaging Sciences, 2008. 1(3): p. 248-272.
Figures