Introduction

Permanent-magnet-array(PMA)-based portable MRI systems have obtaining increasing attention recently[1-3]. Permanent magnet is a good option to supply the static magnetic field(B₀+gradient fields, with or without gradient coils) for the portability of MRI because it doesn’t need power or cooling and are low-cost. However, due to the use of permanent magnets, the field strength is low, the field pattern may not be linear, and the homogeneity leads to a wide system working bandwidth. Therefore, a PMA has different requirements on other parts of the system and it affects the image quality differently compared to a conventional system. For example, a low field strength and a high inhomogeneity require the RF coil to have a high B₁ sensitivity and a wide bandwidth. The field is not homogeneous thus it does not work with conventional linear gradient coils (new gradient-coils can be an option to have a desired pattern) and it takes localized k-spaces to analyze the quality of encoding.

A digital version of such a system, a digital-twin, that consists of different simulators connecting different parts of the system(PMA, RF-coil, and gradient-coils, etc.) is critical to design, optimize, hardware debug and calibrate, and evaluate such a system at a system and a sub-system level. Meanwhile, it will facilitate the design and development of a sub-system without building a whole system. Here, we present the development of such a digital-twin.

Method

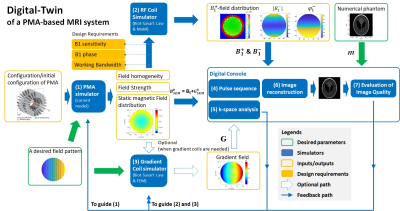
Fig.1 shows the components of the digital-twin and the key inputs/outputs between the simulators. The PMA-simulator takes the characteristics(e.g.magnet grades) and configuration of magnet blocks(e.g.dimension, location, and orientation) as inputs and generate the spatial encoding magnetic field, B^μ_SEM=B₀+G^μ_SEM in a defined field-of-view(FoV). The homogeneity, strength, and distributions of the calculated are the outputs. The former two outputs are translated into the requirements on B₁ sensitivity, B₁ phase, and working bandwidth, entering the RF-coil-simulator which designs transmit- and receive-coils with the required field strengths, patterns, and phase distribution. Meanwhile, when gradient-coils are added, the output field-distribution is delivered to the gradient-coil-simulator to guide the designs for a desired field-distribution.

When B^μ_SEM, B₁, and G(optional) are ready, together with the numerical phantom, they enter the digital-console which consists of the simulators for pulse sequence, k-space analysis, image reconstruction, and image quality evaluations. Both the k-space analysis(simulator-5) and the image quality evaluation(simulator-7) can be feedback for further design and optimizations(detailed in Fig.2).

For the PMA simulator, magnet blocks that are available off-the-shelf and current model were used, and the acceleration of calculations was proposed(details reported in another submitted abstract). For the RF-coil-simulator, it includes both Biot-Savart-Law(for coils with wires) or Method of Moments(MoM)(for coils with planar structures). It can accommodate the designs for Transmit-Array-Spatial-Encoding(TRASE) and Sensitivity-Encoding(SENSE)-coils. For the gradient-coil-simulator, there are options of using Biot-Savart-law and finite-element-method(FEM). The k-space analysis includes global and local ones, depending on the gradients for the encoding field. The image reconstruction includes both FFT and generalized reconstructions, depending on the linearity of the encoding gradients.

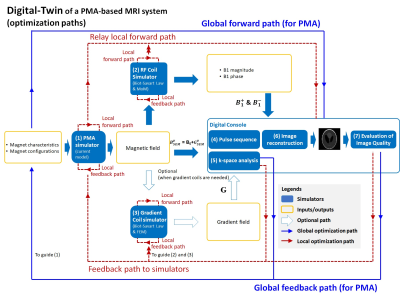
The proposed digital-twin supports both global- and local-optimizations, as indicated by the blue line and red line in Fig.2, respectively. For the global-optimization for PMA, the feedback is fed to guide the magnet characteristics and configuration for optimization. For local-optimizations, the feedback information is fed to each simulator as a goal for the simulator for further designs and optimizations before carrying forward. For both optimizations, different optimization algorithms can be applied.

Results & Discussions

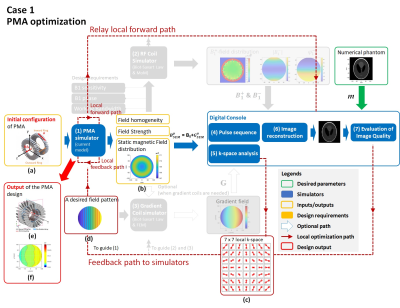
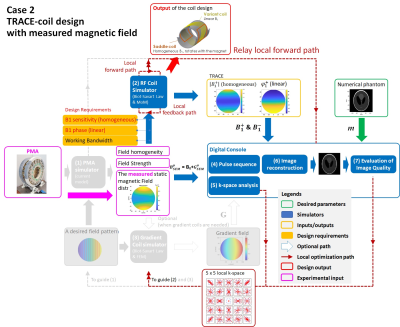
Case-1 is the local PMA optimization using the proposed digital-twin(Fig.3). It starts with an initial discretized inward-outward-ring-array(Fig.3a, 48blocks). Calculation of B^μ_SEM was done in the PMA-simulator(28.4seconds/simulation). The calculated field has a concentric pattern(Fig.3b). When this field is used for signal encoding with mechanical rotation[4-5], it entered the digital-console where image reconstruction(simulation-7) and k-space analysis(simulation-5) were performed when a typical CPMG pulse sequence was performed. As the gradient is non-linear, local k-space(Fig.3c) was analyzed where the analysis was feedback to the PMA-simulator to guide the optimization. In this example, a linear pattern along the horizontal direction(Fig.3d) was concluded to be the targeted pattern based on the local k-space analysis and input to the local-optimizer of the PMA-simulator. Genetic algorithm(GA) was used as the optimization algorithm of this simulator which led to an output design with 120blocks including shimming and gradient blocks(Fig.3e) and a field pattern that is close to linear(Fig.3f).

The sub-system of the digital-twin can be replaced by measurement data for the designs of other sub-systems. Fig.4 shows an example of the design of a TRACE-coil when the measured B^μ_SEM of a Halbach-array was used to replace the PMA-simulator.

Besides design and optimizations of a PMA system, the proposed digital-twin serves as a starting point for hardware debugging and calibration for each component and the connections between two successive ones. It helps to evaluate the performance of each component and the overall one, which enables a coordination of the design at a system level.

Conclusion

The proposed digital-twin of a PMA-based MRI system offers a platform to design and optimize such a system at both a sub-system and a system level. It can provide guidance to hardware debug and calibration, and evaluation. It can be used at different development stages of such a system.

Acknowledgements

The authors would like to thank Professor Feng Liu from University of Queensland (Australia) for the discussions on the gradient simulator.