4003
Regional Susceptibility Reconstruction Improves Artifact Incidence and Error in Quantitative Susceptibility Mapping through POSSUM1Cornell University, New York City, NY, United States, 2Weill Cornell Medical College, New York City, NY, United States
Synopsis
Quantitative susceptibility mapping methods that selectively mask based on susceptibility thresholds and do regional reconstructions have been introduced to reduce shadowing artifacts when dealing with a large dynamic susceptibility range within the image. Here, we combine this technique with total field reconstructions, which have been shown to reduce errors resulting from incomplete background field removal. Reduced errors and shadow artifacts are demonstrated when compared to prior techniques.
Summary
A quantitative susceptibility mapping method is proposed that combines regional mapping with total field inversion for improved error and artifact reduction.Synopsis
Quantitative susceptibility mapping methods that selectively mask based on susceptibility thresholds and do regional reconstructions have been introduced to reduce shadowing artifacts when dealing with a large dynamic susceptibility range within the image. Here, we combine this technique with total field reconstructions, which have been shown to reduce errors resulting from incomplete background field removal. Reduced errors and shadow artifacts are demonstrated when compared to prior techniques.Introduction
Quantitative Susceptibility Mapping (QSM) allows obtaining the tissue magnetic susceptibility map from a gradient echo MRI data acquisition. The range of susceptibility values can vary widely over the field of view. For example, healthy brains have susceptibilities on the order of -0.1 to 0.3 ppm and even higher for pathological case. The dipole inversion in QSM is ill-posed and may lead to streaking and shadowing artifacts near sources of high susceptibility. In order to suppress these artifacts, regional susceptibility mapping methods have been proposed that treat low and high susceptibility regions differently, such as STAR QSM and Superposed QSM 1,2. In Superposed QSM, the low susceptibility mask is obtained by thresholding the extracted brain mask, followed by background field removal and local field inversion. Errors in the background removal that propagate into the results of the local field inversion may be overcome by using total field inversion methods3,4,5. In this study, we propose to perform regional mapping by first adding a separate reconstruction for the high susceptibility region, and second using total field inversion. The resulting method is called Part-of-Tissue Optimization of Susceptibility Sources Utilizing Masking, or POSSUM. Feasibility and performance of this method is shown in numerical phantom simulations and COSMOS data.Methods
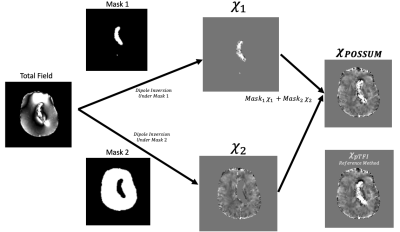
In POSSUM, a susceptibility map in a mask $$$M$$$ is computed by combining two susceptibility reconstructions. Each reconstruction is obtained using separate masks for high ($$$M_H$$$) and low ($$$M_L$$$) susceptibility, which form a partition of $$$M$$$ and were obtained by segmenting an initial susceptibility reconstruction (Figure 1): $$ χ^∗=∑_{i=L,H} M_i argmin_{χ_i } 0.5 ‖M_i w(f-d∗Pχ_i )‖_2^2+λ‖M_i M_G ∇Pχ_i ‖_1 $$, (1)with P a preconditioner4. POSSUM was performed on the following data sets, a numerical brain phantom with a simulated hemorrhage, a multiple orientation data set for using the COSMOS reconstruction as ground truth, and 20 clinical cases, 12 with and 8 without cerebral hemorrhage.For all data, an initial reconstruction was performed using MEDI3 (λ = 0.001). From this reconstruction, a $$$M_2 $$$(which may be called $$$ M_L$$$) was obtained by selecting all voxels in $$$M$$$ below 0.3ppm, followed by an erosion using a 3mm radius spherical kernel. $$$M_1$$$ (which may be called $$$M_H$$$ ) was then $$$M$$$ \ $$$M_2$$$. The reconstruction for each mask (Eq. 1) was done using pTFI with P = 30, λ = 0.001.3,4 Masks are only applied at the field to susceptibility source dipole inversion step, as outlined in Figure 1. For comparison, PDF+MEDI3 (λ = 0.001, no masking), pTFI4 (P = 30, λ = 0.001, no masking), and Superposed QSM2 was computed as well. In Superposed QSM, a second reconstruction is only performed for $$$M_L$$$. For each reconstruction, a shadow index was defined to quantify the degree the shadowing. It was computed as the standard deviation of the low frequency content of susceptibility values < 0.1 ppm, with the low frequency content computed with the SMV kernel of 1 mm.5Results
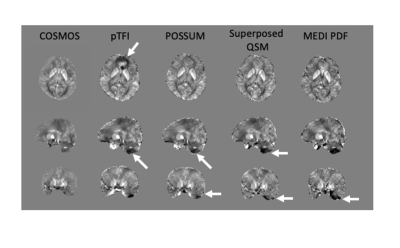
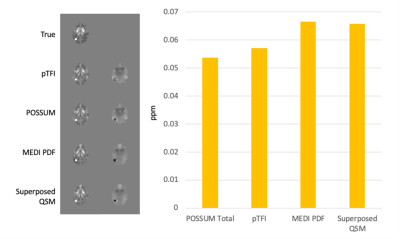
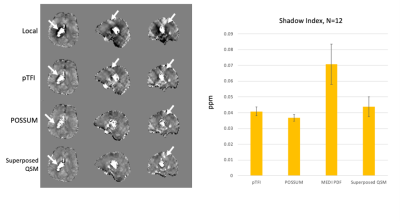
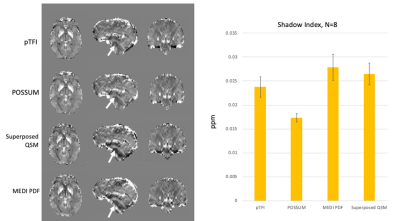
Figure 2 shows a comparison of the COSMOS, pTFI, POSSUM, and Superposed QSM results in a healthy subject in an axial, sagittal and coronal slice. There is a visible artifact reduction compared to pTFI for both Superposed QSM and POSSUM, but POSSUM shows the lowest RMSE error at 0.0342, 0.0361, and 0.039, 0.041 for POSSUM, Superposed QSM, pTFI, and MEDI PDF respectively. Figure 3 shows the result in the numerical brain phantom. Figure 4 shows the results in the case of an intracerebral hemorrhage. POSSUM and Superposed QSM show a higher suppression of shadowing artifacts surrounding the hemorrhage. This is reflected in a lower shadow index in Figure 4b where 12 cases are analyzed, with POSSUM being slightly more effective. Figure 5 shows the results in a clinical case without intracerebral hemorrhage. Streaking and shadow artifacts are visibly reduced with POSSUM. This is reflected in a lower shadow index in Figure 5b compared to the other methods.Conclusions and Future Directions
POSSUM demonstrates improved artifact reduction when compared to prior methods. Preliminary data not shown here shows a threshold of susceptibility at 0.05 ppm is effective at suppressing shadows in non-hemorrhage cases. Future directions include extending the use of POSSUM to whole head reconstruction, larger ranges of thresholds tested, further numerical phantom and ground truth evaluation, and automation of masking thresholds.Acknowledgements
No acknowledgement found.References
1. Wei, H., Dibb, R., Zhou, Y., Sun, Y., Xu, J., Wang, N. and Liu, C., 2015. Streaking artifact reduction for quantitative susceptibility mapping of sources with large dynamic range. NMR in Biomedicine, 28(10), p.1294-1303.2.
2. Sun, H., Kate, M., Gioia, L.C., Emery, D.J., Butcher, K. and Wilman, A.H., 2016. Quantitative susceptibility mapping using a superposed dipole inversion method: application to intracranial hemorrhage. Magnetic resonance in medicine, 76(3), p.781-791.3.
3. Liu, T., Wisnieff, C., Lou, M., Chen, W., Spincemaille, P. and Wang, Y., 2013. Nonlinear formulation of the magnetic field to source relationship for robust quantitative susceptibility mapping. Magnetic resonance in medicine, 69(2), p.467-476.
4. Z. Liu, Y. Kee, D. Zhou, Y. Wang, and P. Spincemaille, “Preconditioned total field inversion (TFI) method for quantitative susceptibility mapping,” Magn. Reson. Med., 78(1), p. 303–315, 2017.
5. P. S. Balasubramanian, P. Spincemaille, L. Guo, W. Huang, I. Kovanlikaya, and Y. Wang, “Spatially adaptive regularization in Total Field Inversion for quantitative susceptibility mapping,” iScience, 23(10), p. 101553, 2020.
Figures