3984
Non-regularized Dipole Inversion with streaking suppression via L1-norm optimization
Mathias Gabriel Lambert1,2,3, Cristian Tejos1,2,3, and Carlos Milovic4
1Department of Electrical Engineering, Pontificia Universidad Católica de Chile, Santiago, Chile, 2Biomedical Imaging Center, Pontificia Universidad Católica de Chile, Santiago, Chile, 3Millennium Nucleus for Cardiovascular Magnetic Resonance, Santiago, Chile, 4Department of Medical Physics and Biomedical Engineering, University College London, London, United Kingdom
1Department of Electrical Engineering, Pontificia Universidad Católica de Chile, Santiago, Chile, 2Biomedical Imaging Center, Pontificia Universidad Católica de Chile, Santiago, Chile, 3Millennium Nucleus for Cardiovascular Magnetic Resonance, Santiago, Chile, 4Department of Medical Physics and Biomedical Engineering, University College London, London, United Kingdom
Synopsis
Non-regularized QSM reconstructions are feasible by stopping gradient descent methods before they diverge. These methods consume less computation time, while avoiding the time required for parameter selection. In this work we present a linear dipole inversion method without regularization that uses the L1-norm in a proximal step to prevent streaking propagation and present more robustness against phase outliers. Compared to the Nonlinear Dipole Inversion method, our implementation achieved lower RMSE scores in phantom experiments and in vivo reconstructions with fewer artifacts.
Introduction
Quantitative susceptibility mapping (QSM) is typically performed by minimizing a functional that consists of two terms: a regularizer and data fidelity. These methods require fine-tuning the parameters associated with the regularization terms. Recently, a non-linear inversion method (Nonlinear Dipole Inversion, NDI)1 was presented with similar in vivo results as those obtained with state-of-the-art methods such as MEDI2 and FANSI3. When used with an early stopping the algorithm, the NDI approach can perform dipole inversions without a regularizer. Nevertheless, NDI is prone to noise amplification, and is susceptible to strong streaking artifacts. In parallel, L1-norm data fidelity terms have been successfully used in conjunction with the Total Variation regularization4 to suppress streaking artifacts in QSM. Here, we present a robust and fast non-regularized linear method that uses a L1-norm data fidelity term to prevent streaking artifact propagation.Methods
We propose to solve the dipole inversion problem by formulating the QSM functional using a L1-norm (nDI-L1) data fidelity term (without regularization):$$ \underset{\chi}{\text{argmin}}\left\Vert w\left(F^{H}DF\chi-\phi\right)\right\Vert_1 $$
where $$$F$$$ is the Fourier transform with its inverse $$$F^H$$$, $$$D$$$ is the dipole kernel5,6, $$$\phi$$$ is the tissue phase, $$$\chi$$$ is the susceptibility distribution, $$$w$$$ is a magnitude-based weight or ROI binary mask.
To solve this functional we use the auxiliary variable $$$ z=\left(F^{H}DF\chi-\phi\right) $$$ to augment the functional in a proximal framework:
$$ \underset{\chi}{\text{argmin}}\left\Vert w\cdot z\right\Vert _{1}+\frac{\lambda}{2}\left\Vert \left(F^{H}DF\chi-\phi\right)-z\right\Vert _{2}^{2} $$
The solution scheme is to employ gradient descent for the $$$\chi$$$ sub-problem and a proximal step for $$$z$$$:
$$ \chi_{k+1}=\chi_{k}-\tau\cdot F^{H}D^{H}F\left(\left(F^{H}DF\chi-\phi\right)-z\right) $$
$$z_{k+1}=\max\left(\left|F^{H}DF\chi-\phi\right|-\frac{w}{\lambda},\;0\right)\cdot\text{sign}\left(F^{H}DF\chi-\phi\right)$$
where $$$\tau$$$ is the gradient step size and $$$\lambda$$$ is a Lagrangian weight that acts as the L1 proximal soft-thresholding parameter.
Instead of a fixed $$$\lambda$$$ value, we $$$\lambda$$$ iteratively update $$$\lambda$$$ to threshold a given percentage (5%) of the discrepancy between the input data and the proposed solution (cut-off ratio). The gradient step size $$$\tau$$$ is set to 2. As in the NDI algorithm, the number of iterations is the most critical parameter.
We compared the proposed method with NDI in the following experiments:·
- COSMOS7 forward simulations: From a COSMOS brain reconstruction (2016 QSM challenge dataset)8 we synthetized the local phase and added complex noise to the complex image (SNR=100). In addition, two simulated lesions were added, one paramagnetic (-0.55 ppm) and one diamagnetic (0.3 ppm), to mimic highly noisy phase inconsistencies. We tested the performance of the reconstruction using $$$w=\text{magn}$$$ and $$$w=\text{mask}$$$ as weighting methods.
- SIM2SNR1: Using SIM2SNR1 dataset (2019 QSM challenge)9,10 we compared the performance using the official metrics, plus HFEN11 and XSIM12. We used the provided frequency map data and the masked magnitude data as weight. We zero-padded the field map to 256x256x256 voxels.
- IN-VIVO: Phillips Ingenia 3T. TGE sequence, voxel size: 0.59x0.59x1mm, TR/TE/ΔTE=44/7.2/6.2ms, 5 echoes, bandwidth 550.5 Hz. We perform Laplacian phase unwrapping13 and background field removal using LBV14 and VSHARP15.
Results
Figure 1 shows the results using the COSMOS-brain example. For $$$w=\text{magn}$$$. nDI-L1 took 12.2 seconds and performed 31 iterations. NDI took 45.5 seconds and performed 191 iterations. For $$$w=\text{mask}$$$. nDI-L1 took 9.1 seconds and performed 24 iterations. NDI took 3.3 seconds and performed 13 iterations. nDI-L1 achieved better RMSE scores and it is evident that nDI-L1 manages to effectively reduce streaking artifacts surrounding the lesions. The nDI-L1 reconstruction has a less smooth appearance than NDI reconstruction, in which a better definition of the vein is observed.Figure 2 shows the optimal (RMSE-based) reconstruction and metrics of the SIM2SNR1 dataset. nDI-L1 took 45.3 seconds and performed 26 iterations. NDI took 87.7 seconds and performed 85 iterations. It is observed that nDi-L1 reconstructs a smaller calcification than NDI, which is closer to the ground truth.
Figure 3 shows the results of the experiment with in-vivo data. The number of iterations was adjusted by visual inspection and the $$$\tau$$$ was adjusted so that the convergence was maximum, point before diverging. nDI-L1 used $$$\tau=0.5$$$ and NDI used $$$\tau=5$$$. nDI-L1 took 169.3 seconds and performed 83 iterations. NDI took 691.8 seconds and performed 500 iterations.
Discussion & Conclusion
The proposed nDI-L1 method shows good performance in qualitative metrics in our experiments. Despite having a worse CalcStreak score than NDI, nDI-L1 more effectivelly suppresed the streaks and achieved a more accurate representation of the calcification (CalcError metric). This might suggest a limitation in the CalcStreak metric. The use of the L1-norm makes non-regularized methods based on gradient descent solvers robust to the generation of streaking artifacts and to noise. nDI-L1 has the quality of performing quick reconstructions saving us the work of fine-tuning regularization parameters, which usually requires multiple reconstructions, which costs a lot of time.Acknowledgements
This work has been funded by projects Fondecyt 1191710, PIA-ACT192064, and the Millennium Nucleus on Cardiovascular Magnetic Resonance of the Millennium Science Initiative NCN17_129, by the National Agency for Research and Development, ANID. Dr Carlos Milovic is supported by Cancer Research UK Multidisciplinary Award C53545/A24348.References
- Polak, D, Chatnuntawech, I, Yoon, J, et al. Nonlinear dipole inversion (NDI) enables robust quantitative susceptibility mapping (QSM). NMR Biomed. 2020;e4271
- Liu T, Wisnieff C, Lou M, Chen W, Spincemaille P, Wang Y. Nonlinear formulation of the magnetic field to source relationship for robust quantitative susceptibility mapping. Magn Reson Med. 2013;69:467-476
- Milovic C, Bilgic B, Zhao B, Acosta-Cabronero J, Tejos C. Fast nonlinear susceptibility inversion with variational regularization. Magn Reson Med. 2018;80:814-821
- Milovic C, Lambert M, Langkammer C, Bredies K, Tejos C, Irarrazaval P. QSM streaking suppression with L1 data fidelity terms . In: Proc. Intl. Soc. Mag. Reson. Med. 2020;p3257.
- Salomir, R., De Senneville, B. D., & Moonen, C. T. W. (2003). A fast calculation method for magnetic field inhomogeneity due to an arbitrary distribution of bulk susceptibility. Concepts in Magnetic Resonance Part B: Magnetic Resonance Engineering, 19(1), 26–34. https://doi.org/10.1002/cmr.b.10083
- Marques, J. P., & Bowtell, R. (2005). Application of a fourier-based method for rapid calculation of field inhomogeneity due to spatial variation of magnetic susceptibility. Concepts in Magnetic Resonance Part B: Magnetic Resonance Engineering, 25(1), 65–78. https://doi.org/10.1002/cmr.b.20034
- Liu T, Spincemaille P, De Rochefort L, Kressler B, Wang Y. Calculation of susceptibility through multiple orientation sampling (COSMOS): a method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in MRI. Magn Reson Med 2009;61:196–204.
- Langkammer C, Schweser F, Shmueli K, et al. Quantitative susceptibility mapping: report from the 2016 reconstruction challenge. Magn Reson Med 2018;79:1661–1673.
- Bilgic, B., Langkammer, C., Marques, J. P., Meineke, J., Milovic, C., & Schweser, F. (pre-print). QSM Reconstruction Challenge 2.0: Design and Report of Results. BioRxiv.
- Marques et al. Part 1. BioRxiv.
- Saiprasad R, Bresler Y. MR image reconstruction from highly undersampled k-space data by dictionary learning. IEEE Trans Med Imag- ing 2011;30:1028–1041.
- Milovic C, Tejos C, and Irarrazaval P. Structural Similarity Index Metric setup for QSM applications (XSIM). 5th International Workshop on MRI Phase Contrast & Quantitative Susceptibility Mapping, Seoul, Korea, 2019.
- Li W, Wu B, Liu C. Quantitative susceptibility mapping of human brain reflects spatial variation in tissue composition. NeuroImage 2011;55:1645–1656.
- Zhou D, Liu T, Spincemaille P, Wang Y. Background field removal by solving the Laplacian boundary value problem. NMR Biomed. 2014;27:312–319.
- Li W, Wu B, Liu C. Quantitative susceptibility mapping of human brain reflects spatial variation in tissue composition. NeuroImage 2011;55:1645–1656.
Figures

Figure 1: Optimal (RMSE-based) reconstructions of the COSMOS forward simulation.

Figure 2: Optimal (RMSE-based) reconstructions of the QSM Challenge 2.0 SIM2SNR1 dataset.
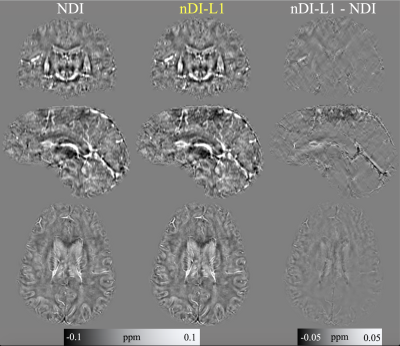
Figure 3: Results in in-vivo data. The optimal number of iterations was selected by visually inspecting the result of each iteration.