3982

Automatic, Non-Regularized Nonlinear Dipole Inversion for Fast and Robust Quantitative Susceptibility Mapping

Carlos Milovic¹ and Karin Shmueli¹
¹Department of Medical Physics and Biomedical Engineering, University College London, London, United Kingdom

Synopsis

Quantitative Susceptibility Mapping (QSM) is an ill-posed inverse problem often solved by regularization: minimizing a functional until it converges. This is usually time-consuming, requiring fine-tuning of several parameters by many repetitions of the whole optimization solver. Nonlinear Dipole Inversion is a QSM method that solves a nonlinear Tikhonov-regularized functional with a gradient descent solver. We show that stopping this method early provides optimal results, largely independent of the regularization weight. Here, we propose a non-regularized nonlinear conjugate gradient solver with a new stopping criterion based on analysing susceptibility map spatial frequency coefficients to achieve fast, parameter-free and automatic QSM.

PURPOSE

Susceptibility maps can be estimated from the phase of Gradient Echo MRI acquisitions by calculating local magnetic field maps and then solving an ill-posed inverse problem. Bayesian approaches to solving the inverse problem rely on minimizing a functional until it converges¹. This is time-consuming and requires fine-tuning of one or more parameters by solving the functional many times. Most functionals are composed of one or more regularization terms which are balanced with a data-fidelity term via a Lagrangian weight ($$$\lambda$$$). For example, the linear QSM functional for Tikhonov regularization is²: $$$argmin_{\chi}\frac{1}{2}||W(F^HDF\chi -\phi)||^2_2+\lambda||\chi||^2_2$$$, with W a magnitude or SNR-based whitening weight, $$$\phi$$$ the local phase, and $$$F$$$ and $$$F^H$$$ the direct and inverse Fourier transforms. D is the dipole kernel in the frequency domain ($$$D=\frac{1}{3}-\frac{k_z^2}{k^2}$$$)^3,4, and $$$\chi$$$ the optimized susceptibility map.
A recent nonlinear gradient descent algorithm (Nonlinear Dipole Inversion, NDI)⁵ gives results comparable to state-of-the-art methods such as MEDI⁶ and FANSI⁷ and largely independent of the regularization weight. By stopping the NDI algorithm early, before it diverges from the true solution, it is possible to avoid the use of a regularization term entirely^5,8. In this paradigm, the number of iterations becomes the main parameter that controls the results. Unfortunately, the gradient descent algorithm used in NDI typically requires hundreds of iterations (albeit each taking a fraction of a second) to achieve optimal results. More problematically, manual supervision is currently needed to stop NDI early as there are no automatic methods available to reliably stop the gradient descent algorithm. Here, we propose an efficient nonlinear conjugate gradient method⁸ to achieve optimal results in much fewer iterations than the gradient descent method. Furthermore, we show that by analyzing the spatial frequency coefficients⁹ of the susceptibility map reconstructed at each iteration, a heuristic rule can be determined to stop the algorithm before noise is amplified, thus preventing streaking artifacts in the final susceptibility map.

METHODS

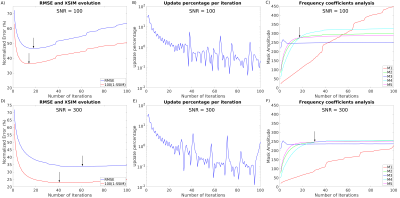
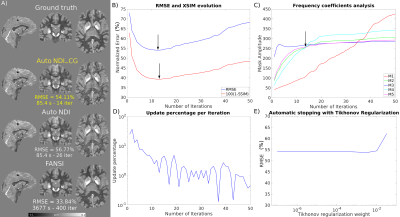
We aimed to solve the nonlinear Quantitative Susceptility Mapping (QSM) functional $$$argmin_{\chi}\frac{1}{2}||W(e^{iF^HDF\chi }-e^{i\phi})||^2_2$$$ with a nonlinear conjugate gradient solver. Exploiting the way that each iteration affects the solutions in the frequency domain⁹ (Figure 1), we analyzed this domain to determine the optimal number of iterations. We propose to use two new frequency masks ($$$M4: 0.15<|D|<0.20$$$ and $$$M5: 0.225<|D|<0.275$$$, with D the dipole kernel coefficients^3,4) to stop the solver when the mean absolute value of the susceptibility map frequency coefficients inside M4 is larger than in M5.
Two benchmark, synthetic brain datasets^10,11 were used to compare the gradient descent (NDI, original formulation⁵) and nonlinear conjugate gradient (NDI_CG) algorithms ,both with automatic stopping, against state-of-the-art nonlinear total-variation (TV)-regularized FANSI⁷. Noisy local phase maps were simulated using the forward model^3,4 from two numerical susceptibility phantoms: 1) A COSMOS reconstruction from the 2016 QSM challenge (RC1)¹⁰ (with SNR=100 and 300) and 2) The 2019 QSM challenge SIM2SNR1¹¹ dataset (RC2). For RC2, the FOV was doubled in every direction to prevent large-scale aliasing for all algorithms (final matrix size: 328x410x410). Reconstructions were compared in terms of normalized root mean squared error (RMSE), QSM-tuned structural similarity index (XSIM)¹², computation time (i7-9750H @4.5GHz with 32Gb RAM), and the number of iterations. All reconstruction strategies were also tested on a challenging 3T in-vivo head and neck dataset¹³: 1.25 mm isotropic voxels, 4 echoes TE / dTE / TR = 4.61 ms / 4.61 ms / 22 ms , α = 12°, Tacq = 6 min 4s. Preprocessing included magnitude-thresholded masking, SEGUE¹⁴ unwrapping and MSHARP¹⁵ background field removal.

RESULTS

Figures 2 and 3 show the results using the RC1 simulations. At each noise level, the optimal number of iterations according to the minimum RMSE and maximum XSIM is very similar to the number of iterations at the intersection of the M4 and M5 amplitude curves where NDI_CG is stopped. Reconstructions using RC2 (Figure 4) also show the same agreement. The update percentage between iterations ($$$100(||\chi_k-\chi_{k-1}||)/||\chi_k||$$$ where $$$\chi_k$$$ is the susceptibility estimated at iteration k) was not a good indicator of the optimal number of iterations. Inserting a Tikhonov regularization term did not improve the RMSE for automatic NDI_CG (Figure 4E). Optimal reconstructions of the in-vivo dataset (Figure 5) show that automatic NDI_CG gives very similar susceptibility maps to NDI.

DISCUSSION

The automatically stopped NDI_CG solver was much faster than traditional NDI, providing similar QSM RMSE/XSIM. Automatic NDI_CG is also faster than FANSI, particularly for large datasets. Both NDI methods gave worse RMSE than FANSI because no denoising is performed in NDI. Our automatic stopping criterion removes the need for time-consuming manual or L-curve-based optimization. In vivo, stopping the NDI_CG algorithm early gave no discernible susceptibility underestimation. This fast, automatic technique may be used in the future to accelerate regularized QSM by initialization or preconditioning¹⁶, or to find optimal regularization weights such as in bi-level approaches¹⁷.

CONCLUSION

We have shown that it is possible to use a non-regularized nonlinear dipole inversion algorithm with an automatic stopping criterion, based on the analysis of susceptibility map frequency coefficients, to achieve a fast, parameter-free QSM reconstruction. In conjunction with a conjugate gradient solver, this provides a fast and robust estimation of susceptibility maps that reduces artifact propagation and noise amplification.

Acknowledgements

Dr Carlos Milovic is supported by Cancer Research UK Multidisciplinary Award C53545/A24348. Dr Karin Shmueli is supported by European Research Council Consolidator Grant DiSCo MRI SFN 770939. We thank Dr. Anita Karsa for her MRI data and contributions.

References

1. Kee Y, Liu Z, Zhou L, Dimov A, Cho J, de Rochefort L, Seo JK, Wang Y. Quantitative Susceptibility Mapping (QSM) Algorithms: Mathematical Rationale and Computational Implementations. IEEE Trans Biomed Eng. 2017;64:2531-2545;

2. Kressler B, Rochefort L De. Nonlinear regularization for per voxel estimation of magnetic susceptibility distributions from MRI field maps. IEEE Trans Med Imaging 2010;29:273–281;

3. Salomir R, De Senneville BD, Moonen CTW. A fast calculation method for magnetic field inhomogeneity due to an arbitrary distribution of bulk susceptibility. Concepts Magn Reson. 2003;19B:26-34

4. Marques J P, Bowtell R. Application of a Fourier-based method for rapid calculation of field inhomogeneity due to spatial variation of magnetic susceptibility. Concepts Magn Reson Part B Magn Reson Eng. 2005;25:65-78

5. Polak, D, Chatnuntawech, I, Yoon, J, et al. Nonlinear dipole inversion (NDI) enables robust quantitative susceptibility mapping (QSM). NMR Biomed. 2020;e4271

6. Liu T, Wisnieff C, Lou M, Chen W, Spincemaille P, Wang Y. Nonlinear formulation of the magnetic field to source relationship for robust quantitative susceptibility mapping. Magn Reson Med. 2013;69:467-476

7. Milovic C, Bilgic B, Zhao B, Acosta-Cabronero J, Tejos C. Fast nonlinear susceptibility inversion with variational regularization. Magn Reson Med. 2018;80:814-821

8. Milovic C, Karsa A, and Shmueli K. Efficient Early Stopping algorithm for Quantitative Susceptibility Mapping (QSM). ESMRMB 2020, Virtual Meeting.

9. Milovic C,Prieto C, Bilgic B, Uribe S, Acosta-Cabronero J, Irarrazaval P, Tejos T. Comparison of Parameter Optimization Methods for Quantitative Susceptibility Mapping. Magn Reson Med. 2020;85:480– 494

10. Langkammer C, Schweser F, Shmueli K, Kames C, Li X, Guo L, Milovic C, Kim J, Wei H, Bredies K, Buch S, Guo Y, Liu Z, Meineke J, Rauscher A, Marques JP, Bilgic B. Quantitative susceptibility mapping: Report from the 2016 reconstruction challenge. Magn Reson Med. 2018;79:1661-1673

11. Marques JP, Meineke J, Milovic C, Bilgic B, Chan K-S, Hedouin R, van der Zwaag W, Langkammer C, and Schweser F. QSM Reconstruction Challenge 2.0–Part 1: A Realistic in silico Head Phantom for MRI data simulation and evaluation of susceptibility mapping procedures. bioRxiv 2020.09.29.316836; doi: https://doi.org/10.1101/2020.09.29.316836

12. Milovic C, Tejos C, and Irarrazaval P. Structural Similarity Index Metric setup for QSM applications (XSIM). 5th International Workshop on MRI Phase Contrast & Quantitative Susceptibility Mapping, Seoul, Korea, 2019

13. Karsa A, Punwani S, and Shmueli K. An optimized and highly repeatable MRI acquisition and processing pipeline for quantitative susceptibility mapping in the head-and-neck region. Magn Reson Med. 2020; 84: 3206– 3222

14. Karsa A, Shmueli K. SEGUE: A Speedy rEgion-Growing Algorithm for Unwrapping Estimated Phase. IEEE Trans Med Imaging. 2019;38:1347-1357

15. Milovic C, Langkammer C, Uribe S, Irarrazaval P, Acosta-Cabronero J, and Tejos C. Multiscale Spherical Mean Value based background field removal method for Quantitative Susceptibility Mapping. 27th International Conference of the ISMRM, Montreal, Canada, 2019.

16. Liu Z, Kee Y, Zhou D, Wang Y, Spincemaille P. Preconditioned total field inversion (TFI) method for quantitative susceptibility mapping. Magn Reson Med. 2017;78:303-315

17. De los Reyes JC, Schönlieb CB. and Valkonen T. Bilevel Parameter Learning for Higher-Order Total Variation Regularisation Models. J Math Imaging Vis 2017;57:1–25

Figures

Figure 1: Spatial frequency components of the RC1 ground truth and NDI_CG reconstructions for different numbers of iterations. With more iterations, frequencies close to the magic angle are amplified. To assess QSM optimality (RMSE: 18 iterations), the mean absolute values of the frequency coefficients in regions M1-M3 have been used previously8. Here, regions M4 and M5 near the cone were used. All regions were defined as a function of the dipole kernel coefficients and radial frequencies 0.60-0.95 mm-1.

Figure 2: Quantitative evaluations of reconstructions of the RC1 simulations, for SNR= 100 (top) and 300 (bottom). The optimal numbers of iterations according to minimum RMSE / maximum XSIM agree well with those defined by the intersection of the mean absolute amplitudes inside masks M4 and M5 (arrows). For high SNR data, the algorithm diverges slowly making this selection less critical. No relationship was found between the optimal number of iterations and the update convergence.

Figure 3: Comparison of RMSE-optimal NDI_CG and FANSI reconstructions of the RC1 phantom with automatically stopped NDI and automatically stopped NDI_CG. AutomaticNDI_CG is much faster than FANSI but produces worse RMSE due to the lack of noise reduction steps. Automatically stopped NDI achieves slightly better RMSE than automatically stopped NDI_CG since the step size in gradient descent is typically smaller. Otherwise these results are equivalent, and very similar to RMSE-optimal NDI_CG.

Figure 4: Comparison of optimal reconstructions for the RC2 phantom. NDI reconstructions show more streaking than FANSI but are ~40 times faster. FANSI parameter optimization took several hours. The optimal number of iterations from RMSE/XSIM curves agrees with the number of iterations at the intersection of the M4 and M5 amplitude curves (arrows). Additional experimentation with a Tikhonov regularization term in the NDI_CG solver showed no change in RMSE over a wide range of regularization weights.

Figure 5: Comparison of Auto NDI_CG and Automatically stopped NDI with FANSI in vivo. High quality NDI reconstructions are possible even with extremely noisy voxels. Auto NDI_CG and Auto NDI produce very similar susceptibility maps (with substancial control of streaking artifacts and sharp fine details) but NDI_CG is much faster and showed no signs of susceptibility underestimation.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

3982