Introduction

Nonlinear Dipole Inversion¹ (NDI) solves the nonlinear formulation of the dipole inversion in QSM by using gradient descent iterations and the analytic gradient of the cost function to solve the ill-posed minimization problem. NDI regularizes implicitly by early exit. With only one tunable parameter, the number of iterations, NDI presents an effective method for solving the nonlinear ill-posed inversion. Here we extend NDI by solving the nonlinear minimization problem using a second order method. The nonlinear formulation of the dipole inversion for mapping magnetic susceptibility from local field measurements minimizes: $$f(\chi)=||W(e^{iD\chi}–e^{i\varphi})||_2^2$$, where χ is the magnetic susceptibility, W a weighting matrix traditionally derived from the magnitude image, D the dipole kernel convolution matrix, and φ the local field. NDI solves Equation [1] using gradient descent: $$\chi_{k+1}=\chi_k-\tau \nabla f(\chi_k)$$ The gradient of f(χ) is computed analytically as $$\nabla f(\chi)=2D^*W^*W \text{sin}(D\chi -\varphi)$$. Although simple and numerically efficient the iterations given by Equation [1] converge only linearly with n, as only the gradient is used in performing the minimization. Even with an early stopping criterion, many iterations are required. However, by incorporating the Hessian of f, second order methods, such as quasi-Newton methods, can drastically improve convergence. The quasi-Newton iteration scheme is given by: $$\chi_{k+1}=\chi_k -\tau B(\chi_k)^{-1}\nabla f(\chi_k)$$, where B(χ) is an approximation of the Hessian of f . While we can compute the analytic Hessian of [1] to use in Equation [3], which gives Newton's method, it is too computationally expensive to invert. However, the diagonal of the Hessian given by $$B(\chi) = 2D^*D^*W^*W\text{cos}(D\chi - \varphi)$$ is trivial to invert and the iteration scheme becomes: $$\chi_{k+1}=\chi_k -\tau \frac{2D^*W^*W\text{sin}(D\chi_k -\varphi)}{|2D^*D^*W^*W\text{cos}(D\chi -\varphi)|+\mu}$$, where μ is a parameter to deal with regions of small curvature and we take the absolute value of the Hessian to deal with negative curvature. We set μ to $$$\sqrt{\text{max}|\nabla f(\chi_k)|}$$$. We use a fixed step size of τ=1 for all iterations as we found that a line search does not improve convergence speed. Similar to NDI we can improve HANDI by introducing data-driven non-linear regularizers. Here, we propose HANDINet, which is a type of variational network. HANDINet uses unrolled proximal Newton-type iterations $$\chi_{k+1}=\chi_k -\tau \text{prox}(\chi_k–B(\chi_k)^{-1}\nabla f(\chi_k))$$ to learn the proximal operator of the regularizer.

Results

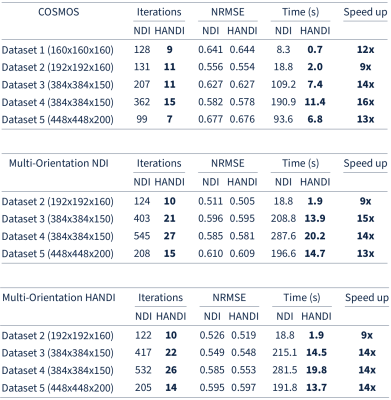
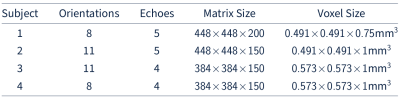
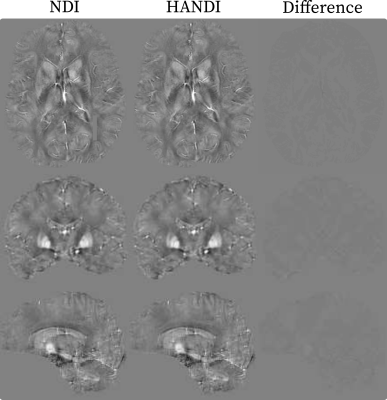
We investigate the convergence rate of HANDI for five different datasets: 1) the dataset from the 2016 QSM reconstruction challenge² (matrix size=160x160x160) , 2) the dataset provided from the NDI study³ (matrix size=192x192x160), and 3) three datasets acquired at our research centre (matrix sizes=384x384x150 and 448x448x200). Each dataset features a different acquisition protocol, voxel sizes, matrix size, and pre-processing steps. Since both NDI and HANDI use the iteration number as regularization parameter, we compared the solution at each iteration with the datasets' multi-orientation reference to find the iteration number that resulted in the lowest normalized root-mean-square-error (NRMSE). The results are summarized in Table 1. For all datasets HANDI requires fewer iterations resulting in 10x faster reconstruction than NDI, while the NRMSE values are the same as for NDI. A reconstructed susceptibility map from both methods is shown in Figure 1. As expected from the error values, the susceptibility maps look almost identical . To evaluate the efficacy of the proposed proximal Netwon-type network we trained HANDINet and compared it to a variational network based on unrolled NDI iterations and a variational network based on the standard linear deconvolution problem formulation. All three networks were trained from scratch and used 8 unrolled iterations. The learned regularizers were parameterized using the same network architecture. The architecture used is an adaptation of the one proposed by Myronenko⁴, and differs in the initial number of filters (8 instead of 32) and does not include the VAE branch. Training and testing data was acquired from 4 healthy volunteers, 12 multiple-echo scans at varying orientations per volunteer, on a Philips Achieva 3T scanner. The scan parameters are summarized in Table 2. 116 3D images were used for training, 21 for testing. Laplacian unwrapping and v-SHARP was performed. COSMOS was used as reference. All networks were trained on 112x112x64 patches, using Adam with an initial learning rate of 1e-4 and batch size 8, and l1 loss . Table 3 shows the mean NRMSE of the test dataset for all three networks. HANDINet achieves the lowest reconstruction error. Surprisingly, the variational network based on the standard deconvolution results in lower NRMSEs than the variational NDI.

Discussion and Conclusion

We extended a first order nonlinear dipole inversion method by incorporating the diagonal of the Hessian, which can be found analytically, to derive a second order, quasi-Newton method. HANDI, as well as NDI, does not include an explicit regularization parameter but regularizes the ill-posed minimization by exiting the iterative scheme early. As exiting early is a robust regularization technique commonly used in QSM^5,6, the robustness of which is further shown in this study, it is more desirable than explicit regularization strategies. The proposed learned proximal Newton method, which is based on unrolled HANDI iterations, further improves reconstruction accuracy compared to COSMOS and outperforms similar variational networks using unrolled NDI and standard dipole deconvolution iterations. HANDINet is able to combine the expressiveness of deep learning and the increased convergence rate of second order methods.

Acknowledgements

Natural Sciences and Engineering Research Council of Canada, Grant/Award Number 016-05371, the Canadian Institutes of Health Research, Grant Number RN382474-418628, the National MS Society (RG-1507-05301). A.R. is supported by Canada Research Chairs 950-230363.