Introduction

In recent years, a number of studies have suggested to use deep neural networks for dipole inversion of QSM reconstruction^1–6. These studies have shown improved results compared to conventional methods. However, only few studies performed comparison between a newly proposed network and a previously published network. Furthermore, the comparison was often done under different conditions (e.g. comparison of two networks trained by different training datasets), making it difficult to assess the results. Recently, a study reported that the deep neural networks for dipole inversion have generalization issues including the type of the training dataset (e.g. simulated data vs in-vivo data), severely influencing the performance of the network⁷. Currently, most studies utilized their own dataset for network training, making the claims of a “better” network than the previous ones untrustworthy. In this study, we demonstrated that at least two conditions are required for a fair comparison between networks for dipole inversion: First, test data need to have the same characteristics as training data. Second, hyperparameter tuning should be performed if training dataset is changed. Our study implies that a common dataset is necessary for a fair comparison of deep neural networks for QSM.

Methods

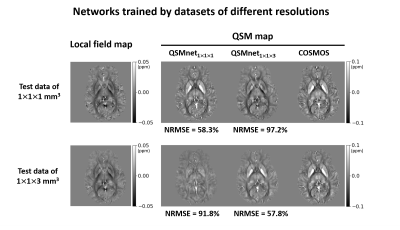
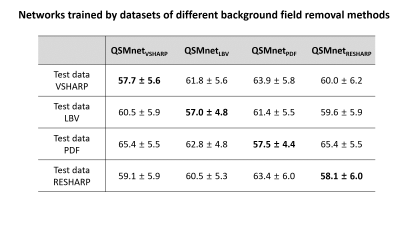
First, we demonstrated that the comparison results between networks depend on whether the characteristics of test data are the same as those of training data. Two neural networks, QSMnet_1×1×1 and QSMnet_1×1×3, were trained by two training datasets that differ only in resolutions (1×1×1 mm³ and 1×1×3 mm³). The 1×1×1 mm³ resolution dataset was the same as the reference³ and the 1×1×3 mm³ resolution dataset was generated by truncating k-space from the 1×1×1 mm³ resolution dataset. The training was stopped at 50 epochs in QSMnet_1×1×1 and 150 epochs in QSMnet_1×1×3, and the other training details were the same as the reference³. The best network was chosen to have the minimum L2 loss in the validation set. QSMnet_1×1×1 and QSMnet_1×1×3 were compared on two test datasets that differ only in the resolution. The NRMSE was measured in the reconstructed QSM map of each network with the COSMOS QSM map as a reference.
In the second experiment, we tested the effects of background field removal methods in the datasets. Four networks, QSMnet_VSHARP, QSMnet_LBV, QSMnet_PDF, and QSMnet_RESHARP, were trained respectively by four training datasets using different background field removal methods. The experimental details were the same as the first experiment. A pairwise t-test with Bonferroni correction was conducted for each test data between the best performance and the other three performances.
Finally, the need for hyperparameter tuning was tested when the training dataset is changed. The hyperparameters of the original QSMnet were empirically determined for the 1x1x1 mm³ training dataset. When the same network was trained with a new (1×1×3 mm³) resolution, its performance may not be optimum, requiring hyperparameter tuning. Two networks, one (QSMnet_1×1×3-ref) with hyperparameters from the reference³ and the other (QSMnet_{1×1×3-hyper}) with newly optimized hyperparameters for the new dataset were compared. The hyperparameter optimization was performed through a random search, and the best hyperparameter set was chosen to have the minimum L2 loss in the validation set. These networks were evaluated in the test dataset of the same resolution as the training dataset. The NRMSE was measured in the reconstructed QSM map with the COSMOS QSM map as a reference. A pairwise t-test was conducted for statistical analysis.

Results

Figure 1 shows the comparison results of the networks that were trained by different resolution datasets. Both networks yielded better performance when the resolution of the test data was the same as that of the training data. Figure 2 reveals the performance comparison results of QSMnet_VSHARP, QSMnet_LBV, QSMnet_PDF, and QSMnet_RESHARP. Similar to the resolution study, each neural network showed the best performance when the test data and the training data were processed in the same background field removal method. These results confirm that using the same characteristic dataset for training and test is important for a fair comparison of the networks.
Figure 3 shows the performance comparisons between the two hyperparameter sets. The original hyperparameter set from the reference³ (QSMnet_1x1x3-ref) and the optimized hyperparameter set (QSMnet_1x1x3-hyper) have different network structures (neural network layers, activation function, etc) and training methods (batch size, learning rate, etc). The newly optimized QSMnet_1x1x3-hyper resulted in a smaller NRMSE than that of QSMnet_1x1x3-ref (56.6±7.0% vs 57.8±7.1%; p=4.7e-4). The results demonstrate that for the training dataset of different characteristics, the performance of QSMnet can be improved by hyperparameter tuning.

Discussion and Conclusion

In summary, we demonstrated that the comparison results between networks depend on the characteristics of the training/test dataset. Furthermore, we showed that hyperparameter tuning should be performed if training dataset is changed. This finding suggests that even if one utilizes his/her own dataset for the retraining and testing of a published network, the issue of unfair comparison still exists because the network can be re-optimized via hyperparameter tuning. Hence, the claim of a “better” network could be solely from the efforts for tuning. These results imply the necessity of a common dataset for a fair comparison of networks for QSM. As a potential data source, one may access to our dataset at the following link (https://github.com/SNU-LIST/QSMnet).

Acknowledgements

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. NRF-2018R1A2B3008445), and Creative-Pioneering Researchers Program through Seoul National University (SNU).