3958
Multi-scale Accelerated Auto-differentiable Bloch-simulation based joint design of excitation RF and gradient waveforms.
Tianrui Luo1, Douglas C. Noll1, Jeffrey A. Fessler1, and Jon-Fredrik Nielsen1
1University of Michigan, Ann Arbor, MI, United States
1University of Michigan, Ann Arbor, MI, United States
Synopsis
A recently proposed auto-differentiable Bloch simulation approach allows joint design of RF and gradient waveforms for large-tip objectives. However, that approach requires a relatively long design time, preventing online pulse design. As a refinement, we propose to accelerate such simulation-based pulse design approaches by dividing it into two stages: 1) fast coarse dwell time design; 2) fine dwell time tuning. This combination substantially reduced the design time (from 8.5 min to 3 min), while still attaining high excitation accuracy, enabling online pulse design applications.
Introduction
Joint design of excitation RF and gradient waveforms is challenging, as it requires solving the Bloch equation numerically. Conventional approaches for the joint design problem typically rely on the small-tip approximation [1] that assumes constant longitudinal magnetization $$$M_z$$$ throughout the excitation. These approaches assume an approximate Fourier transform relation between the transversal excitation profile and the excitation k-space. The small-tip approximation yields relatively simple expressions of the loss derivatives with respect to both the RF waveform and the k-space trajectory, facilitating optimizing the pulse for a specific excitation goal. However, for large-tip applications, these approaches can be unsatisfactory due to the inapplicable small-tip assumption. Also, their flexibility is limited for adapting to different loss functions, requiring extra derivations and implementations.Recent work [2] proposed an auto-differentiation (AD) based pulse design approach, and a change of variable based method to handle scanner hardware constraints (e.g., RF power, and slew rate limits). Specifically, the work developed an efficient auto-differentiable Bloch simulator plus its explicit Jacobian operation. For arbitrary sub-differentiable excitation objective functions, by simulating the performance of a pulse, the simulator can yield the numerical derivatives with respect to the RF and gradient waveforms for optimization purposes. The work was validated with 3D spatially tailored large-tip pulse designs.
One downside of the method in [2] is the design time that is proportional to the length of the designed pulse due to the method’s required simulations. While being more efficient than implicit Jacobian operations provided by typical AD frameworks, it can still take about 9 min to design a 4.6 ms long 3D inner volume inversion pulse. To accelerate the method in [2], we propose to divide pulse design into two stages: 1) coarse simulation dwell time (20 us) fast design; and 2) fine simulation dwell time (4 us) tuning. We demonstrate that this strategy attains substantially shortened design time (e.g., 3 min), while having negligible excitation performance difference.
Methods
[2] proposed to address general pulse design problems via auto-differentiable Bloch simulation: $$\arg\min_{g, b}\qquad\mathcal{L}(g,b)=f(M_T(g,b), M_D)+\mathcal{R},$$ where $$$b$$$ and $$$g$$$ are the RF and gradient waveforms respectively; loss $$$L$$$ includes excitation error $$$f$$$ and regularization $$$R$$$; $$$f$$$ quantifies the difference between, $$$M_T$$$ and $$$M_D$$$, the simulated and the desired excitation profile; $$$R$$$ can be RF power penalization, etc.This work accelerates the design procedure as follows: 1) Initialize $$$b$$$ and $$$g$$$ using the extended kt-points method [3] with a default dwell time (4 us); 2) Temporally downsample $$$b$$$ and $$$g$$$ to a coarse dwell time (20 us), and optimize using the algorithm described in [2] for 8 iterations; 3) Linearly interpolate the optimized coarse pulse to the fine dwell time 4 us, then optimize the interpolated pulse using 1 iteration of the algorithm in [2] to obtain the final pulse. The coarse dwell time (20 us) is chosen empirically for 4 us hardware dwell time. Dwell time finer than 20 us requires longer design time, and coarser than 20 us yields degraded excitation performance after the two stage design.
We validated this procedure with the OV90 and IV180 objectives described in [2]. The OV90 loss function is defined as [2]: $$\arg\min_{g,b}\qquad\||M_{Dxy}|-|M_T(b,g)_{xy}|\|_2^2+\lambda\|b\|_2^2,$$ where $$$M_{Dxy}$$$ and $$$M_T(b,g)_{xy}$$$ are the desired and Bloch simulated transverse magnetizations, respectively; $$$\lambda \|b\|_2^2$$$ regularizes the RF power. OV90 is a magnitude least square excitation task with a goal of exciting only the complement of a 3D cuboidal inner volume (IV), i.e., the outer volume (OV).
The IV180 loss function is defined as [2]: $$\arg\min_{g,b}\qquad\||M_{Dz}|-|M_T(b,g)_z|\|_2^2+\lambda\|b\|_2^2,$$ where $$$M_{Dz}$$$ and $$$M_T(b,g)_z$$$ are the desired and Bloch simulated longitudinal magnetizations, respectively. IV180 is an inversion task with a goal of inverting the spins inside a 3D cuboidal IV while leaving the OV untouched.
Figure 1 shows the acquired off-resonance map used in the pulse design, and the cubic shape of IV and OV. We present simulation studies comparing the performances of our proposed acceleration strategy and that of the method in [2].
Results
Figures 2 and 3 show the comparison of the OV90 objective. We observe that our proposed pulse design is much faster than the method in [2], (3 min vs 8.5 min), and also obtains a better excitation profile (NRMSE: 4.3% vs 4.6%). Figure 4 and 5 shows the comparison regarding the IV180 objective. Again, our proposed method is much faster than [2], (3.5 min vs 10.5 min), while the excitation profile is slightly worse (NRMSE: 7.98% vs 7.65%).Discussion and Conclusion
We have presented an acceleration strategy for auto-differentiable simulation based joint pulse design. The strategy substantially reduces the design time while maintaining a decent excitation accuracy for 3D spatially selective large-tip excitation objectives. This design time improvement can make the AD pulse design approach practical for routine human scanning. Our pulse design approach is general and not limited to a particular excitation objective. We expect this approach to find use in other pulse design applications, such as parallel transmit excitation pulses.Acknowledgements
This work is supported in part by NIH Grants R21 AG061839, R01 EB023618, and U01 EB026977, and NSF Grant IIS 1838179.References
- Pauly, John, Dwight Nishimura, and Albert Macovski. "A k-space analysis of small-tip-angle excitation." Journal of Magnetic Resonance (1969) 81.1 (1989): 43-56.
- Luo, Tianrui, et al. "Joint Design of RF and gradient waveforms via auto-differentiation for 3D tailored excitation in MRI." arXiv preprint arXiv:2008.10594 (2020). https://arxiv.org/abs/2008.10594
- Sun, Hao, et al. "Joint design of excitation k-space trajectory and RF pulse for small-tip 3D tailored excitation in MRI." IEEE Transactions on Medical Imaging 2016; 35(2): 468-479.
Figures
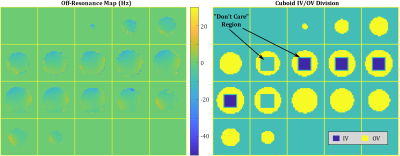
Off-resonance map (left), and division of IV and OV (right). A “Don’t Care” region is prescribed to exclude the boundary between IV and OV from excitation error computation, allowing smooth transitions of spin states after the excitation.
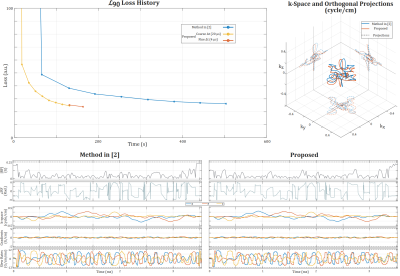
Comparison of designs on outer volume excitation objective (OV90). Our proposed method is much faster than the method in [2] (3 min vs 8.5 min). The optimized pulse waveforms and the k-space trajectory resemble that of method [2].
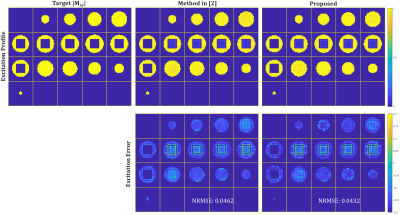
Comparison of simulated excitation profiles for the pulses in Fig. 2. The goal is to excite only the spins in the outer volume. In terms of NRMSE, our proposed method performance is slightly better than that of method [2].

Comparison of designs on outer volume excitation objective (IV180). Our proposed method is much faster than the method in [2] (3.5 min vs 10.5 min). This design takes longer than that for the OV90 objective, as the pulse is longer than the OV90 pulse. The optimized pulse waveforms and the k-space trajectory resemble that of method [2].
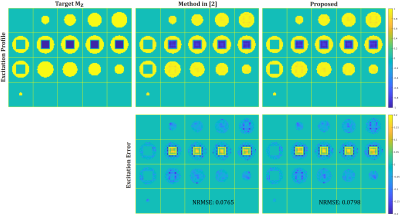
Comparison of simulated inversion profiles for the pulses in Fig. 4. The goal is to invert only the spins in the inner volume. In terms of NRMSE, our proposed method performance is slightly worse than that of method [2].